Épistémique vs. ontiques
En mécanique quantique, l’évolution d’un système isolé est unitaire, c’est‑à‑dire décrite par un opérateur qui conserve la norme (ou la probabilité totale) du vecteur d’état ; cette dynamique, entièrement déterministe, est gouvernée par l’équation de Schrödinger. Dès qu’une mesure intervient, toutefois, la règle de Born (postulat de projection) impose une seconde loi : l’état s’effondre de façon non unitaire et aléatoire pour livrer l’un des résultats possibles, puis se fige afin que le même résultat soit retrouvé si l’on répète immédiatement la mesure. Malgré ce clivage, ce cadre théorique a révolutionné notre compréhension du monde et propulsé des avancées technologiques spectaculaires1.
Réconcilier ces deux modes d’évolution — l’un continu, réversible et probabilistiquement conservatif, l’autre discontinu, irréversible et intrinsèquement stochastique — reste l’un des défis conceptuels majeurs de la physique moderne. C’est le problème de la mesure. D’ailleurs, la simple question “C’est quoi mesurer un système ?” n’a pas à ce jour de réponse claire, loin de là.
Distinction de Harrigan et Spekkens
Une partie de la communauté scientifique a adopté une attitude d’esquive en décrétant que l’appareil théorique n’est qu’une machinerie performante pour prédire les résultats des expériences, rien de plus. Le reste n’est que balivernes philosophiques. Cette approche instrumentiste n’attribue dès lors aucune réalité à l’état quantique.
Les instrumentistes font partie du camp ψ-épistémique pour lesquels l’état quantique ψ n’est que porteur d’information sans réalité physique. Ils se sont très tôt réunis dans l’“école de Copenhague” qui a longtemps servi de canon à l’enseignement de la quantique. Leur mantra un peu caricatural est le célèbre “shut up and calculate”.
De l’autre côté du spectre, on a les interprétations ψ-ontiques pour lesquelles l’état quantique traduit une réalité physique.
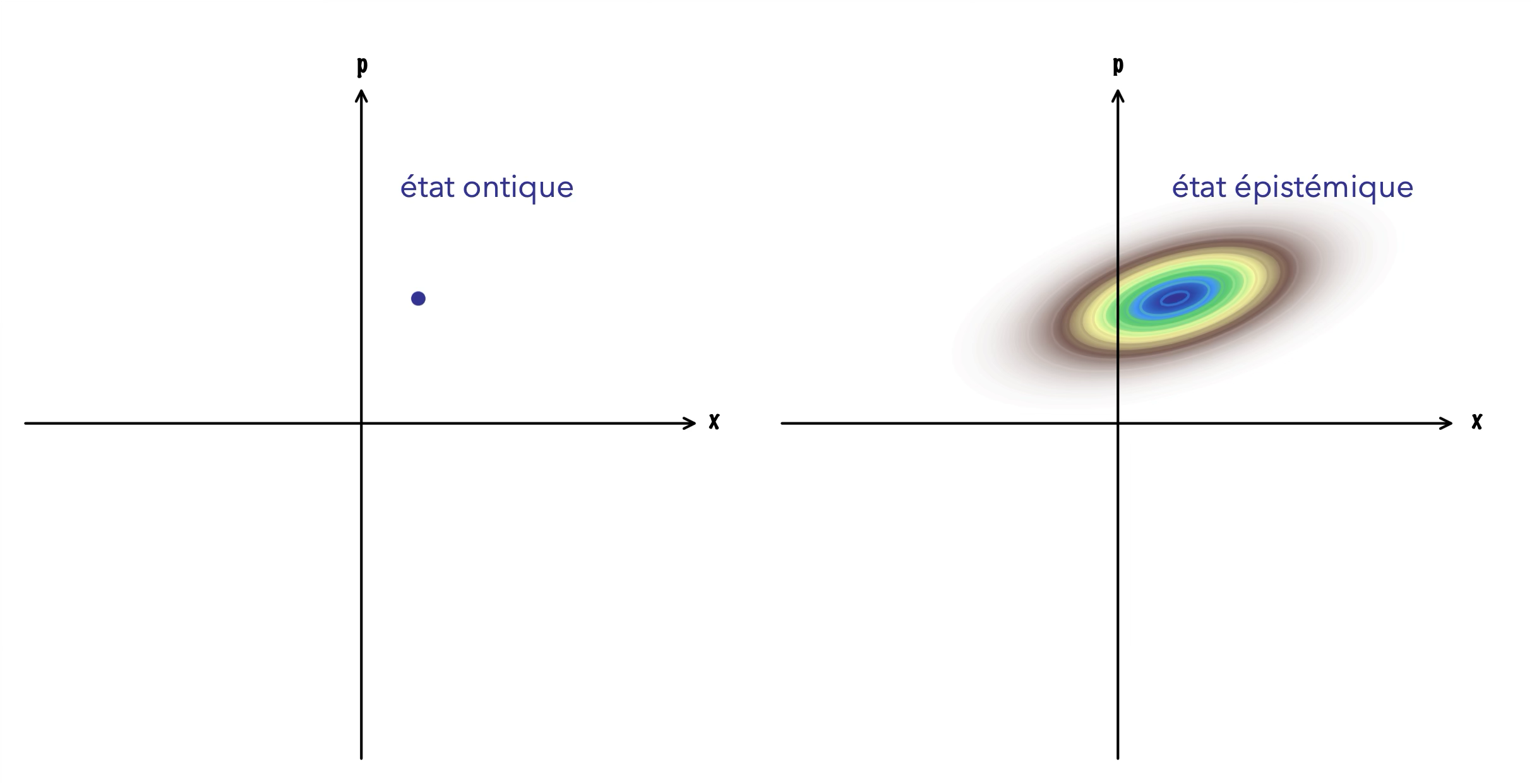
Il y a malgré tout des ψ‑épistémiques moins hardcores qui imaginent une réalité cachée derrière l’état quantique. L’état quantique représente alors notre connaissance (incomplète) de cette réalité de la même façon qu’une distribution de probabilité dans l’espace des phases représente notre connaissance de la position ponctuelle d’une particule. Le modèle jouet de Spekkens illustre ça très bien.
Supposons qu’une théorie ou modèle associe au système une propriété physique $\lambda$ (la réalité) qui détermine la probabilité des différents résultats obtenus lors de la mesure du système.
La théorie quantique va, elle, associer un état quantique $|\psi\rangle$ à un système préparé d’une certaine façon. Mais l’état physique $\lambda$ n’est pas nécessairement fixé de manière unique par la préparation qui a produit $|\psi\rangle$. On dira que la préparation a produit un état physique $\lambda$ selon une distribution de probabilité $\mu_\psi(\lambda)$.
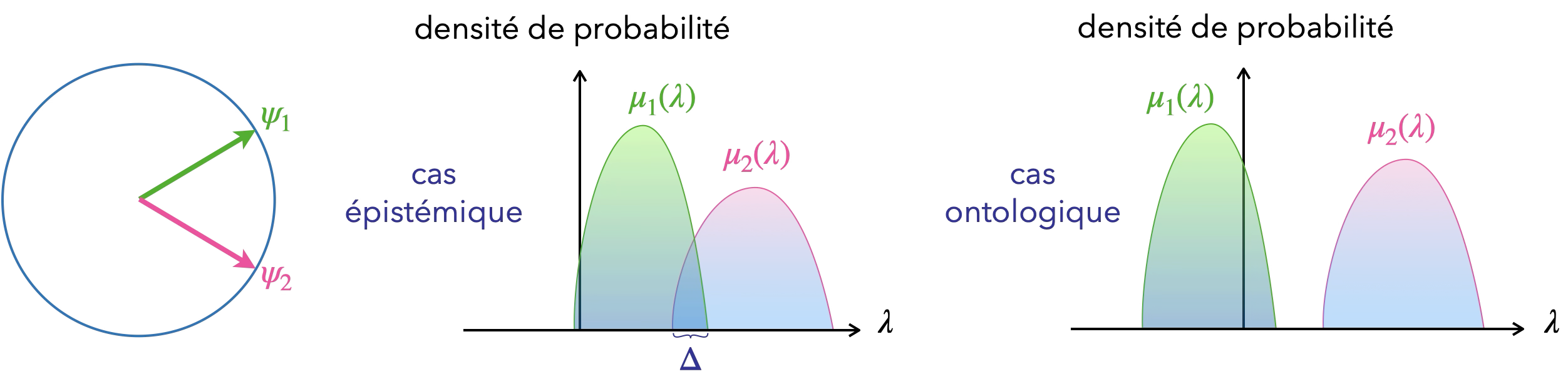
Supposons maintenant que pour toute paire d’états quantiques $|\psi_1\rangle$ et $|\psi_2\rangle$, les distributions $\mu_1(\lambda)$ et $\mu_2(\lambda)$ ne se recouvrent jamais. L’état quantique $|\psi\rangle$ peut alors être inféré de manière unique à partir de l’état physique du système. Ça définit bien au final une “propriété physique” pour l’état quantique (puisqu’il y a une correspondance un pour un entre état quantique et propriété physique $\lambda\leftrightarrow\psi$). C’est la vision ψ-ontique.
À l’inverse, s’il y a recouvrement pour au moins une paire d’états quantiques, alors $|\psi\rangle$ peut être vu que comme un simple porteur d’information sans réalité. Comment l’état quantique pourrait être l’incarnation d’une réalité si la même réalité physique peut se cacher derrière différents états quantiques ? C’est bien la possibilité même du chevauchement qui rend un ψ‑épistémique ψ‑épistémique (où serait l’incertitude sans cela ?).
Cette distinction entre état épistémique et état ontique reposant sur le non‑recouvrement a été développée par Harrigan et Spekkens dans un article de 2010 :
Harrigan, N. & Spekkens, R. W. “Einstein, Incompleteness, and the Epistemic View of Quantum States”, Foundations of Physics 40 (2), 125–157 (février 2010) 🌐
Attraits de la vision ψ-épistémique
Tous les ψ‑épistémiques s’accordent sur le statut probabiliste de la fonction d’onde. Comme dans le modèle jouet de Spekkens, ce point de vue permet de démystifier certaines bizarreries quantiques et c’est une approche de ce type que j’utilise dans la vidéo ci-dessous pour tenter de rendre plus accessible l’état quantique.
Un argument fort pour cette vision probabiliste de la fonction d’onde est justement le fait que la théorie quantique peut être considérée comme une généralisation non commutative de la théorie classique des probabilités comme l’a montré von Neumann.
Mais un argument à mes yeux bien plus convaincant pour la ψ-épistémologie est la dissolution qu’elle entraîne du problème de la mesure. Rappelons-nous que le problème nait de la double règle d’évolution du formalisme quantique : l’une douce et continue lorsque le système est isolé et non observé et l’autre instantanée et discontinue lors d’une mesure. Comme une mesure n’est théoriquement qu’une interaction physique, on peut se demander pourquoi elle ne pourrait pas être modélisée par l’équation de Schrödinger. Mais c’est en suivant cette voie qu’on se retrouve avec des situations apparemment absurdes comme celle du chat mort et vivant.

Le problème ne se pose en fait que pour des états ψ-ontiques ; seulement alors se retrouve-t-on avec un chat réellement dans deux états superposés. Pour un ψ‑épistémique, la fonction d’onde n’a jamais représenté que l’étendue de nos connaissances, le chat peut très bien être mort ou vivant avant qu’on regarde. La description par une superposition ne reflète que notre ignorance de la possibilité qui s’est réalisée. L’étendue de la fonction d’onde dans l’espace des phases n’est pour un ψ‑épistémique qu’un brouillard d’incertitude.
Théorème PBR et nécessité de l’ontologie
Les ψ-ontiques associent, eux, une réalité à la fonction d’onde. On peut les classer en deux catégories (en appelant $\lambda$ la propriété physique associée au système, cf. plus haut) :
-
les purs et durs pour lesquels la fonction d’onde est la réalité fondamentale ($\lambda\equiv\psi$),
-
et ceux qui supplémentent $\psi$ avec des variables additionnelles $\xi$ ($\lambda=(\psi,\xi)$).
A priori, les ψ-ontistes n’ont pas grand-chose pour eux ; le problème de la mesure redevient un problème sérieux, la fonction d’onde vit dans un espace à grande dimension, les inégalités de Bell imposent une non localité des variables cachées et le théorème de Kochen‑Specker impose leur contextualité. Pour les ψ-ontistes purs et durs, c’est moins compliqué à avaler puisqu’ils ont signé en connaissance de cause (la quantique est non locale et contextuelle), mais pour ceux qui espéraient cacher des propriétés plus sympathiques dans $\xi$, c’est râpé.
Les ψ‑ontiques devaient passer pour de sacrés masos aux yeux des ψ‑épistémiques jusqu’au jour où le théorème PBR leur est tombé dessus.
Pusey, M. F. ; Barrett, J. ; Rudolph, T. (2012). “On the reality of the quantum state”. Nature Physics. 8 (6): 475–478 🌐
Revenons à la distinction entre ψ‑ontiques et ψ‑épistémiques résumée par ce schéma :

Les trois physiciens Pusey, Barrett et Rudolph ont réussi à montrer que si les distributions de probabilité d’une propriété physique (ontologiques) se recouvrent ($\mu_1(\lambda)\cdot\mu_2(\lambda)=q>0$) pour deux états quantiques distincts $|\psi_1\rangle$ et $|\psi_2\rangle$ (plus précisément si la mesure de l’intersection $\Delta$ des supports n’est pas nulle), alors il y a une contradiction avec les prédictions de la théorie quantique.
PBR est donc un no-go theorem. Pour des hypothèses somme-toute assez raisonnables, il prouve qu’une interprétation épistémique de la fonction d’onde n’est pas compatible avec des propriétés physiques réelles2.
Il aurait suffit pour prouver que $|\psi\rangle$ est épistémique de trouver une seule paire d’états dont les densités de probabilité se recouvrent alors que pour prouver qu’il est ontique, il faut s’assurer que c’est le cas d’aucune paire… Mais c’est bien ce que PBR a réussi à faire !
L’absence de recouvrement quand les deux états quantiques sont orthogonaux n’est pas vraiment surprenante. Par contre, le fait que cela tienne pour des états non orthogonaux est plus troublant ($\mu_1(\lambda) \mu_2(\lambda)=0$ pour tout $\lambda$ même si $\left\langle\psi_1 \mid \psi_2\right\rangle \neq 0$).
Pourquoi c’est étonnant ?
Si on a $\left\langle\psi_1 \mid \psi_2\right\rangle \neq 0$, on obtient en introduisant la résolution de l’identité pour une base quelconque de l’espace ($1=\int \mathrm{d} a|a\rangle\langle a|$) $\int \mathrm{d} a\left\langle\psi_1 \mid a\right\rangle\left\langle a \mid \psi_2\right\rangle \neq 0 $. Donc pour au moins un $a$, $\left\langle\psi_1 \mid a\right\rangle\left\langle a \mid \psi_2\right\rangle \neq 0$. Et comme $\rho_i(a)=\left|\left\langle a \mid \psi_i\right\rangle\right|^2$, ça donne finalement $\rho_1(a) \rho_2(a) \neq 0$ pour au moins un $a$.
Moralité : les distributions de probabilités quantiques se recouvrent sans que cela ne soit le cas des distributions de $\lambda$ !
► Idée de la preuve de PBR :
Brossons la preuve sur l’exemple d’une paire d’états non orthogonaux (PBR le généralise à une paire arbitraire).
Supposons un espace de Hilbert à 2 dimensions avec une base orthogonale $|0\rangle$, $|1\rangle$.
Et soit une autre base orthogonale $|+\rangle$, $|-\rangle$, avec $|\pm\rangle=\frac{|0\rangle \pm |1\rangle}{\sqrt{2}}$.
Prenons la paire non orthogonale $|0\rangle$, $|+\rangle$ ($\langle 0 \mid+\rangle=1 / \sqrt{2}$).
Le but est de démontrer que $\mu_0(\lambda) \mu_{+}(\lambda)=0$ pour tout $\lambda$. On va le prouver par l’absurde en supposant qu’il y a une probabilité $q>0$ telle que les deux états quantiques résultent d’un $\lambda$ dans la région $\Delta$ de recouvrement.
Considérons maintenant deux systèmes dont les états physique ne sont pas corrélés. On peut les obtenir par exemple en opérant deux copies d’un dispositif de préparation indépendamment. Chaque système peut être préparé tel que son état quantique soit $|0\rangle$ ou $|+\rangle$.
Les états physiques $\lambda_1$ et $\lambda_2$ ont alors la probabilité $q^2>0$ d’être tous les deux dans la région de chevauchement $\Delta$.
Cela signifie qu’il y a une probabilité non nulle que l’état physique des deux systèmes soit compatible avec n’importe lequel des quatre états quantiques possibles $|0\rangle \otimes|0\rangle$, $|0\rangle \otimes|+\rangle$, $|+\rangle \otimes|0\rangle$ et $|+\rangle \otimes|+\rangle$.

Les deux systèmes sont ramenés ensemble et mesurés dans une base orthogonale particulière : $\left|\phi_1\right\rangle=\frac{1}{\sqrt{2}}[|0\rangle|1\rangle+|1\rangle|0\rangle]$, $\left|\phi_2\right\rangle=\frac{1}{\sqrt{2}}[|0\rangle|-\rangle+|1\rangle|+\rangle]$, $\left|\phi_3\right\rangle=\frac{1}{\sqrt{2}}[|+\rangle|1\rangle+|-\rangle|0\rangle]$ et $\left|\phi_4\right\rangle=\frac{1}{\sqrt{2}}[|+\rangle|-\rangle+|-\rangle|+\rangle]$.
Cette base a été choisie pour avoir $\left\langle\phi_1 \mid 00\right\rangle=0$, $\left\langle\phi_2 \mid 0+\right\rangle=0$, $\left\langle\phi_3 \mid+0\right\rangle=0$ et $\left\langle\phi_4 \mid++\right\rangle=0$.
Quel que soit le résultat de la mesure ($|\phi_1\rangle$, $|\phi_2 \rangle$, $|\phi_3 \rangle$ ou $|\phi_4 \rangle$), il élimine forcément l’une des possibilités ($|00\rangle$, $|0+\rangle$, $|+0\rangle$ ou $|++\rangle$). Cela entraîne que la probabilité de recouvrement des quatre états physiques est nulle. Contradiction !
Il y a $q^2$ chance que l’appareil de mesure ne sache pas laquelle des quatre méthode de préparation a été utilisée, et lorsque ça arrive, il prend le risque de produire un résultat qui n’est sensé jamais arriver.
Les hypothèses du théorème sont :
- il existe une réalité fondamentale $\lambda$,
- des $\lambda$ préparés séparément sont statistiquement indépendants,
- les prédictions statistiques de la mécanique quantique sont correctes,
- la réalité de l’état quantique (ψ-ontique) est définie comme le non recouvrement des distributions de probabilité de $\lambda$.
Selon ces hypothèses, $|\psi\rangle$ est réel ! Quelle que soit la propriété physique fondamentale $\lambda$, pour un $\lambda$ donné, $|\psi\rangle$ peut être déterminé de manière unique.
Pour certains, comme Antony Valentini, il s’agit du résultat le plus important concernant les fondations de la mécanique quantique depuis les inégalités de Bell.
Parmi les puristes ($\lambda\equiv|\psi\rangle$), des extra puristes ont décidé d’avaler la pilule des dimensions élevées pour regagner la localité et la séparabilité des états. En admettant que notre espace à trois dimensions n’est que l’ombre d’un espace multidimensionnelle dans lequel évolue la fonction d’onde, on évacue en effet toutes les galères (extra dimensions mises à part), du moins jusqu’à la mesure…
Cette petite page explique l’attrait de ce compromis.