Théorie-jouet de Spekkens
Spekkens, Robert W. (March 19, 2007). “Evidence for the epistemic view of quantum states: A toy theory”. Physical Review A. 75 (3): 032110 🌐
Hausmann, L., Nurgalieva, N. & del Rio, L. « A consolidating review of Spekkens’ toy theory », Working Paper, Institute for Theoretical Physics, ETH Zurich (7 mai 2021) 🌐
Knee, G. C. « Isolation of the Conceptual Ingredients of Quantum Theory by Toy Theory Comparison », mémoire de Master of Science, Imperial College London, soutenu le 20 septembre 2010 🌐
Aaronson, S. “Lecture 28, Tues May 2: Stabilizer Formalism”, Introduction to Quantum Information Science (cours de Scott Aaronson), 2 mai 2017 🌐
Spekkens propose en 2007 un modèle jouet qui reproduit qualitativement la physique d’un qubit à partir d’une théorie classique à laquelle on ajoute un principe limitant la connaissance qu’on peut obtenir sur n’importe quel système. La théorie permet d’éclairer certains phénomènes quantiques sous un autre jour, ce qui pour l’auteur devrait nous inciter à adopter une vision épistémique de l’état quantique. Dans cette vision, l’état quantique devient porteur d’une information incomplète sur une réalité sous-jacente, cachée. Étant donnée que la théorie de Spekkens est locale et que les inégalités de Bell impliquent qu’elle ne peut reproduire toute la mécanique quantique, d’où sa catégorisation en théorie-jouet.
Le système élémentaire
Le plus petit objet de la théorie de Spekkens est appelé système élémentaire. C’est l’objet ontique, l’objet réel de la théorie. Il peut se trouver dans l’un des quatre états ontiques possibles. On peut penser par exemple à un dé tétraédrique dont chaque face modélise un état possible.
On représente un système élémentaire par une rangée de quatre cases (une par état ontique).
Notre « opinion » sur le système, appelée état épistémique, est représentée par une disjonction (ou logique) d’états ontiques. Par exemple $a \lor b$ signifie : « le système est soit dans l’état ontique a, soit dans l’état b ».
Différents degrés de connaissance :
- ignorance totale :
$$1\lor2\lor3\lor4$$
- connaissance partielle :
$$1\lor2$$
- connaissance totale :
$$1$$
Exemple : la base ontique de $1 \lor 2 \lor 3 \lor 4$ est $\{1, 2, 3, 4\}$.
Pour un système élémentaire, si la base ontique d’un état épistémique contient $n$ états, alors la distribution de probabilité est uniforme sur ces $n$ états. Chaque case colorée porte la probabilité $1/n$.
Conséquences :
Dans l’état d’ignorance maximale ($1 \lor 2 \lor 3 \lor 4$), chaque case vaut $1/4$.
Dans l’état de connaissance partielle ($1\lor2$), chaque case vaut $1/2$.
Et dans l’état de connaissance parfaite ($1$), la case unique vaut $1$.
Lorsqu’on connaît tout, l’état épistémique coïncide avec l’état ontique, de même qu’une distribution de Dirac traduit la certitude parfaite sur une variable classique.
Le principe d’équilibre de la connaissance
Jusqu’ici, seuls des phénomènes classiques peuvent être reproduits par ce système. Pour obtenir des effets « quantiques » (comme la non‑commutation), il faut ajouter une contrainte informationnelle qui limite ce que l’on peut savoir sur l’état ontique. C’est précisément ce que fait le principe d’équilibre de la connaissance.
Schématiquement, le principe énonce qu’on ignore au moins autant qu’on connaît.
Quelques définitions pour préciser les choses :
ensemble minimal de questions oui/non suffisantes pour identifier sans ambiguïté l’état ontique d'un système donné.
Pour un système élémentaire dans les états ontiques 1, 2, 3 ou 4, un méthode inefficace pour déterminer l’état serait : $$\left\{ \begin{array}{l} \text{ ‘Est-ce 1 ?’},\\ \text{ ‘Est-ce 2 ?’},\\ \text{ ‘Est-ce 3 ?’},\\ \text{ ‘Est-ce 4 ?’} \end{array}\right\} $$
Alors que l’ensemble canonique parviendrait au même résultat avec seulement deux questions : $$\left\{ \begin{array}{l} \text{ ‘Est-ce 1 ou 2 ?’},\\ \text{ ‘Est-ce 2 ou 3 ?’} \end{array}\right\} $$
Chaque question coupe l’espace des possibles en deux. Pour un système élémentaire à 4 états, 2 questions suffisent donc (pas forcément ces deux là).
On peut maintenant définir plus proprement le principe d’équilibre des connaissances :
Une conséquence immédiate est que la connaissance maximale est incomplète.
Pour le système élémentaire : $K=I=1$. Une seule question peut être résolue, l’autre reste sans réponse. Cela revient à ne pouvoir écarter que deux états ontiques au maximum et donc en laisser deux possibles.
Il y a $\binom{4}{2}=6$ états possibles différents de connaissance maximale qu’on appellera bits-jouets (“bit” car il ne faut qu’un bit classique pour répondre à la question restée sans réponse dans l’ensemble canonique pour un système élémentaire) :
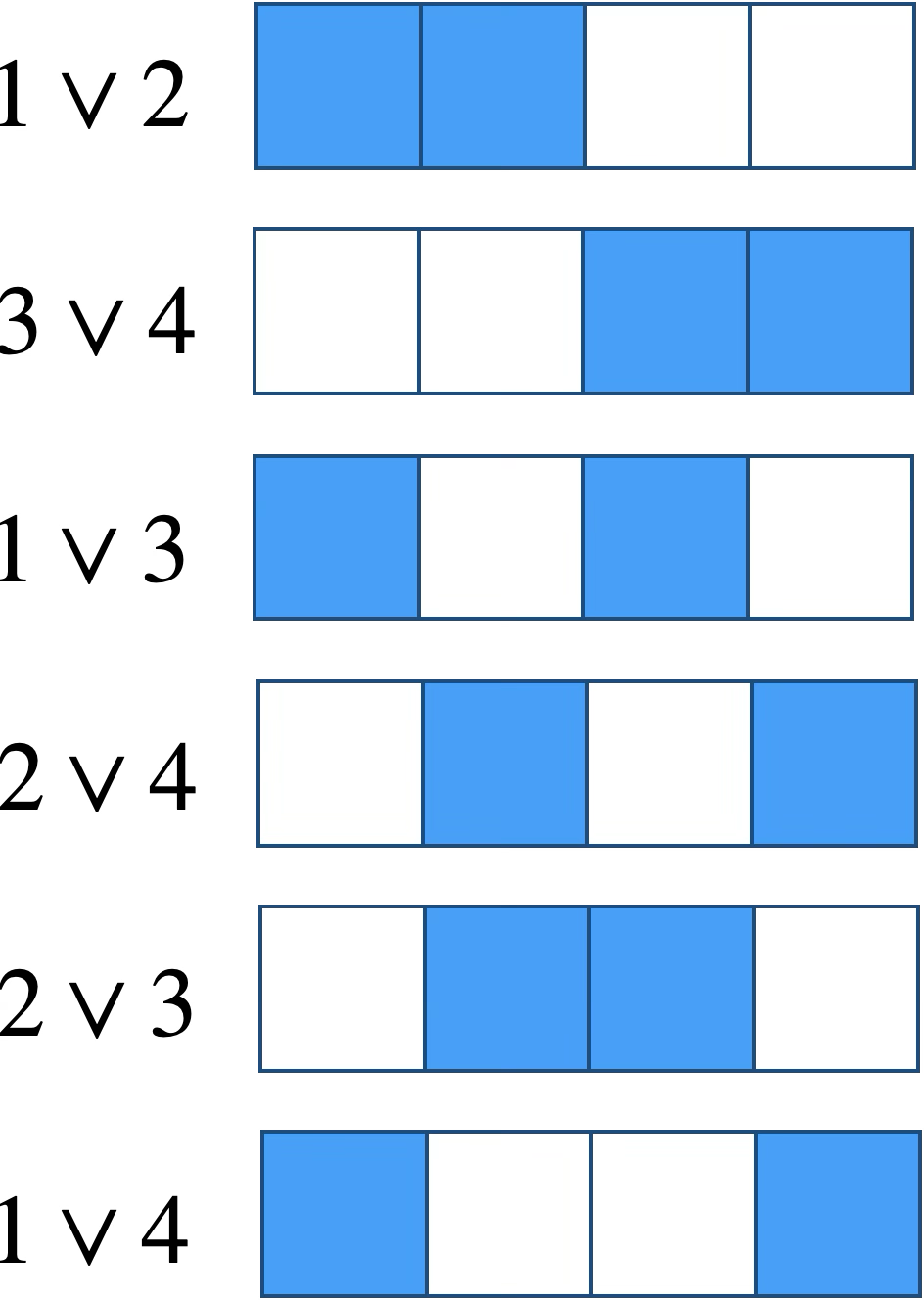
En ajoutant l’état d’ignorance maximale, on complète l’ensemble des sept états épistémiques autorisés pour un seul système élémentaire.
Et pourquoi ne pas ajouter les états épistémiques à 3 états ontiques type $(1\lor 2\lor 3)$ ?
Ce déficit de connaissance, imposé a priori, suffit à reproduire plusieurs effets clés de la mécanique quantique sans quitter un cadre fondamentalement classique.
Analogue d’un qubit état pur
On peut établir une correspondance bi‑univoque entre les sept états permis d’un bit‑jouet (épistémiques) et sept états particulièrement importants en information quantique : les six états propres $±1$ des trois matrices de Pauli $X$, $Y$, $Z$ et l’état maximalement mixte. Le « dictionnaire » est :
$$ \begin{array}{rcl} 1\lor2 &\longleftrightarrow& \lvert0\rangle \\ 3\lor4 &\longleftrightarrow& \lvert1\rangle \\ 1\lor3 &\longleftrightarrow& \lvert+\rangle \\ 2\lor4 &\longleftrightarrow& \lvert-\rangle \\ 2\lor3 &\longleftrightarrow& \lvert{+\mathrm i}\rangle \\ 1\lor4 &\longleftrightarrow& \lvert{-\mathrm i}\rangle \\ 1\lor2\lor3\lor4 &\longleftrightarrow& \tfrac{\mathbb I}{2} \end{array} $$
Représentations géométriques :
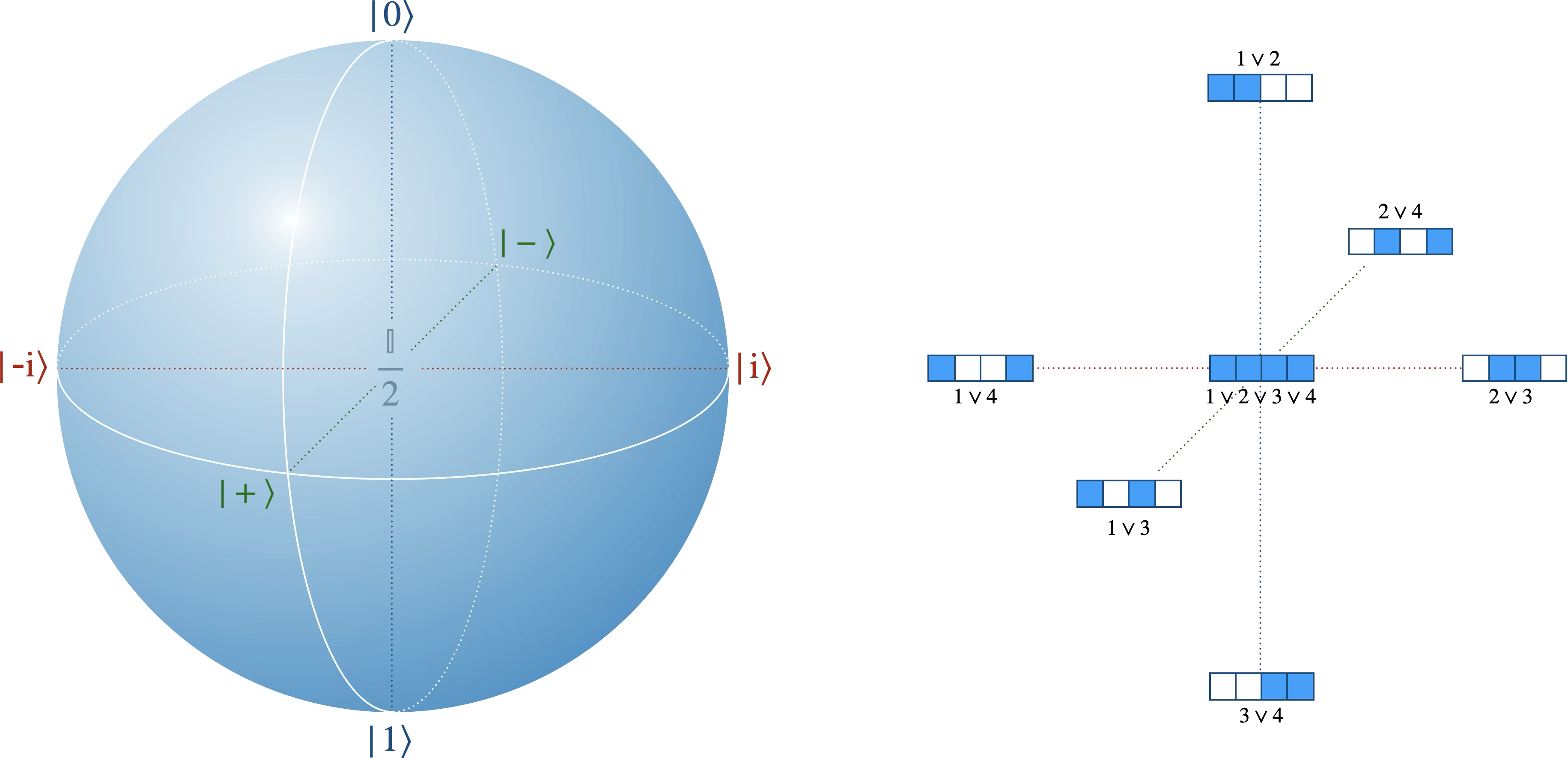
Deux états épistémiques sont disjoints si leurs bases ontiques n’ont aucun élément commun.
Les couples analogues aux paires orthogonales ($\lvert0\rangle$, $\lvert1\rangle$), ($\lvert+\rangle$, $\lvert-\rangle$), ($\lvert{+\mathrm i}\rangle$, $\lvert{-\mathrm i}\rangle$) deviennent ainsi trois paires de bits‑jouets diamétralement opposées, leur intersection vide se lisant d’un coup d’œil (aucune case colorées en commun).
La fidélité $\mathcal{F}[\bar{p},\bar{q}]$ entre deux états $a\lor b\lor c\lor d$ et $e\lor f\lor g\lor h$, où $p_k$ est un vecteur de probabilités uniformes pour $a$, $b$, $c$ et $d$ de somme unité, et $q_k$ est un vecteur de probabilités uniformes pour $e$, $f$, $g$ et $h$ de somme unité est définie par : $$\mathcal{F}[\bar{p},\bar{q}] \;=\; \sum_{k}\sqrt{p_k}\sqrt{q_k}$$
La fidélité est une mesure de la non disjonction. La disjonction et l’égalité sont deux cas particuliers de fidélités respectives $\mathcal{F}=0$ et $\mathcal{F}=1$.
Exemple pour les états épistémiques $1\lor 3$ et $1\lor 2$ :
Chaque état autorise exactement deux états ontiques et, par le principe d’uniformité, leur assigne la probabilité $1/2$.
Les valeurs de $p_k$ et $q_k$ sont donc :
| État ontique | $p_k$ pour $1\lor 3$ | $q_k$ pour $1\lor 2$ |
|---|---|---|
| $1$ | $1/2$ | $1/2$ |
| $2$ | $0$ | $1/2$ |
| $3$ | $1/2$ | $0$ |
| $4$ | $0$ | $0$ |
Calcul de la fidélité :
$$ \begin{aligned} \mathcal{F}[\bar{p},\bar{q}] &= \sum_{k=1}^{4}\sqrt{p_k}\,\sqrt{q_k}\\ &=\sqrt{\tfrac12}\sqrt{\tfrac12} \;+\; \sqrt{0}\sqrt{\tfrac12} \;+\; \sqrt{\tfrac12}\sqrt{0} \;+\; \sqrt{0}\sqrt{0} \\ &= \tfrac12 \;+\; 0 \;+\; 0 \;+\; 0 \\ &= \tfrac12 \end{aligned} $$
Et on obtient bien la même valeur de fidélité quantique entre les états qubits correspondants, $1\lor3 \;\longleftrightarrow\; |+\rangle$, $1\lor2 \;\longleftrightarrow\; |0\rangle$ : $|\langle+|0\rangle|^{2} = 1/2$.
La combinaison convexe de deux états épistémiques disjoints est l’union de leurs bases ontiques si cette union forme un état épistémique valide. Sinon, et pour les états non-disjonoints, la combinaison convexe est non définie.
La superposition cohérente de deux états épistémiques disjoints $(a\lor b)$ et $(c\lor d)$ avec $a,b≠c,d$, et $a<b,c<d$ est définie par :
$$ \begin{aligned} (a\lor b)\; +_1 \; (c\lor d) &= a\lor c,\\ (a\lor b)\; +_2 \; (c\lor d) &= b\lor d,\\ (a\lor b)\; +_3 \; (c\lor d) &= b\lor c,\\ (a\lor b)\; +_4 \; (c\lor d) &= a\lor d \end{aligned} $$
Les opérations binaires cohérentes associent des bits-jouets purs à d’autres bits-jouets purs (générant un analogue de la superposition cohérente de la mécanique quantique). Dans la représentation graphique, on associe à deux états diamétralement opposés (donc disjoints) un des quatre autres états.
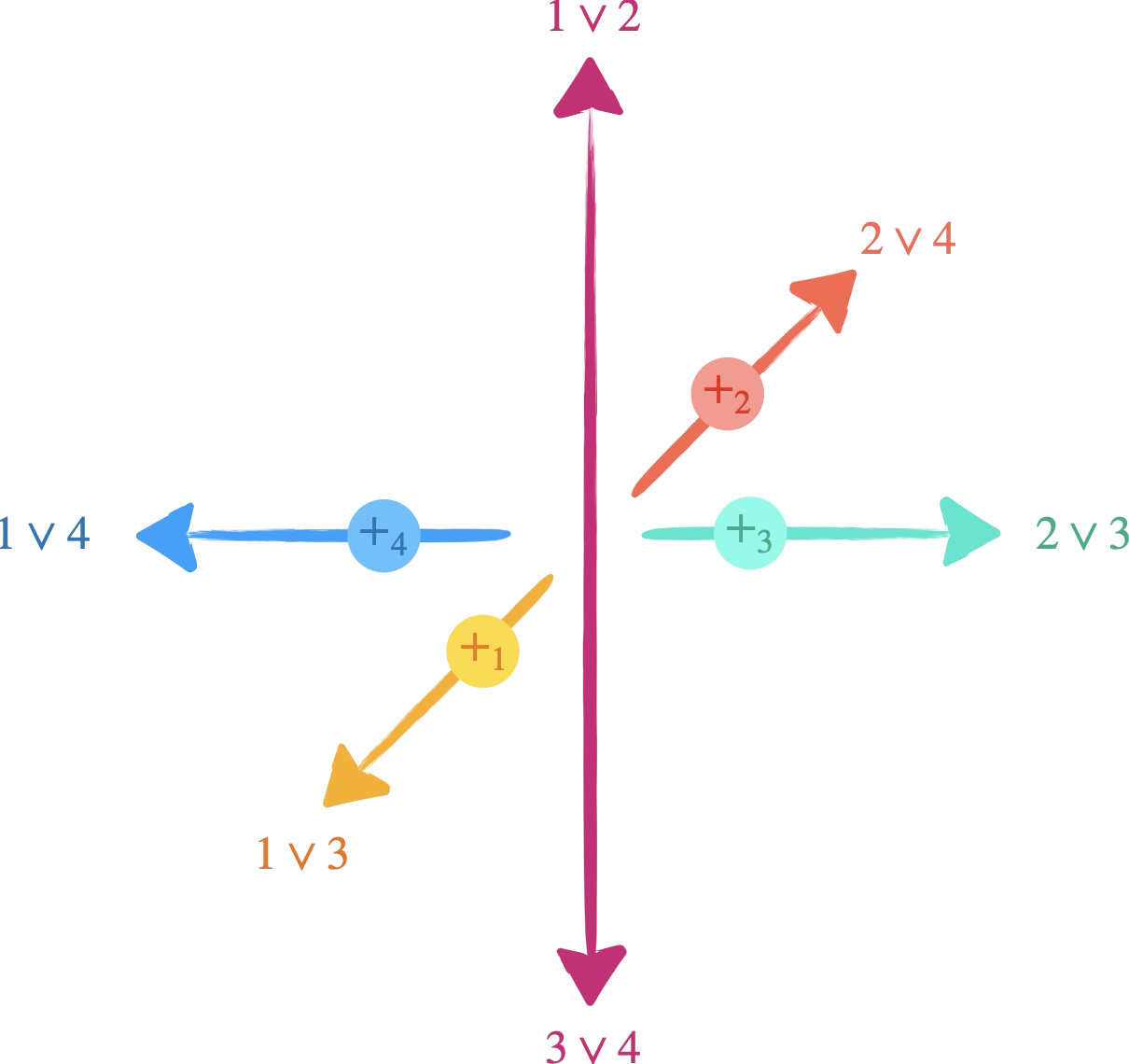
Les quatre opérations binaires cohérentes $+_1$, $+_2$, $+_3$, $+_4$ sont analogues aux superpositions de poids égaux de deux états purs de mécanique quantique avec une phase relative $\theta$ valant respectivement $0$, $\pi$, $\pi/2$, $3\pi/2$.
Exemple : en théorie jouet, $(1\lor 2)+_4(3\lor 4)=(1\lor 4)$, et en mécanique quantique, $\tfrac1{\sqrt{2}} (|0\rangle + \mathrm{e}^{\mathrm{i}\frac{3\pi}{2}} |1\rangle)=\tfrac1{\sqrt{2}} (|0\rangle -\mathrm{i} |1\rangle)=|-\mathrm{i}\rangle$.
Transformations
Dans la théorie-jouet, toute transformation valable doit conserver la fidélité entre états épistémiques.
C’est l’analogue exact de la conservation du produit scalaire par les transformations unitaires en mécanique quantique. Autrement dit, si deux états ont une fidélité $\mathcal{F}$ avant l’opération, ils auront la même fidélité après.
Les transformations permises sont donc seulement les permutations des quatre états ontiques. En effet, si une transformation envoyait plusieurs états ontiques sur un seul, elle pourrait faire passer un état épistémique légal (respectant le principe d’équilibre des connaissances) vers un état illégal qui le viole.
Exemple de la permutation $(123)(4)$ (permutation cyclique des états ontiques 1, 2 et 3 et absence de permutation pour l’état 4).
De $1\lor 2$, on obtient $2 \lor 3$. Et de $3\lor 4$, on obtient $1\lor 4$. La fidélité entre états initiaux (nulle ici) est bien conservée entre les états finaux.

Et cela reste vrai pour les 24 permutations des états ontiques éléments du groupe $S_4$.
Mesure
Dans la théorie-jouet comme en mécanique quantique, une mesure se doit de fournir un résultat mais aussi un état post-mesure.
En quantique, l’état post-mesure est le vecteur propre de l’observable associé à la valeur propre mesurée.
En théorie-jouet, l’état post-mesure doit continuer à obéir au principe d’équilibre de la connaissance. Autrement dit, la mise à jour doit éliminer tous les états ontiques incompatibles avec l’issue observée mais sans jamais laisser moins de deux états ontiques possibles pour un bit-jouet.
Le système élémentaire possédant 4 états ontiques, une mesure ne peut donc que les scinder en deux paquets de deux, ce qui donne $\binom{4}{2}=6$ partitions possibles. Mais certaines de ces partitions ne sont que des réétiquetages équivalents comme $\{a,b\}\,|\,\{c,d\}$ et $\{c,d\}\,|\,\{a,b\}$. Il ne reste finalement que trois directions de mesure, analogues des trois axes $X$, $Y$, $Z$ de mesure d’un qubit.
On note la mesure permettant de distinguer $a\lor b$ de $c\lor d$ avec les chiffres romains $\color{#1DB100}\text{I}$ et $\color{#D41876}\text{II}$ :
$$ \begin{array}{|c|c|c|c|} \hline \color{#1DB100}\text{I} & \color{#1DB100}\text{I} &\color{#D41876} \text{II} &\color{#D41876} \text{II}\\ \hline \end{array} = \{1\lor 2,3\lor 4\} \leftrightarrow \text{mesure sur l’axe }Z $$
$$ \begin{array}{|c|c|c|c|} \hline \color{#1DB100}\text{I} &\color{#D41876} \text{II} & \color{#1DB100}\text{I} &\color{#D41876} \text{II}\\ \hline \end{array} = \{1\lor 3,2\lor 4\} \leftrightarrow \text{mesure sur l’axe }X $$
$$ \begin{array}{|c|c|c|c|} \hline \color{#1DB100}\text{I} &\color{#D41876} \text{II} &\color{#D41876} \text{II} & \color{#1DB100}\text{I}\\ \hline \end{array} = \{1\lor 4,2\lor 3\} \leftrightarrow \text{mesure sur l’axe }Y $$
Deux états épistémiques disjoints (tout comme deux états quantiques orthogonaux) sont parfaitement distinguables par un choix appropriés de la direction de mesure. La mesure $\begin{array}{|c|c|c|c|} \hline \color{#1DB100} \text{I} &\color{#D41876} \text{II} &\color{#1DB100} \text{I} & \color{#D41876}\text{II}\\ \hline \end{array}$ permet par exemple de séparer avec certitude $1\lor 3$ et $2\lor 4$.
Donc si on utilise $\begin{array}{|c|c|c|c|} \hline \color{#1DB100} \text{I} &\color{#D41876} \text{II} &\color{#1DB100} \text{I} & \color{#D41876}\text{II}\\ \hline \end{array}$ sur $2\lor 4$, l’état post-mesure sera toujours $2\lor 4$.
Certaines mesures peuvent laisser une ambigüité comme $\begin{array}{|c|c|c|c|} \hline \color{#1DB100}\text{I} &\color{#D41876} \text{II} &\color{#1DB100} \text{I} &\color{#D41876} \text{II}\\ \hline \end{array}$ sur $1\lor 2$. Puisque l’état ontique est soit en $1$, soit en $2$, les deux résultats de mesures $1\lor 3$ et $2\lor 4$ sont possibles et obtenus avec la même probabilité.
Il est important de noter que l’incertitude ici n’est pas fondamentale mais la conséquence du manque de connaissance initiale sur la position de l’état ontique.
Mais un problème se pose… Imaginons que la mesure $\begin{array}{|c|c|c|c|} \hline \color{#1DB100}\text{I} &\color{#D41876} \text{II} &\color{#1DB100} \text{I} &\color{#D41876} \text{II}\\ \hline \end{array}$ opérée sur l’état $1\lor 2$ donne $1\lor 3$. Cela nous indique avec certitude où était l’état ontique (en $1$) ! Jusque-là, rien ne viole réellement le principe d’équilibre de la connaissance puisqu’il nous interdit de connaître l’état ontique actuel et ne dit rien sur l’état ontique passé. Par contre, il impose de fait que l’état post-mesure ne puisse pas être simplement $1$. Il faut alors s’imaginer que la mesure ait perturbé le système en distribuant l’état ontique aléatoirement sur les deux états possibles mesurés $1$ ou $3$. Il y a donc un déplacement caché de l’état ontique post-mesure.
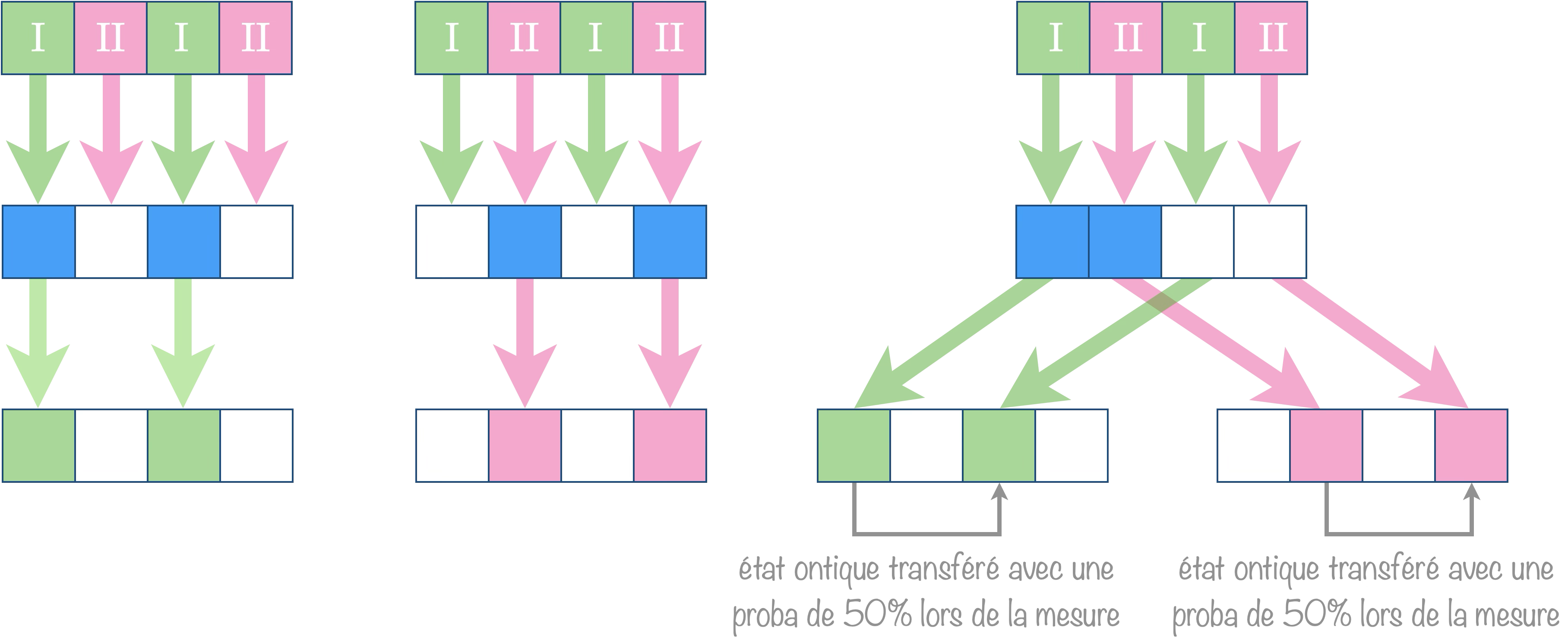
Lorsque les états mesurés ne contiennent qu’un seul état ontique, la mesure distribue uniformément l’état ontique sur les deux états mesurés.
Paires de systèmes élémentaires
Tout système se construit à partir de systèmes élémentaires.
Pour un assemblage de $n$ éléments :
- l’ensemble canonique comporte $2n$ questions ;
- il existe $2^{2n}$ états ontiques possibles (chaque question divisant par 2 l’ensemble des possibilités).
Considérons deux systèmes élémentaires simultanément : leurs états ontiques forment le produit cartésien des états individuels, exactement comme un produit tensoriel en mécanique quantique.
Il y a donc 16 couples possibles notés $(a\cdot b)$ où $a$ et $b$ sont les états ontiques du premier et deuxième système respectivement :
$$ \left\{ \begin{array}{llll} (4 \cdot 1), & (4 \cdot 2), & (4 \cdot 3), & (4 \cdot 4), \\ (3 \cdot 1), & (3 \cdot 2), & (3 \cdot 3), & (3 \cdot 4), \\ (2 \cdot 1), & (2 \cdot 2), & (2 \cdot 3), & (2 \cdot 4), \\ (1 \cdot 1), & (1 \cdot 2), & (1 \cdot 3), & (1 \cdot 4) \end{array} \right\} $$
On peut représenter ces 16 états ontiques sur une grille :
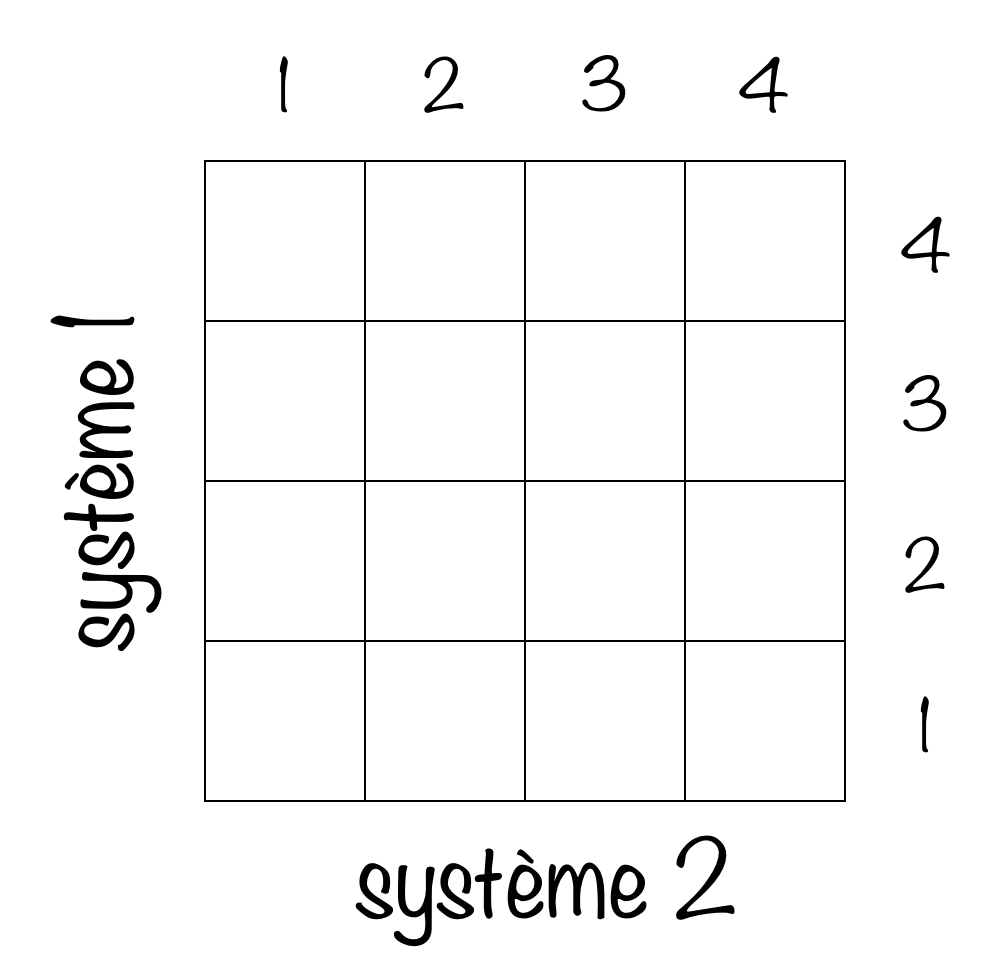
Exemple : l’état joint $(1\cdot 1)$ (système 1 dans l’état 1 et système 2 dans l’état 1).

Ce n’est pas un état épistémique valide pour deux raisons :
- si on regarde isolément un des systèmes en ignorant l'autre, on n'obtient qu'un seul état ontique et donc on peut répondre à plus de la moitié des questions pour l'ensemble canonique de ce sous-système.
- En appliquant le principe d'équilibre des connaissance au système composite entier, on est sensé ne pouvoir répondre qu'à $2$ des $2n=4$ questions. Or un état ontique unique fixe d'un coup les $4$ réponses.
Cet exemple nous montre que :
Dans un système bipartite de bits-jouets, au moins quatre cases doivent être colorées pour respecter le principe d’équilibre des connaissances.
Cela implique qu’il y ait $\binom{16}{4}=1820$ états épistémiques « de connaissance maximale » pour le système composite.
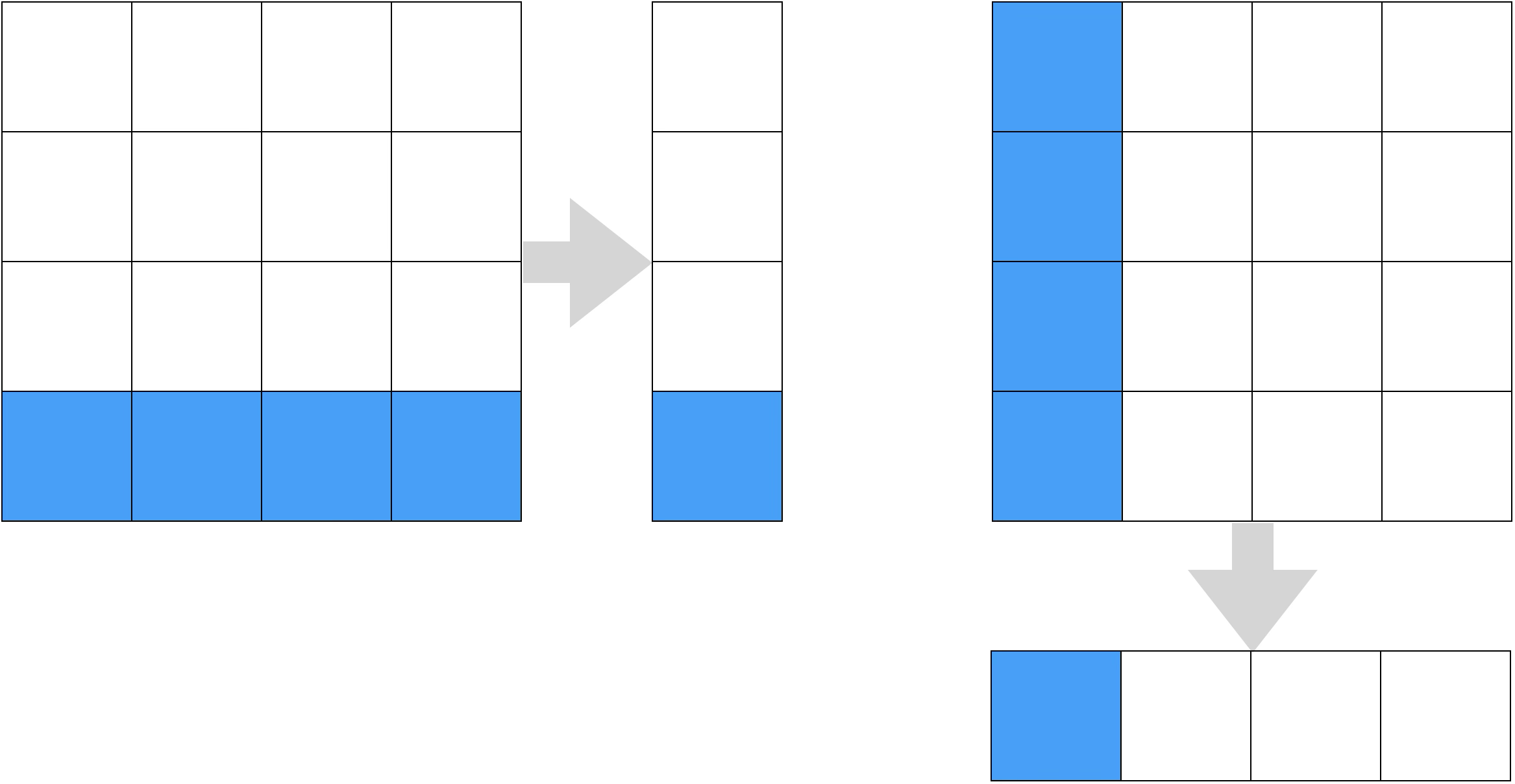
Lorsqu’on ignore l’information concernant un sous-système, on obtient une distribution marginale1 du système composite :
- ignorer le système 1 revient à projeter toutes les lignes sur une sous-ligne unique,
- ignorer le système 2 revient à projeter toutes les colonnes sur une sous-colonne unique.
Cette opération joue un rôle analogue à la trace partielle en mécanique quantique.
Le principe d’équilibre doit être respecté à la fois sur le système composite et sur ses marginales. Et une marginale admissible doit contenir plus de 2 états ontiques.
Cela permet de rejeter certains des $1820$ états à 4 cases colorées puisqu’ils violent le principe d’équilibre des connaissance sur l’un de leurs sous-systèmes.
Les deux exemples ci-dessous sont par exemple invalides ; dans l’exemple de gauche, le principe est violé pour le système 1 et dans l’exemple de droite, c’est pour le système 2.
D’autres états doivent être écartés car ils mèneraient, après certaines mesures, à un post-état qui ne respecterait pas le principe d’équilibre de la connaissance.
Mesures sur des états bipartites
On appelle état produit tout état bipartite dans lequel on possède la quantité maximale d’information autorisée sur chaque sous-système, en tenant compte du principe d’équilibre de la connaissance appliqué :
- au système composite,
- et à chacun des deux sous-systèmes pris isolément
Si le système 1 a pour marginale $a\lor b$ et le système 2 la marginale $c\lor d$, l’état produit s’écrit :
$$(a\lor b)\,\cdot\,(c\lor d)\;=\; (a\cdot c)\;\lor\;(b\cdot c)\;\lor\;(a\cdot d)\;\lor\;(b\cdot d)$$
c’est-à-dire qu’on distribue la disjonction sur la conjonction exactement comme on développe $(x+a)(y+b)=xy+ay+xb+ab$ en algèbre élémentaire.
Règle de mise à jour post-mesure :
- la distribution marginale du sous-système est projetée sur la zone du résultat ($\color{#1DB100}\text{I}$ ou $\color{#D41876}\text{II}$),
- l'autre marginale devient l'intersection entre la marginale avant mesure et la zone compatible avec le résultat obtenu.
L’état global est donné par le produit des deux marginales mises à jour.
Premier exemple :
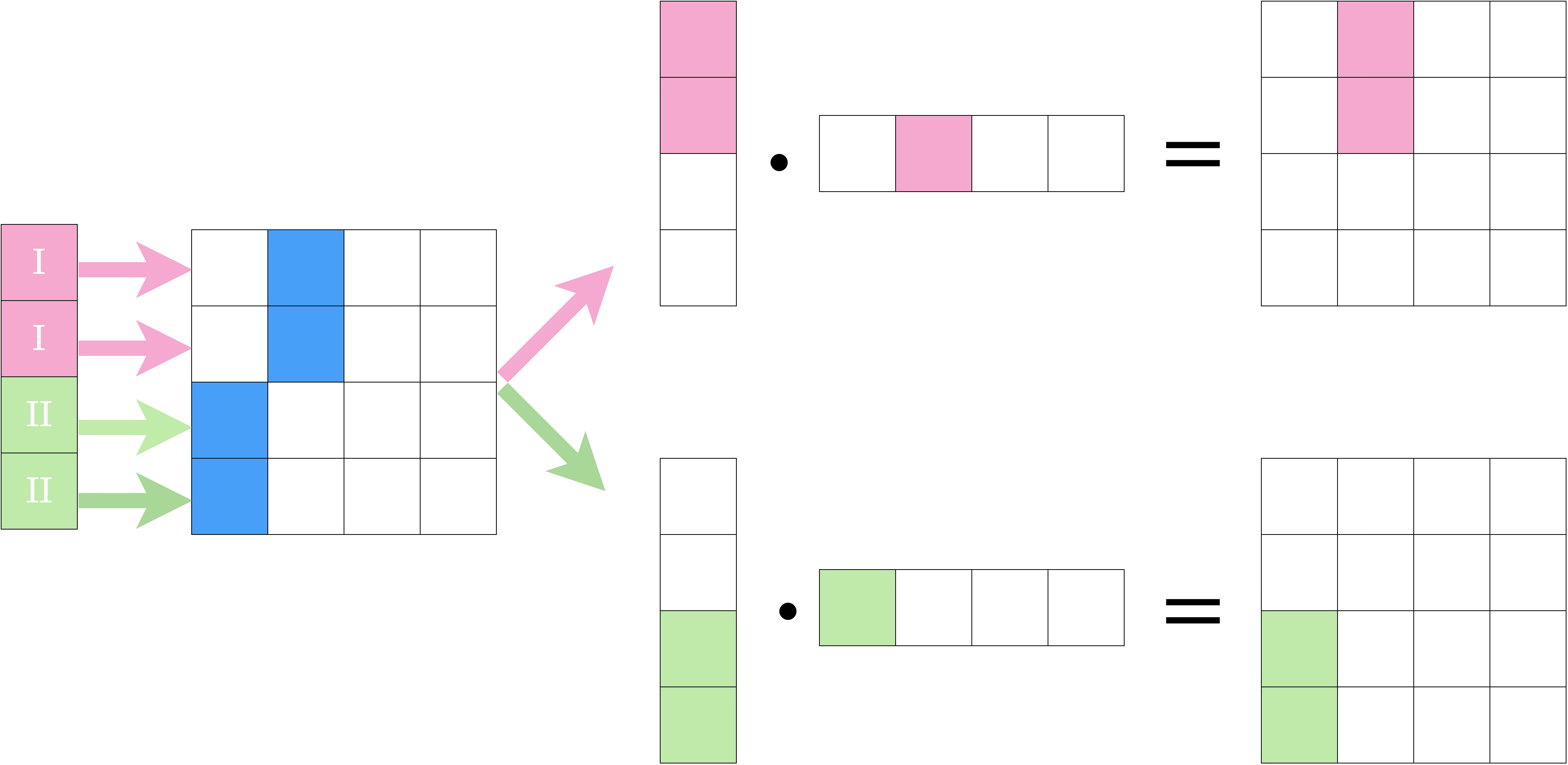
Les deux états obtenus sont invalides ce qui permet de retirer l’état de départ des états bipartites possibles.
Deuxième exemple :
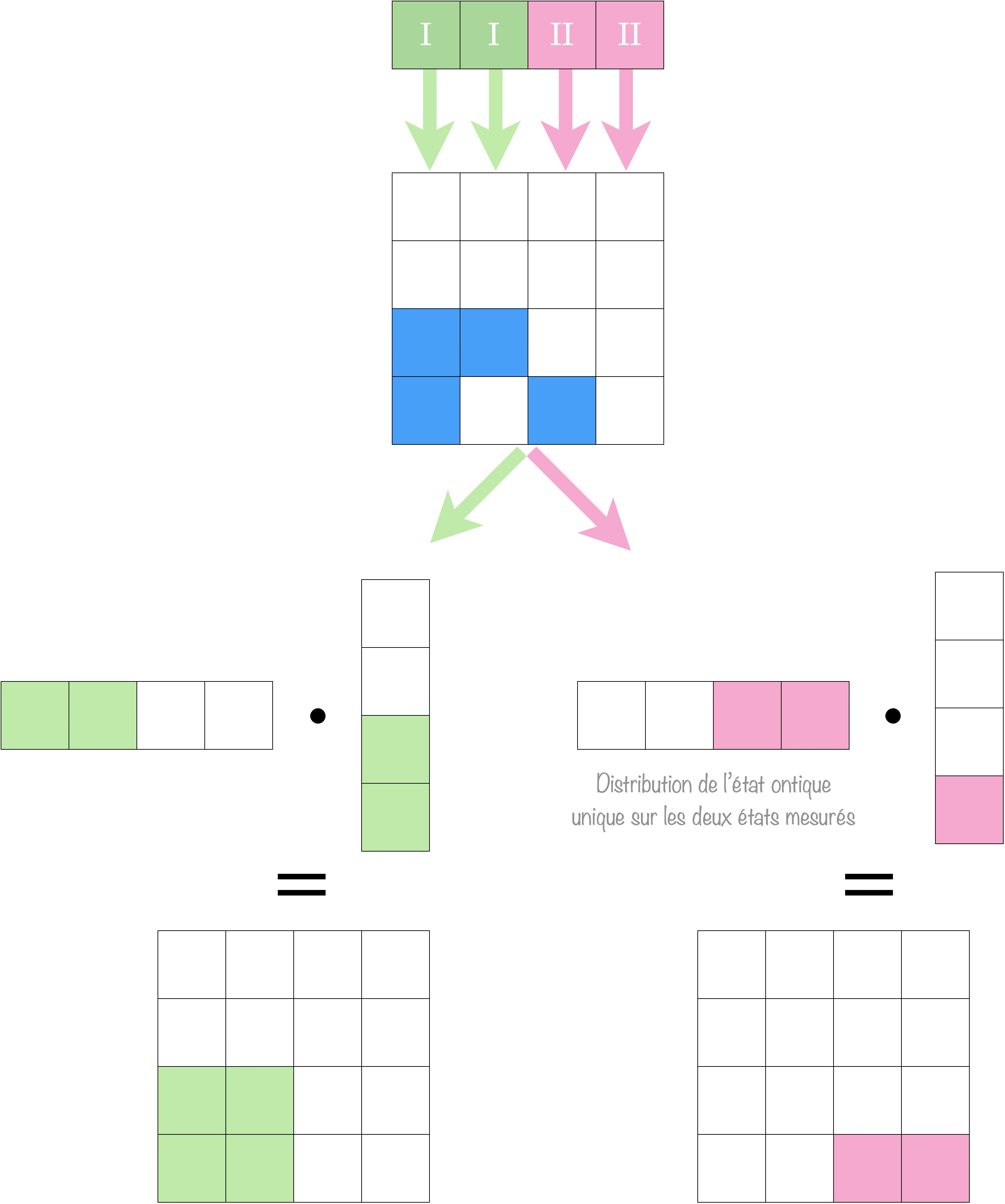
Ici, seule l’issue $\color{#D41876}\text{II}$ est invalide mais cela suffit pour écarter là encore l’état de départ.
L’interdiction de pouvoir localiser simultanément les deux états ontiques imposant qu’au final au moins 4 possibilités demeurent impose finalement un tri sévère.
États corrélés
Un état corrélé est un état biparti dans lequel on possède une connaissance complète de la relation entre les deux sous-systèmes, mais aucune information sur l’état ontique de chacun pris séparément : leurs marginales sont donc l’ignorance totale (quatre possibilités chacune).
L’exemple canonique est $(1·1)\;\lor\;(2·2)\;\lor\;(3·3)\;\lor\;(4·4)$, ainsi que tous les états obtenus par permutation des lignes ou des colonnes.
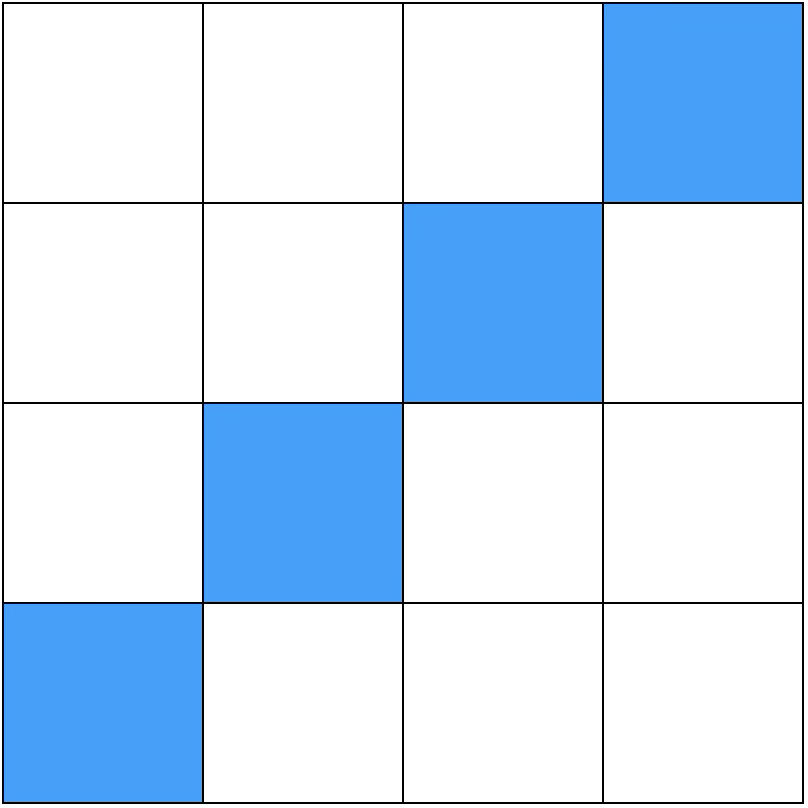
Cet état n’est pas factorisable puisqu’il lui manque les « termes croisés » $(1·2),\,(2·1),\dots$, exactement comme un état intriqué en mécanique quantique ne peut s’écrire sous forme de produit de deux fonctions d’onde locales.
Que peut-on dire de l’état suivant ?

Il respecte le principe d’équilibre de la connaissance (nombre d’états quantiques $>4$ sur le système composite et $>2$ sur chaque marginale) et comme on a 8 états ontiques plutôt que les 4 attendus pour un bit-jouet pur, on est en présence d’un état mixte.
Les marginales sont toutes deux $1\lor 2\lor 3\lor 4$, ce qui correspond à une ignorance totale. Leur produit cartésien serait la grille complète de 16 cases, pas seulement 8. Il ne s’agit donc pas d’un état produit mais d’un état corrélé.
C’est une corrélation “par blocs” : connaître un des deux états-jouets détermine le demi-espace de l’autre mais pas une valeur unique. Et chaque bloc est un état produit de deux états purs ($(1\lor 2)\cdot(1\lor 2)$ pour le bloc du bas et $(3\lor 4)\cdot(3\lor 4)$ pour celui de haut).
On a donc au final une corrélation statistique plutôt qu’une corrélation pure, un mélange classique de deux états produits.
Cardinalité des états
Pour un composé de n systèmes élémentaires, il existe $4^{n}$ états ontiques possibles et $2n$ questions binaires dans un ensemble canonique.
Si l’on répond à la moitié de ces questions ($n$ réponses), on réduit l’incertitude à $2^{n}$ états ontiques. Tout état épistémique « de connaissance maximale » contient donc exactement $2^{n}$ cases colorées.
Le nombre total d’états qui satisfont ainsi le principe d’équilibre de la connaissance est $\bar{\Omega}_n=\binom{4^n}{2^n}$.
Pour deux bits-jouets ($4^{2}=16$ cases, $2^{2}=4$ cases à colorier), cela donne les 1820 possibles évoqués plus haut mais comme on l’a vu, beaucoup de ces états sont en réalité illégaux.
Au final, les seuls états bipartites de connaissance maximale autorisés (bits-jouets bipartites purs) sont :
- les états produits,
- les états corrélés.
Comptage détaillé :
- états produits : on choisit 2 lignes parmi 4 et 2 colonnes parmi 4 et on colore l'intersection ce qui représente $\binom{4}{2} \cdot\binom{4}{2}=36$ possibilités.
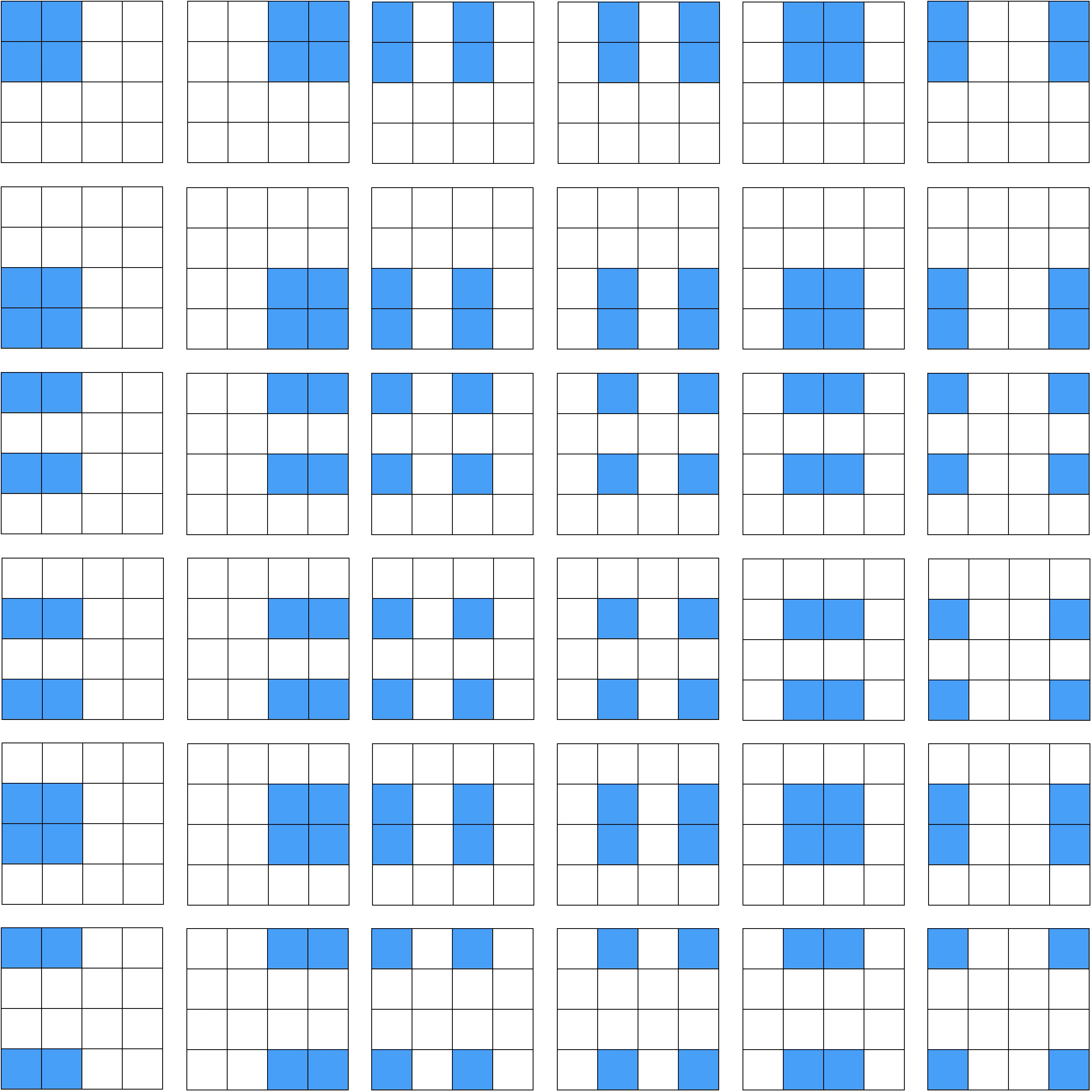
- états corrélés : on choisit une permutation complète des 4 indices ce qui représente $4!=24$ possibilités.

Cela donne en tout $60$ bits-jouets purs pour deux systèmes élémentaires.
Interdiction du clonage
Dans la théorie-jouet, « cloner » un état de connaissance incomplète signifie appliquer ce même état épistémique à un second système tout en le conservant pour le premier. Il ne s’agit pas de « dupliquer une part de la réalité » puisque les états épistémiques ne font pas partie de la réalité physique mais seulement de notre interprétation. Tout comme les états quantiques, les états-jouets sont également non-clonables.
Un cloneur idéal devrait réaliser la transformation
$$(a\lor b)\;\cdot\;(c\lor d)\;\longrightarrow\;(a\lor b)\;\cdot\;(a\lor b) \tag{a}$$
où ($a\lor b$) est le bit-jouet de données et ($c\lor d$) un état ancillaire arbitraire.
Pour être universel, le même dispositif devrait aussi accomplir
$$(e\lor f)\;\cdot\;(c\lor d)\;\longrightarrow\;(e\lor f)\;\cdot\;(e\lor f)\tag{b}$$
pour tout autre bit-jouet ($e\lor f$).
La fidélité entre $(a)$ et $(b)$ nous donne
$$ \mathcal{F}\!\bigl[(a\lor b),(e\lor f)\bigr]\; \longrightarrow\; \bigl[\mathcal{F}\!\bigl[(a\lor b),(e\lor f)\bigr]\bigr]^{2} $$
où on suppose $\mathcal{F}\!\bigl[(a\lor b)\cdot(c\lor d),(e\lor f)\cdot(c\lor d)\bigr] =\; \mathcal{F}\!\bigl[(a\lor b),(e\lor f)\bigr]\;\times\;\mathcal{F}\!\bigl[(c\lor d),(c\lor d)\bigr]$.
La relation obtenue n’a de solution que si :
- $\mathcal{F} = 1$ (les deux états sont identiques)
- $\mathcal{F} = 0$ (les deux états sont disjoints)
Comme les seules transformations autorisées dans la théorie-jouet sont celles qui préservent la fidélité, on conclut qu’un cloneur universel est impossible.
Formalisme stabilisateur
Une restriction discrète de la mécanique quantique permet de dresser un parallèle assez fort avec la théorie jouet : le formalisme stabilisateur. Il a été inventé pour décrire les codes correcteurs d’erreurs quantiques, mais il sert aujourd’hui aussi à la simulation efficace de certains circuits quantiques, à la cryptographie, à l’algorithmique et à l’informatique “à état magique”.
Deux points d’entrée complémentaire pour présenter ce formalisme :
- par les portes quantiques,
- par les matrices de Pauli.
3 portes quantiques
Les 3 portes élémentaires Hadamard ($H=\frac{1}{\sqrt{2}}\left[\begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array}\right]$), phase ($P=\frac{1}{\sqrt{2}}\left[\begin{array}{cc} 1 & 0 \\ 0 & \mathrm{i} \end{array}\right]$) et CNOT (retourne le qubit cible si et seulement si le qubit de contrôle est $|1\rangle$), sont appelées portes stabilisatrices.
Un circuit quantique composé entièrement de portes stabilisatrices est un circuit stabilisateur.
Un état stabilisateur est un état qu’un circuit stabilisateur peut générer à partir de l’état $|00\ldots 0\rangle$.
Voyons ce que l’on obtient à partir d’un seul qubit et des portes $H$ et $P$ :
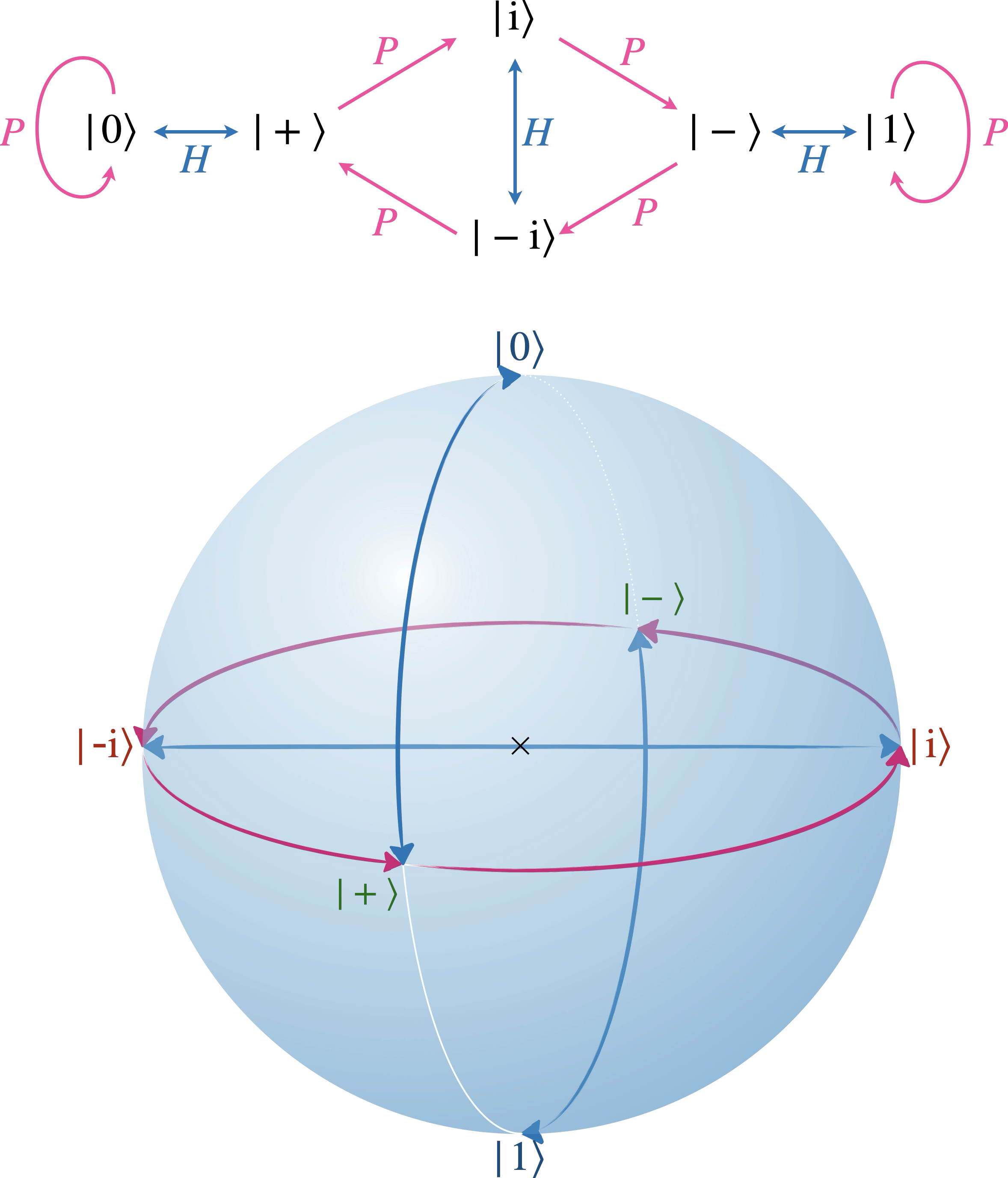
Ces 6 qubits qui, comme on l’a vu, ont leur contrepartie chez les jouets, sont les 1-qubits stabilisateurs.
À partir de deux qubits, la porte CNOT nous permet d’atteindre des états intriqués comme les états de Bell. Montrons par exemple comment fabriquer $\frac{|00\rangle+|11\rangle}{\sqrt{2}}$ en partant de $|00\rangle$ :
- on crée une superposition locale sur le premier qubit (qubit de contrôle) grâce à $H$ : $ (H \otimes I)|00\rangle=\frac{|0\rangle+|1\rangle}{\sqrt{2}} \otimes|0\rangle=\frac{|00\rangle+|10\rangle}{\sqrt{2}} $,
- puis on ajoute l'intrication grâce à CNOT (contrôle = qubit 0, cible = qubit 1) $\Rightarrow \frac{|00\rangle+|11\rangle}{\sqrt{2}}$.
Il y a 60 états atteignables à 2 qubits (autant que les bits-jouets à nouveau). Et pour chacun, une mesure dans la base $\{|0\rangle,|1\rangle\}$ donne soit $|0\rangle$, soit $|1\rangle$, soit $|0\rangle$ et $|1\rangle$ avec des probablités égales.
Matrices de Pauli
On dit qu’un opérateur unitaire $U$ stabilise un état pur $|\Psi\rangle$ si $U|\Psi\rangle=|\Psi\rangle$ ($|\Psi\rangle$ est donc un état propre de $U$ pour la valeur propre +1).
Attention, la phase est importante ici : si $U|\Psi\rangle=-|\Psi\rangle$, alors $U$ ne stabilise pas $|\Psi\rangle$.
Si $U$ et $V$ stabilisent tous deux $|\Psi\rangle$, alors $UV$ et $VU$ aussi, ainsi que $U^{-1}$ et $V^{-1}$. Et comme $I$ stabilise tout, l’ensemble des opérateurs unitaires qui stabilisent $|\Psi\rangle$ forment un groupe multiplicatif.
Vérifions maintenant que chacun des six états stabilisateurs à 1 qubit correspondent à une matrice de Pauli qui le stabilise :
- $I$ stabilise tout
- $-I$ ne stabilise rien
- $X$ stabilise $|+\rangle$
- $-X$ stabilise $|-\rangle$
- $Z$ stabilise $|0\rangle$
- $-Z$ stabilise $|1\rangle$
- $Y$ stabilise $|\mathrm{i}\rangle$
- $-Y$ stabilise $|-\mathrm{i}\rangle$
Les matrices de Pauli permettent d’opérer chaque type d’erreur de code (d’où leur omniprésence dans le monde des codes correcteurs) :
- pas d'erreur : $I|1\rangle = |1\rangle$
- retournement de bit : $X|1\rangle = |0\rangle$
- retournement de phase : $Z|1\rangle = -|1\rangle$
- les deux à la fois : $Y|1\rangle = -\mathrm{i}|0\rangle$
Pour un $n$-qubit $|\Psi\rangle$, on définit le groupe stabilisateur de $|\Psi\rangle$ comme le groupe de tous les produits tensoriels de matrices de Pauli qui stabilisent $|\Psi\rangle$.
Exemple : quel est le groupe stabilisateur de l’état de Bell $\frac{|00\rangle+|11\rangle}{\sqrt{2}}$ ?
$XX$ est dedans puisque $\frac{X|0\rangle \otimes X|0\rangle+X|1\rangle \otimes X|1\rangle}{\sqrt{2}}=\frac{|11\rangle+|00\rangle}{\sqrt{2}}=\frac{|00\rangle+|11\rangle}{\sqrt{2}}$.
De même pour $-YY$ et le résultat de la multiplication $XX\cdot-YY = -(\mathrm{i}Z)(\mathrm{i}Z) = ZZ$.
Le groupe au complet est alors $\{II,XX,-YY-ZZ\}$.
Les états stabilisateurs à $n$-qubits sont exactement les états à $n$-qubits qui ont un groups stabilisateur de taille $2^n$.
Les états stabilisateurs à 1 qubit sont ainsi les états ayant un groupe stabilisateur à 2 éléments, les états stabilisateurs à 2 qubits sont ceux avec un groupe à 4 éléments, etc.
On a ainsi caractériser les états stabilisateurs d’une manière complètement différente, sans mention de circuit stabilisateur. Cela nous a permis d’en savoir plus sur l’invariant que les circuits stabilisateurs préservent.
-
Petit cours sur les distribution conjointe et marginale en probabilité. ↩︎