Une ontologie à 3N dimensions
Ontologie de la fonction d’onde
Ney, A. « Three arguments for wave function realism », European Journal for Philosophy of Science, vol. 13, art. 50 (24 octobre 2023).
Donner une réalité à la fonction d’onde $\psi$, c’est accepter que notre espace 3D ne soit qu’une projection de l’espace à 3N dimensions dans lequel $\psi$ vit.
Pourquoi 3N dimensions ?
En mécanique quantique, la fonction d’onde est construite comme un champ sur un espace de $3N$ dimensions où $N$ est le nombre de particules.
Pourquoi s’embêter avec ces dimensions supplémentaires ?
À cause des intrications.
Supposons que l’on ait deux particules préparées dans un état singulet de spin $|\uparrow\downarrow\rangle-|\downarrow\uparrow\rangle$. Les particules sont ensuite envoyées dans des directions opposées vers deux Stern-Gerlach qui vont les dévier vers le haut ou vers le bas en fonction de la valeur de leur spin selon l’axe $z$.
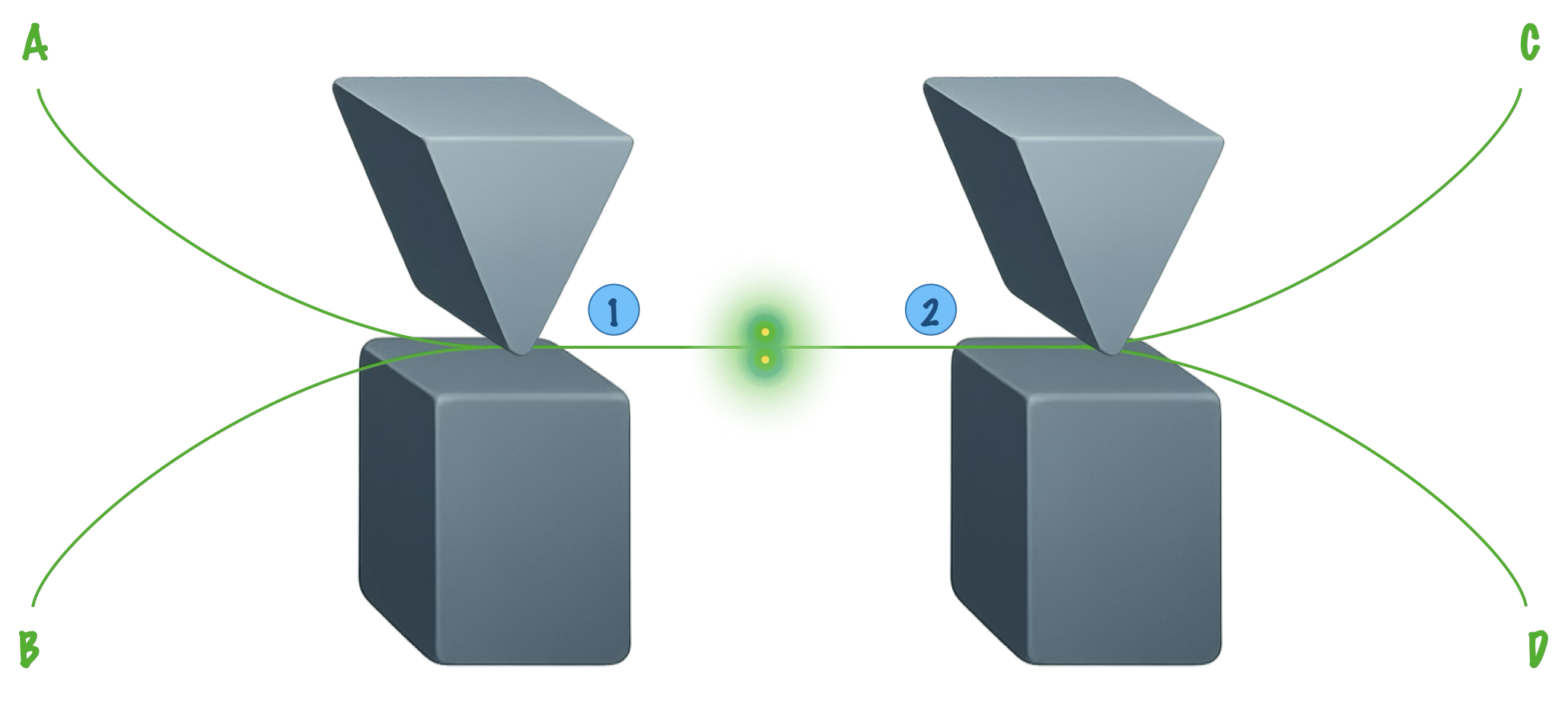
On appelle $\text{A}$, $\text{B}$, $\text{C}$ et $\text{D}$ les 4 localisations possibles après les déflections.
Comme les particules deviennent intriquées avec les appareils de mesure, elles se trouvent au final dans un état intriqué non pas seulement par rapport à leurs spins mais aussi par rapport à leurs positions :
À 3-D, on ne peut pas interpréter cet état quantique comme un seul champ si on veut qu’il attribue des propriétés intrinsèques et séparables à chaque particule. Il faut donc deux champs dont les composantes correspondront aux différentes positions.
Supposons maintenant que les deux particules ne soient pas dans un état intriqué mais dans un état produit $|\uparrow_x\rangle_1\otimes |\uparrow_x\rangle_2$. Après les Stern-Gerlach, on a :
On peut essayer à nouveau de décrire cet état par deux champs à 3-D.
Mais comment alors peut-on distinguer les deux états quantiques ? Les deux champs obtenus ont bien, chacun, la même densité sur $\text{A}$, $\text{B}$, $\text{C}$ et $\text{D}$ ; en 3-D on ne voit donc aucune différence.
Par contre, si on interprète ces états quantiques non plus comme deux champs à 3-D mais un champ à 6-D, on capture la corrélation entre les états de $\psi$ et donc la distinction avec $\psi^\prime$.
Il suffit pour cela de considérer 4 points dans l’espace à 6-D désignés de manière transparente par $\text{AC}$, $\text{AD}$, $\text{BC}$ et $\text{BD}$ (le point $\text{AC}$ dans l’espace 6-D des configurations correspond à la situation dans l’espace 3-D où la particule 1 est localisée en $\text{A}$ et la particule 2 est localisée en $\text{C}$).
Dans cet espace à 3N-D, $\psi$ décrit un champ avec seulement des composantes en $\text{AD}$ et $\text{BC}$. $\psi^\prime$, lui, décrit un champ avec des composantes aux 4 points $\text{AC}$, $\text{AD}$, $\text{BC}$, $\text{BD}$.
Le schéma bi-champ efface la corrélation “si et seulement si” entre la localisation de 1 et celle de 2.
Séparabilité et localité
Vouloir décrire la fonction d’onde dans un espace impose d’accepter la non séparabilité et/ou la non localité de la théorie.
-
Une métaphysique est séparable si les parties (R1 et R2) permettent de déduire le tout (R1 $\cup$ R2) .
-
La localité signifie que deux régions non causalement reliées ne peuvent pas s’influencer.
Une motivation pour une théorie séparable et locale est l’obtention d’une ontologie simple, propre, parcimonieuse (rasoir d’Ockham) :
les faits concernant une entité ne dépendent pas des faits concernant une autre, et un objet ne peut pas agir là où il n’est pas.
Dans l’ontologie de la fonction d’onde, la physique est bien séparable et locale (mais dans l’espace à 3N-D, pas dans l’espace 3-D). En effet :
- L’unique objet ontique est un champ $\psi$ sur l’espace des configurations $\mathbb R^{3N}$.
- L’équation de Schrödinger est une équation aux dérivées partielles locales dans cet espace : $\partial_t\psi(q,t)=\hat H(q)\psi(q,t)$.
- Un « point » $q=(\mathbf r_1,\mathbf r_2,\dots)$ est par construction une région élémentaire ; donner $\psi$ sur deux sous-régions disjointes $Q_1,Q_2\subset\mathbb R^{3N}$ suffit à fixer $\psi$ sur leur union.
Revenons à l’état singulet avec les deux stern-Gerlach.
-
La fonction d’onde sur les deux points $q_{\text{AD}}=\text{AD}$ et $q_\text{BC}=\text{BC}$ dans $\mathbb R^{6}$ s’écrit $\psi(q)=\tfrac1{\sqrt2}\bigl[\delta(q-q_\text{AD})-\delta(q-q_\text{BC})\bigr]$.
Restreindre $\psi$ à la petite boule $Q_\text{AD}$ autour de $q_{\text{AD}}$ et à $Q_\text{BC}$ autour de $q_\text{BC}$ suffit pour connaître tout $\psi$. Cela montre la séparabilité.
À 3D par contre, comme on l’a vu, connaître $|\phi_1|^2$ sur les points $\text{A}$ et $\text{B}$ et $|\phi_2|^2$ sur $\text{C}$ et $\text{D}$ ne détermine pas la corrélation « $\text{A} \leftrightarrow \text{D}, \text{B} \leftrightarrow \text{C} $ ». L’état intriqué et l’état produit restent indistinguables. La théorie n’est donc pas séparable si l’espace 3D est fondamental. -
L’évolution de $\psi$ en $Q_{\text{AD}}$ dépend seulement de $\psi$ dans $Q_{\text{AD}}$ (via $\hat H$ évalué en $q_{\text{AD}}$). Cela montre la localité.
Un petit déplacement $(\delta\mathbf r_1,\delta\mathbf r_2)$ permet de rester dans la boule $Q_\text{AD}$ dans $\mathbb R^6$ ($\text{AD}\rightarrow \text{AD}^\prime$ proche de $\text{AD}$), mais le même mouvement déplacerait deux particules simultanément dans des régions de l’espace éloignées à 3D : $\text{A}\rightarrow \text{A}^\prime$ et $\text{D}\rightarrow \text{D}^\prime$. On perdrait la localité.