Notions fondamentales en mécanique quantique

Le cinquième Conseil international de Solvay, en 1927, avait pour thème « Électrons et Photons » et porta principalement sur la mécanique quantique. 17 des 29 personnalités présentes à ce congrès étaient ou allaient devenir prix Nobel…

C’est à cette occasion qu’eurent lieu les échanges entre les représentants de l’« école de Copenhague » (Bohr, Heisenberg, Ehrenfest, etc.), partisans d’une mécanique quantique probabiliste, et les adeptes d’une approche déterministe (Einstein, Schrödinger, de Broglie notamment). Ce fut le début d’une longue controverse d’une vingtaine d’années entre les deux principaux protagonistes, Bohr et Einstein.

Aujourd’hui, l’interprétation de Copenhague est le cadre de référence le plus couramment enseigné, même si d’autres lectures (décohérence, réaliste, informationnelle…) gagnent du terrain.
Les lignes qui suivent en résument brièvement les axiomes et en illustrent quelques conséquences fondamentales, avec un prisme information quantique.

Source : Knee, G. C. « Isolation of the Conceptual Ingredients of Quantum Theory by Toy Theory Comparison », mémoire de Master of Science, Imperial College London, soutenu le 20 septembre 2010 🌐

Un jeu d’axiomes

L’interprétation de la mécanique correspondant à l’école de Copenhague, repose sur un jeu d’axiomes¹ :

Information quantique

Le bit classique

Un bit est la plus petite unité d’information : il distingue entre deux possibilités (le résultat d’un pile ou face, l’état marche/arrêt d’une lampe, le niveau de tension haut/bas dans un circuit, etc.). On note habituellement ces possibilités « zéro logique » et « un logique » : $0, 1$.

Pour représenter plus d’information, on considère une chaîne de bits : avec $n$ bits, on a $2^n$ possibilités (par exemple, pour 3 bits : $000,001, \dots,111$).

Le qubit

L’analogue quantique du bit est le qubit. C’est le système quantique non trivial le plus simple. À l’issue d’une mesure, il distingue également deux possibilités, correspondant aux éléments d’une base orthonormale de l’espace de Hilbert à deux dimensions $\mathcal{H}_2$.

On note $\lvert0\rangle$ et $\lvert1\rangle$ les deux vecteurs de base. On peut les réaliser physiquement de plein de façons : le premier et deuxième niveau d’énergie d’un atome d’hydrogène, le spin haut et le spin bas d’une particule de spin $1/2$, la polarisation horizontale et verticale d’un photon, etc.

Une autre différence importante est qu’on peut tout à fait mesurer le qubit dans une direction qui ne distingue pas $|0\rangle$ de $|1\rangle$.

On identifie deux états qui ne diffèrent que par une phase globale étant donné qu’ils produisent des prédictions physiques identiques. Cela permet de spécifier un qubit par un poids relatif et une phase relative. En ne considérant que des poids égaux dans la superposition, on peut écrire : $$|\psi\rangle = \frac{|0\rangle+\mathrm{e}^{\mathrm{i}\theta} |1\rangle}{\sqrt{2}}$$

Les cas particuliers $\theta=0$ et $\theta=\pi$ donnent respectivement les deux états suivants : $$|+\rangle = \frac{|0\rangle + |1\rangle}{\sqrt{2}}$$ $$|-\rangle = \frac{|0\rangle - |1\rangle}{\sqrt{2}}$$

Il est possible de réaliser une mesure distinguant $|+\rangle$ de $|-\rangle$ en choisissant l’observable $$\hat X \;=\; |+\rangle\langle+| \;-\; |-\rangle\langle-| $$

Contrairement au cas classique, le résultat d’une mesure n’est pas toujours entièrement déterminé par la mesure elle-même et l’état $|\psi\rangle$.

L’information contenue dans un système binaire classique est quantifiée par un bit, soit la quantité nécessaire pour spécifier complètement l’un des deux états possibles. En revanche, pour un état quantique, les coefficients complexes $\alpha$ et $\beta$ peuvent varier de façon continue, de sorte qu’il faudrait une quantité infinie d’information classique pour décrire exactement un qubit.

Matrice densité

La condition de normalisation $\langle\psi|\psi\rangle=1$ entraîne que la trace de la matrice densité vaut un ($\mathrm{Tr}\,\rho_\psi = 1$).

Fidélité

Orthogonalité

État pur et état mixte

Il existe de nombreuses décompositions convexes d’un état mixte : par exemple, l’état mixte maximal

$$ \rho \;=\;\tfrac12\bigl(|0\rangle\langle0| + |1\rangle\langle1|\bigr) \;=\;\tfrac12\bigl(|+\rangle\langle+| + |-\rangle\langle-|\bigr) \;=\;\tfrac{\mathbb{I}}2 $$

Un état mixte ne peut pas s’écrire comme une somme d’états de base à poids complexes.

La différence sémantique entre un état « pur » et un état « mixte » tient au fait que l’incertitude pour le premier est une incertitude purement quantique, tandis que pour le second une part d’incertitude classique est introduite. Un état mixte apparaît si l’on prépare un état quantique en fonction du résultat d’un pile ou face classique, en assignant un certain état pour pile et un autre pour face. On peut aussi interpréter cette incertitude classique comme une forme d’erreur expérimentale.

Sphère de Bloch

Il existe une représentation géométrique élégante des qubits qui facilite grandement la visualisation des opérations de mesure, d’évolution et de similarité des états dans l’espace de Hilbert.

Dans la représentation par matrice densité d’un état pur, on compte à première vue deux coefficients complexes, soit quatre nombres réels. La condition de normalisation (trace = 1) en élimine un. Il reste donc trois degrés de liberté réels pour un état mixte. Et comme on a vu que deux états purs ne se différentiant que par une phase globale sont en fait identiques, il ne reste que deux degrés de liberté pour un état pur². Cela permet de représenter les états purs sur la surface d’une sphère et les états mixtes dans son intérieur.

Grâce à ce vecteur, tout qubit peut être visualisé comme un point de la sphère de Bloch :

• les états purs correspondent aux points de la surface ;
• les états mixtes se situent à l’intérieur ;
• deux états orthogonaux apparaissent comme des points diamétralement opposés.

Par construction, les vecteurs propres des matrices de Pauli occupent trois paires de points antipodaux sur la sphère : $$\hat X|+\rangle = |+\rangle,\quad \hat X|-\rangle = -|-\rangle$$ $$\hat Y|{+}\mathrm{i}\rangle = |{+}\mathrm{i}\rangle=\frac{|0\rangle+\mathrm{i}|1\rangle}{\sqrt{2}},\quad \hat Y|{-}\mathrm{i}\rangle = -|{-}\mathrm{i}\rangle=\frac{|0\rangle-\mathrm{i}|1\rangle}{\sqrt{2}}$$ $$\hat Z|0\rangle = |0\rangle,\quad \hat Z|1\rangle = -|1\rangle$$

Chaque paire de vecteurs propres est une base de l’espace de Hilbert qui définit un axe orthogonal dans la sphère de Bloch.

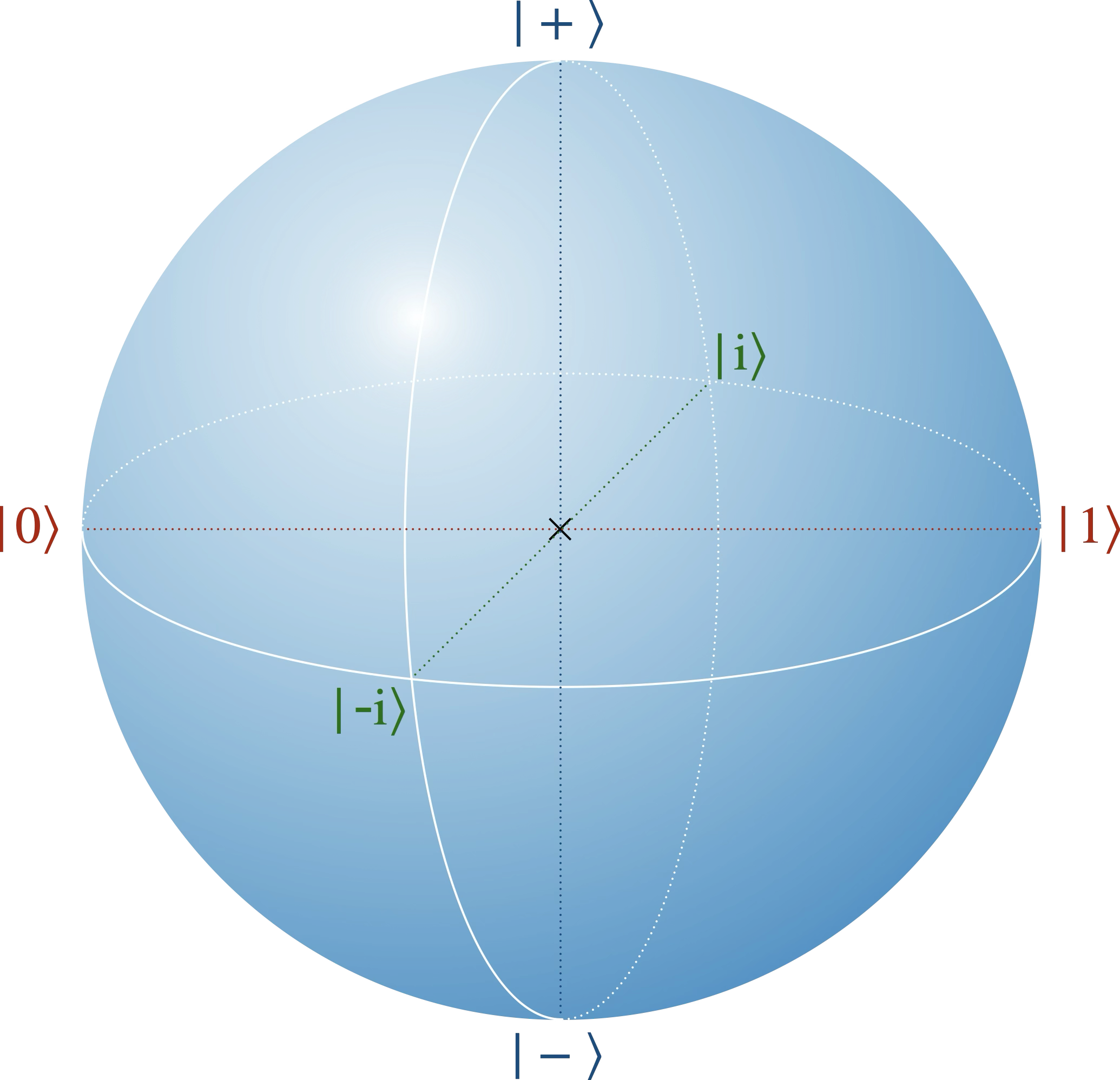
Attention, ça ne veut pas dire que ces trois bases sont orthogonales (ça n’aurait pas de sens puisque chacune est complète) ; elles sont mutuellement non biaisées³ (c’est ça que traduit géométriquement les axes orthogonaux de la sphère de Bloch).

Par combinaison convexe, on fait passer les états purs situés sur la surface de la sphère de Bloch vers des états mixtes à l’intérieur de celle‑ci. L’état maximalement mixte, $\mathbb{I}/2$, se situe au centre de la sphère de Bloch.

Paire de Qubits

Lorsqu’il faut décrire plusieurs systèmes quantiques simultanément, on a recours au produit tensoriel $\otimes$. Supposons, par exemple, qu’on souhaite modéliser à la fois un qubit situé à La Rochelle et un autre à Paris ; on écrit alors $$ |\psi\rangle_{\text{La Rochelle}}\;\otimes\;|\phi\rangle_{\text{Paris}} $$ où $|\psi\rangle$ désigne l’état du premier qubit et $|\phi\rangle$ celui du second. Une fois qu’un ordre conventionnel est adopté, il est d’usage de supprimer les indices géographiques (et même de fusionner les deux kets en un seul) : $$ |\psi\rangle_{\text{La Rochelle}}\otimes|\phi\rangle_{\text{Paris}} \;=\; |\psi\rangle\otimes|\phi\rangle \;=\; |\psi\phi\rangle $$

Cette expression est appelée un état produit ; elle vit dans l’espace de Hilbert tensoriel $H_1\otimes H_2$. Ainsi, si $|\psi\rangle\in H_1$ possède la base $\{|L\rangle,|R\rangle\}$ et $|\phi\rangle\in H_2$ la base $\{|P\rangle,|S\rangle\}$, alors $|\psi\rangle\otimes|\phi\rangle$ appartient à $H_1\otimes H_2$ et la base combinée devient $\{|LP\rangle,|LS\rangle,|RP\rangle,|RS\rangle\}$.

De même qu’un qubit unique peut passer par une porte (unitaire), un état produit peut être soumis à l’action d’un opérateur tensoriel $$ \bigl(\hat A_{\text{La Rochelle}}\otimes\hat B_{\text{Paris}}\bigr)\, |\psi\rangle\otimes|\phi\rangle $$ Si l’on prend $\hat A=\mathbb{I}$, on agit uniquement sur le qubit de Paris ; si c’est $\hat B=\mathbb{I}$, on agit seulement sur celui de La Rochelle.

La base computationnelle $\{|0\rangle,|1\rangle\}$ d’un qubit se prolonge naturellement en une base de l’espace bipartite : $\{|00\rangle,\;|01\rangle,\;|10\rangle,\;|11\rangle\}$. Un état général de deux qubits est donc une combinaison linéaire de ces quatre kets.

On remarque que l’état de Bell ne contient pas les « termes croisés » $|01\rangle$ et $|10\rangle$ (leurs poids sont nuls). Il est donc impossible de l’écrire comme produit de deux qubits séparés ! Les états intriqués comme celui‑ci jouent un rôle central dans la plupart des protocoles de l’information quantique.

Non-clonage quantique

Maintenant qu’un espace produit bipartite a été introduit, on peut l’utiliser pour illustrer certains traits particulièrement surprenants de la mécanique quantique.

Supposons que l’on veuille copier – cloner – un état quantique. Un cloneur universel opère simultanément sur un qubit de données $|\psi\rangle$ et sur un qubit ancillaire initialisé dans un état fixe (par exemple l’état « vierge » $|0\rangle$), de sorte que l’état final soit le produit de deux exemplaires du qubit de données :

$$U\,|\psi\rangle|0\rangle \;=\; |\psi\rangle|\psi\rangle$$

et, par le même procédé, pour tout autre état $|\phi\rangle$ :

$$ U\,|\phi\rangle|0\rangle \;=\; |\phi\rangle|\phi\rangle $$

En prenant le produit scalaire des deux relations précédentes, on obtient :

$$ \langle\psi|\phi\rangle \;=\; \bigl(\langle\psi|\phi\rangle\bigr)^{2} $$

Cette équation n’admet de solution que si les états sont identiques ($\langle\psi|\phi\rangle = 1$) ou orthogonaux ($\langle\psi|\phi\rangle = 0$).

En d’autres termes, la seule procédure qui conserve les produits scalaires (et donc la structure de l’espace de Hilbert) ne peut cloner, au mieux, que des états orthogonaux. Le point crucial est qu’un processus de clonage universel violerait l’évolution unitaire prescrite par l’Axiome 2 : il ne préserverait pas les produits scalaires et ne pourrait donc être représenté par un opérateur unitaire.

Pour cloner un état, l’appareil devrait accéder à toute l’information qui le caractérise sans le perturber. Les états classiques satisfont cette condition : ils peuvent être entièrement déterminés par une quantité finie d’informations et restent intacts lors d’une mesure, de sorte qu’il suffit de les identifier puis de préparer un second système identique. En revanche, un état quantique ne peut être déterminé qu’au prix d’un nombre infini de mesures et, surtout, le processus de mesure le détruit.

Téléportation quantique

La téléportation quantique est un autre phénomène étonnant : il s’accorde parfaitement avec le théorème d’interdiction du clonage, puisqu’on y transfère un état sans jamais en créer une copie supplémentaire.

La description du protocole exige un espace de Hilbert tripartite qu’on peut voir comme le produit tensoriel de trois qubits : $$ \mathcal H = \underbrace{\mathcal H_1 \otimes \mathcal H_2}_{\text{Alice}} \otimes \underbrace{\mathcal H_3}_{\text{Bob}} $$

Alice possède l’état inconnu $|\psi\rangle = \alpha|0\rangle + \beta|1\rangle$ qu’elle veut transmettre à Bob. Aucune ligne « quantique » directe ne relie les deux laboratoires.
Les amplitudes $\alpha$, $\beta$ sont inconnues des deux parties ; un simple message classique ne suffit donc pas.
Alice et Bob partagent toutefois à l’avance une paire intriquée de Bell $|{\rm Bell}\rangle = \frac{1}{\sqrt2}\bigl(|00\rangle+|11\rangle\bigr)$. 

Le système complet est alors initialement $$|{\text{teleport}}\rangle = |\psi\rangle\,|{\rm Bell}\rangle = \frac{1}{\sqrt2}\,|\psi\rangle\bigl(|00\rangle+|11\rangle\bigr)$$ On peut le développer pour bien distinguer la partie Alice et la partie Bob : $$ |{\rm teleport}\rangle = \tfrac1{\sqrt2}\bigl( \alpha {\color{#00AB8E}|00\rangle} {\color{#F27200}|0\rangle} + \alpha {\color{#00AB8E}|01\rangle} {\color{#F27200}|1\rangle} + \beta {\color{#00AB8E}|10\rangle} {\color{#F27200}|0\rangle} + \beta {\color{#00AB8E}|11\rangle} {\color{#F27200}|1\rangle}\bigr) $$

Alice effectue maintenant sur ses deux qubits la mesure définie par l’observable $A=\sum_{i=I,X,Y,Z}\lambda_i P_i$ dont les quatre issues possibles équiprobables sont associées aux projecteurs suivants : $$ \begin{aligned} P_{\mathbb{I}} & =\frac{1}{2}(|00\rangle+|11\rangle)(\langle 00|+\langle 11|) \\ P_X & =\frac{1}{2}(|00\rangle-|11\rangle)(\langle 00|-\langle 11|) \\ P_Y & =\frac{1}{2}(|01\rangle+|10\rangle)(\langle 01|+\langle 10|) \\ P_Z & =\frac{1}{2}(|01\rangle-|10\rangle)(\langle 01|-\langle 10|) \\ \end{aligned} $$

Ces projecteurs vérifient $\sum P_i = \mathbb{I}$ en accord avec l’Axiome 5 et, par la règle de Born (Axiome 3), chaque résultat apparaît avec la probabilité 1/4.

Après la mesure, suivant $\lambda_i$, l’état devient $$|{\rm teleport^\prime_\mathbb{I}}\rangle = {\color{#00AB8E} P_\mathbb{I}}\otimes {\color{#F27200}\mathbb{I}}\,|{\rm teleport}\rangle = {\color{#00AB8E}|{\rm Bell}\rangle}\,\bigl({\color{#F27200}|\psi\rangle}\bigr)$$ $$|{\rm teleport^\prime_\sigma}\rangle = {\color{#00AB8E} P_\sigma}\otimes{\color{#F27200}\mathbb{I}}\,|{\rm teleport}\rangle = {\color{#00AB8E}|{\rm Bell^\prime}\rangle}\,\bigl({\color{#F27200}\sigma|\psi\rangle}\bigr)$$

Avec $\sigma\in{\hat{X},\hat{Y},\hat{Z}}$ (opérateurs de Pauli) et où $|{\text{Bell}^\prime}\rangle$ est l’état de Bell ou une rotation unitaire de l’état de Bell.
Dans 25 % des cas ($P_\mathbb{I}$), le qubit de Bob est déjà le bon et la téléportation est donc déjà achevée ; sinon il en diffère d’un opérateur de Pauli.

Exemple : supposons que $i=X$ :

La partie Alice est bien un état de Bell et Bob se retrouve avec une transformation de l’état à télétransporter.

Alice téléphone alors à Bob et lui envoie deux bits d’information classique pour indiquer son résultat :

• « $00$ » pour un succès direct ($P_\mathbb{I}$) ;
• « $01$ », « $10$ », « $11$ » pour préciser respectivement $\hat{X}$, $\hat{Y}$ ou $\hat{Z}$, l'opérateur de Pauli à utiliser.

Rq : dans notre exemple, Alice envoie $11$.

Bob applique alors la correction sur son qubit avec l’opérateur de Pauli approprié $\sigma$ :

$${\color{#00AB8E}\mathbb{I}}\otimes{\color{#00AB8E}\mathbb{I}}\otimes{\color{#F27200}\sigma}\,|{\text{teleport}^\prime_{\sigma}}\rangle ={ \color{#00AB8E}|{\rm Bell^\prime}\rangle}\,{\color{#F27200}|\psi\rangle}$$

grâce à l’involution de l’opérateur de Pauli $\sigma^2=\mathbb{I}$.