Principe de moindre action

Maupertuis formule ainsi le principe de moindre action en 1744 :

Lorsqu’il arrive quelque changement dans la nature, la quantité d’action, nécessaire pour ce changement, est la plus petite qui soit possible.

Une formulation plus moderne serait la minimisation du transfert d’énergie entre les réservoirs cinétique et potentiel au cours du temps dévolu au trajet entre deux points.

Maupertuis reprenait ainsi le flambeau de Fermat qui avait introduit dès 1657 le principe de moindre temps pour expliquer les trajets des rayons lumineux en optique géométrique.

De tels principes sont dits variationnels car il s’agit d’étudier et minimiser les variations entre deux points.
Leur motivation originelle était métaphysique : par sa perfection, la nature se devait d’être optimale. On trouva ensuite des justifications plus scientifiques…

Conceptuellement, il s’agit d’une démarche descendante (top-down) consistant à fixer un but global et à en déduire ensuite les équations locales qui ont été nécessaires pour l’atteindre. C’est l’inverse de la démarche ascendante (bottom-up) plus familière (car c’est celle enseignée au lycée) qui part des équations locales pour aboutir de proche en proche au global (par un processus itératif).
En mécanique classique par exemple, le local, c’est Newton : on construit la trajectoire complète en intégrant une équation différentielle depuis une position et une vitesse initiale. Et le global, c’est Lagrange ou Hamilton : on fixe deux points et on cherche la bonne trajectoire parmi l’ensemble des trajectoires possibles (celle pour laquelle l’action est stationnaire).

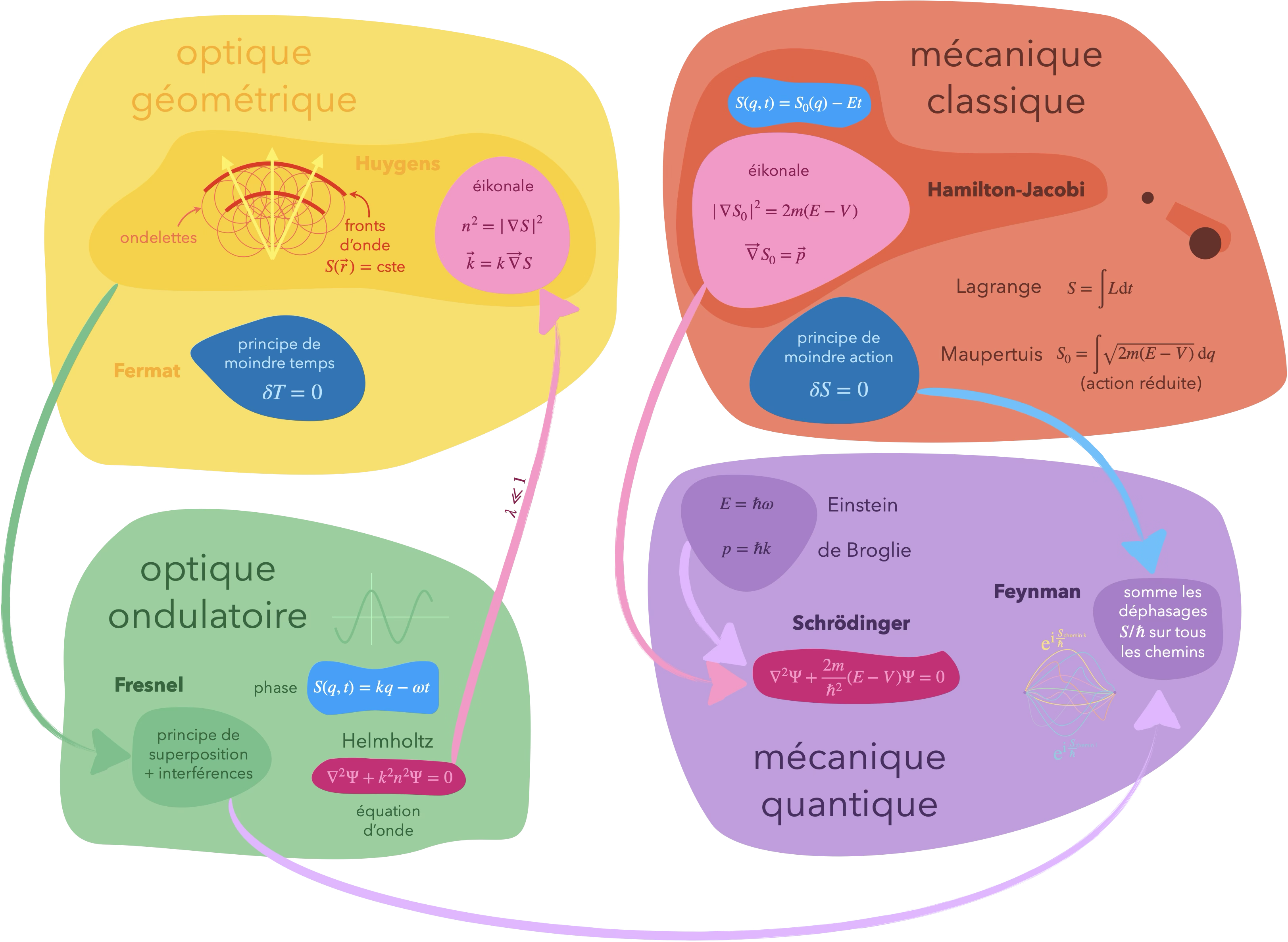
Les théories mécaniques sont progressivement passées d’ascendantes à descendantes. Pour la lumière, c’est l’inverse.

L’évolution des idées en optique est passionnante en soi, mais si on s’y attarde ici, c’est surtout pour l’influence importante qu’elles ont eue sur certains architectes de la mécanique classique puis quantique. Des éléments propres aux théories optiques vont ainsi progressivement percoler en mécanique.

Optique

Principe de moindre temps de Fermat

Reprenons l’idée de Fermat pour déterminer le chemin d’un rayon lumineux réfracté d’un milieu à l’autre. L’idée clé de cette manière de calculer par minimisation est de se donner un point de départ I et un point d’arrivée F et de chercher, parmi toutes les trajectoires possibles les rejoignant, la plus courte.

On constate déjà que si I et F sont dans le même milieu homogène, la trajectoire la plus courte sera le segment de droite [IF] et donc le principe de Fermat prédit bien que la lumière se propage rectilignement dans un milieu homogène.

Et quand le point d’arrivée F est dans un autre milieu que le point de départ I, la prise en compte de l’effet du milieu comme un ralentissement apparent de la vitesse de la lumière (dans un milieu d’indice optique $n$, la lumière voyage à la vitesse $c/n$ où $c$ est sa célérité dans le vide, soit $300\,000$ km/s) permet de retrouver le phénomène de réfraction : la lumière change de direction en passant d’un milieu à l’autre. La déviation est telle que le trajet global sera le moins long possible et donc la partie du trajet dans le milieu d’indice optique supérieur sera plus petite que l’autre.

Dans le programme ci-dessous, les temps de parcours de différents trajets pour rejoindre un point dans l’air à un point dans l’eau sont comparés. Le trajet minimal est déterminé et on montre qu’il respecte la loi de la réfraction de Snell-Descartes.

C’est très élégant, mais n’est-ce pas que cela ? un raffinement calculatoire ? Comment la lumière pourrait-elle aller explorer les différents chemins avant de choisir le moins long ? Cela paraît saugrenu… Du moins du côté particulaire de la description de la lumière, car pour une onde, ce n’est pas si bizarre. Une onde est en effet intrinsèquement la modélisation d’un comportement collectif. Considérer une onde, c’est donc bien considérer différents trajets pris “à la fois”.

Ondelettes de Huygens

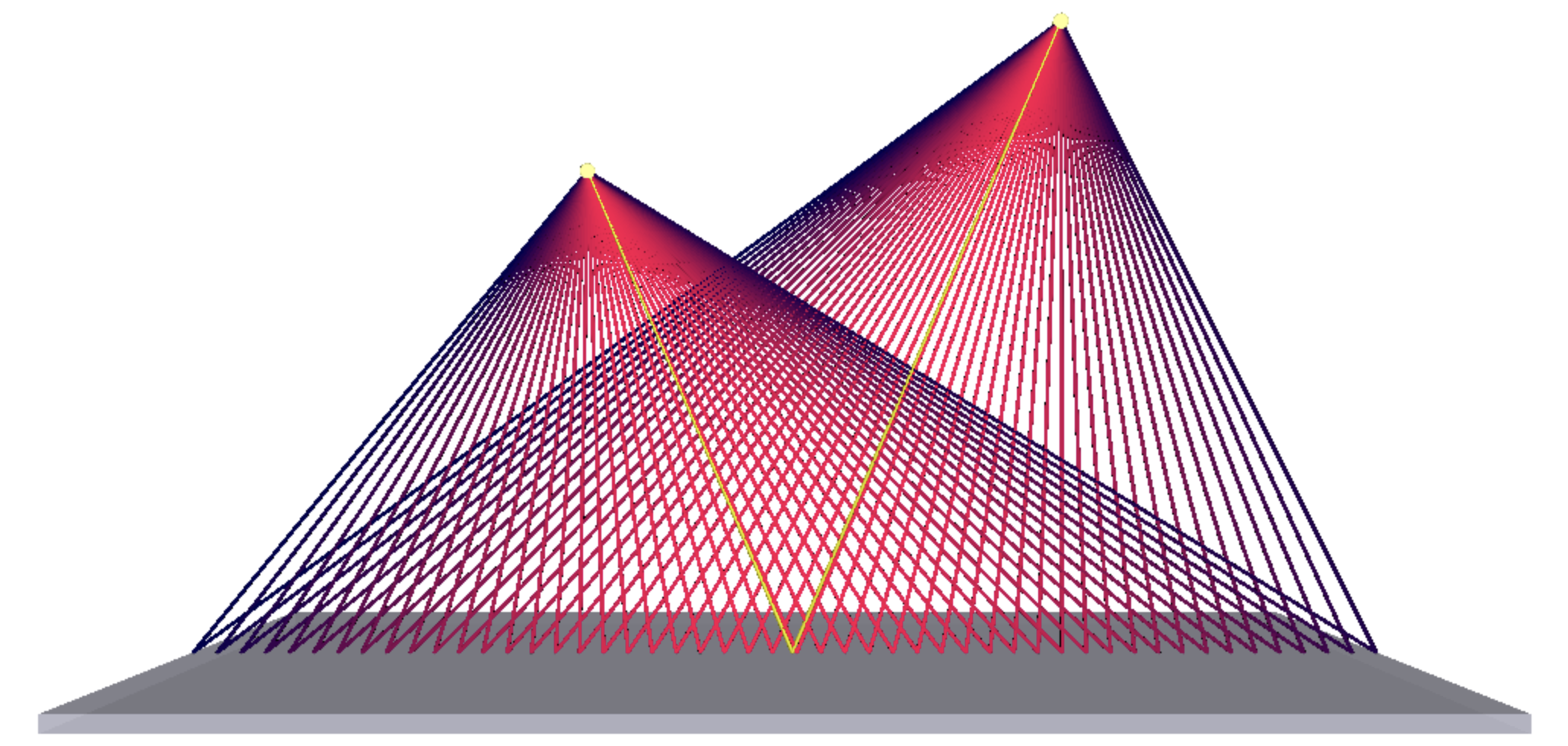
Pour apprivoiser ce mouvement collectif, Huygens a l’idée en 1678 de décrire tout point atteint par la lumière comme la source d’une nouvelle ondelette sphérique qui va se propager depuis ce point. Reconstituer le trajet de la lumière revient alors à regarder où les fronts d’onde de ces ondelettes s’accumulent pour former une enveloppe, le rayon perçant cette enveloppe perpendiculairement.

Huygens parvient avec son principe de superposition à retrouver l’ensemble des prédictions de Fermat. L’optique géométrique tenait donc là deux explications alternatives ; l’une variationnelle et l’autre à base de fronts d’onde.

Pour être plus précis et faciliter le parallèle avec Hamilton ensuite, explicitons les définitions.

Soit l’ensemble des points $q$ jusqu’où la lumière issue d’un point $q_0$ peut traverser en un temps inférieur ou égal à $t$. La frontière de cet ensemble, $\Phi_{q_0}(t)$ est appelé le front d’onde du point $q_0$ après un temps $t$ et regroupe les points que la lumière peut atteindre en un temps $t$ mais pas avant.

Le principe de Huygens peut alors s’exprimer ainsi :
soit $\Phi_{q_0}(t)$ le front d’onde issu du point $q_0$ après un temps $t$. Pour chaque point $q$ de ce front, on considère le front d’onde au temps $s$, $\Phi_{q}(s)$. Alors le front d’onde issu du point $q_0$ après le temps $t+s$, $\Phi_{q_0}(t+s)$ sera l’enveloppe des fronts $\Phi_{q}(s),q\in \Phi_{q_0}(t)$.

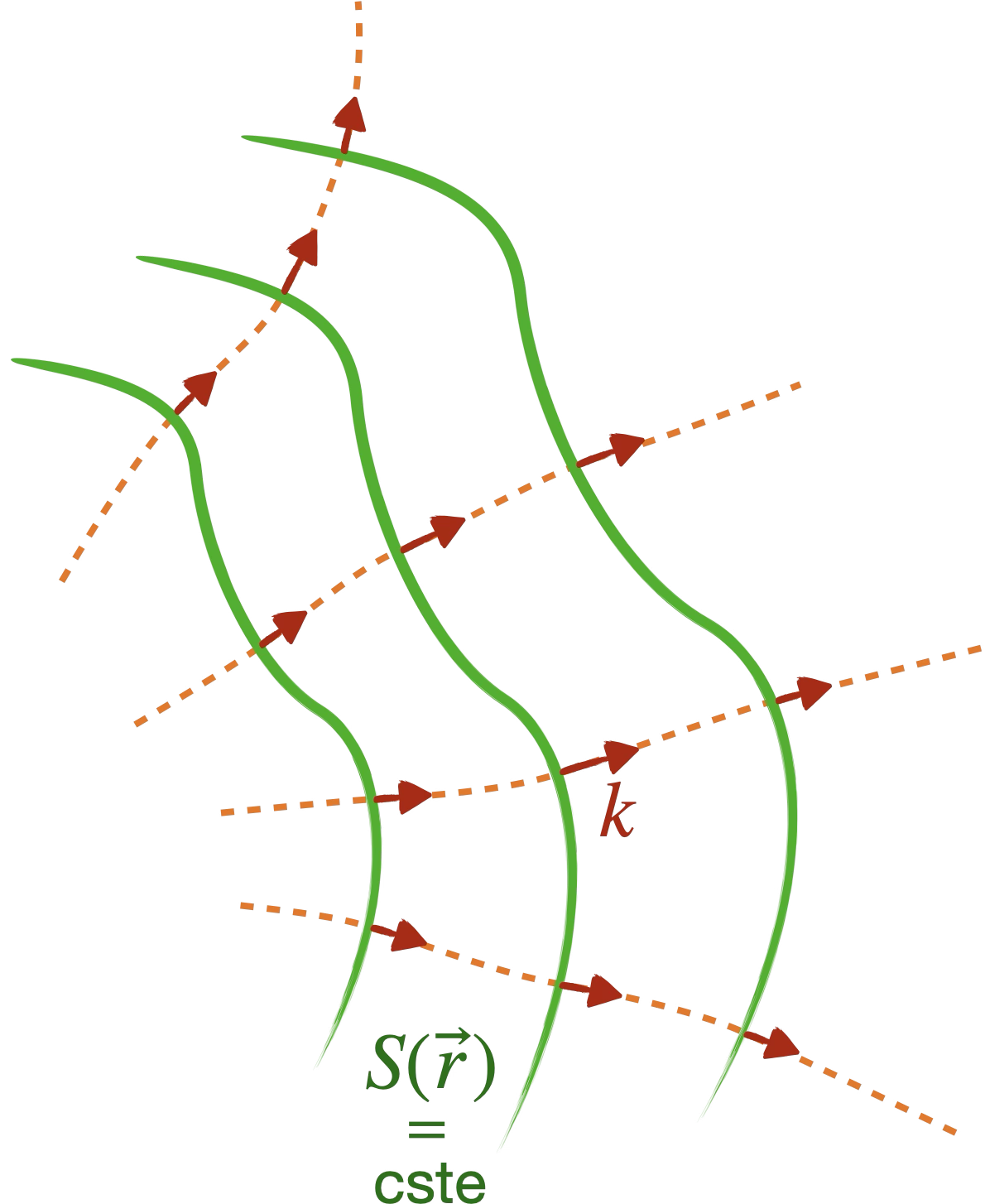
En fixant un point $q_0$, on appelle fonction caractéristique $S_{q_0}(q)$ la fonction qui associe à tout point $q$ le longueur du chemin optique de $q_0$ à $q$.
Les courbes de niveau de la fonction caractéristique ne sont autre que les fronts d’onde.

L’animation ci-dessous montre comment l’enveloppe des fronts d’onde est naturellement déviée lors d’un changement de milieu si la vitesse de propagation change, expliquant ainsi la réfraction.

Même si ses “ondelettes” préfigurent évidemment de véritables ondes, Huygens se contente de modéliser l’optique géométrique avec sa théorie et il s’imagine d’ailleurs les ondelettes s’évanouir partout ailleurs que sur l’enveloppe.

Vers l’optique ondulatoire

En 1803, Young publie un dessin expliquant comment la lumière passant à travers deux fentes étroites donne naissance à des franges alternativement brillantes et sombres sur un écran.

On est encore très proche des ondelettes de Huygens sauf qu’on tourne notre attention sur l’ensemble du réseau plutôt qu’exclusivement sur les enveloppes.

La théorie de Huygens nécessite une superposition de suffisamment de sources pour clairement définir ses fronts d’onde.

Dans l’image précédente, on a additionné des sources sur un petit segment vertical. L’effet de moiré nous donne un aperçu du phénomène de diffraction.

En étirant le segment avec de nouvelles sources, les enveloppes finissent par mieux se définir ; on retrouve une propagation rectiligne (du moins autour de l’axe de symétrie perpendiculaire aux sources).

Si on peut comprendre géométriquement l’apparition de zone brillante par superposition des réseaux d’ondelettes, l’existence de zone parfaitement sombre est plus mystérieuse. Comment des zones éclairées plusieurs fois pourraient-elles se trouver obscurcies ?

Fresnel et la phase

L’ingrédient manquant pour expliquer les interférences est apporté en 1818 par Fresnel  : il donne une phase aux ondelette ! Un traitement mathématique complet devenait possible et Fresnel fut ainsi capable de mettre au point la théorie de la diffraction.

Fresnel s’imagine que la lumière est une vibration transversale de l’éther analogue aux ondes mécaniques décrites au siècle précédent par d’Alembert (1747).
Il donne alors aux ondelettes de Huygens le pouvoir d’interférer grâce à la phase $\phi=\omega t-\vec{k}\cdot\vec{r}$ (avec $\|\vec{k}\|=k=\frac{n \omega}{c}$).

Arago écrira :

Quel est donc le procédé magique qui permet de transformer à volonté la lumière en ombre, le jour en nuit ? Ce procédé excitera plus de surprise encore que le fait en lui-même ; ce procédé consiste à diriger sur le papier, mais par une route légèrement différente, un second rayon lumineux qui, pris isolément aussi, l’aurait fortement éclairé. Les deux rayons en se mêlant semblaient devoir produire une illumination plus vive ; le doute à cet égard ne semblait point permis ; eh bien ! ils se détruisent quelquefois tout à fait et l’on se se trouve avoir créé les ténèbres en ajoutant de la lumière à la lumière.
Un fait neuf exige un mot nouveau. Ce phénomène dans lequel des rayons, en se mêlant, se détruisent tout à fait ou seulement en partie, s’appelle une interférence.

Lumière ou obscurité se déduisent désormais du terme d’interférence entre les différentes sources secondaires en un endroit donné. Et grâce aux interférences, le principe de superposition de Huygens peut maintenant expliquer la diffraction ! En sommant continument les multiples déphasages des ondelettes sur les fronts d’onde¹, Fresnel est capable de prédire précisément les figures de diffraction obtenues dans plusieurs situations.

Aujourd’hui, le principe de superposition moderne mis au point par Fresnel porte le nom de ses deux papas : principe de Huygens-Fresnel.

Fresnel est le grand artisan du basculement de paradigme d’une description corpusculaire de la lumière (dont le géant Newton était le fer de lance) vers une description ondulatoire. Un fervent partisan des particules, Poisson, joua aussi un rôle amusant…
Lorsqu’il éplucha le mémoire de concours de Fresnel, Poisson reprit ses intégrales de diffraction et présenta ses résultats en 1819 devant la commission du « Grand Prix de la Diffraction » de l’Académie des sciences. Les calculs prédisent un point lumineux au centre de l’ombre d’un disque éclairé par une source ponctuelle. Totalement absurde pour un partisan des particules ! Poisson est convaincu qu’il tient là l’argument définitif contre la théorie ondulatoire. Arago qui présidait la commission voulut en avoir le cœur net et monta l’expérience. Il observa alors bien ce qui sera désormais appelée tâche de Fresnel (Arago spot en anglais)² ! L’argument définitif de Poisson fit finalement triompher les ondes³.

Helmholtz

En 1859, Helmholtz résume quasiment toute l’optique en une unique équation d’onde scalaire (d’abord pensée pour l’acoustique avant d’être adaptée à l’optique).

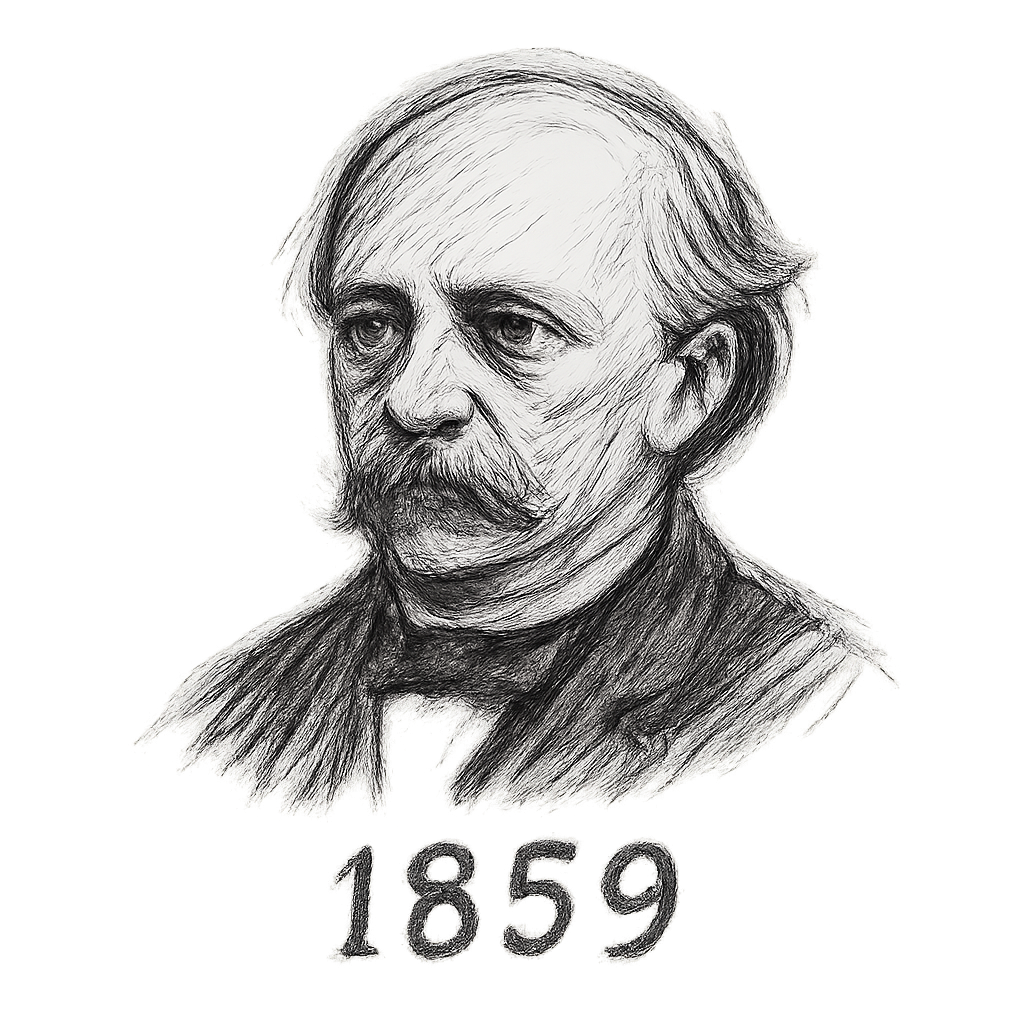
$$\nabla^2 \Psi(\vec{r})+k^2 n^2(\vec{r}) \Psi(\vec{r})=0$$

L’animation ci-dessous est calculée à partir de cette seule équation. Une série verticale de sources sur la gauche, un obstacle sphérique où l’onde vaut zéro et on laisse la magie (ou la physique, c’est selon) opérer.

De l’optique ondulatoire à l’optique géométrique

L’optique géométrique n’est maintenant plus que la limite aux courtes longueurs d’onde de l’optique ondulatoire.

En injectant dans l’équation de Helmholtz une solution de la forme $\Psi(\vec{r})=A(\vec{r}) e^{i k_0 S(\vec{r})}$ (où la phase réduite $S$ et l’amplitude $A$ changent peu sur des distances de l’ordre de $\lambda$) et en ne gardant que le plus grand ordre en $k_0$ (ordre 2), on obtient l’équation éikonale : $|\vec{\nabla} S|^2=n^2(\mathbf{r})$.

La phase totale étant $k_0S(\vec{r})$, on définit le vecteur d’onde $\vec{k}(\vec{r})=\vec{\nabla}\phi=k_0\vec{\nabla}S$. En prenant son carré $|\vec{k}|^2$, on obtient $k_0^2|\vec{\nabla} S|^2=k_0^2 n^2(\vec{r})$. Et donc $|\vec{k}|=\frac{2 \pi}{\lambda_0} n(\vec{r})=\frac{2 \pi}{\lambda(\vec{r})}$. C’est bien la norme attendue pour un vecteur d’onde dans un milieu d’indice $n$ (où la longueur d’onde locale vaut $\lambda=\lambda_0/n$).

Les surfaces de phase constante correspondent à $S(\vec{r})=\text{cste}$. Et comme le gradient d’une fonction scalaire est orthogonal aux surfaces de niveau, $\vec{n} =\vec{\nabla} S$ est la normale au front d’onde.
Puisqu’on a défini $\vec{k}$ comme proportionnel à $\vec{\nabla} S$, le vecteur d’onde est colinéaire à la normale. Sa direction est celle du rayon en optique géométrique.

En paramétrant le trajet par l’abscisse curviligne $s$, on obtient l’équation d’un rayon lumineux : $\frac{d \vec{r}}{d s}=\frac{\vec{k}}{|\vec{k}|}=\frac{\vec{\nabla} S}{n}$.

Faraday et Maxwell

Dès 1845, Faraday a l’intuition que la lumière est une onde électromagnétique. Mais c’est 20 ans plus tard que Maxwell clôt définitivement le chapitre de l’optique classique dans un bouquet final.

Avec lui, la lumière est promue onde vectorielle et elle intègre officiellement le spectre du rayonnement du champ électromagnétique (dont elle ne constitue qu’une toute petite partie), et sa vitesse est maintenant déterminée théoriquement ($c=\frac{1}{\sqrt{\epsilon_0\mu_0}}$).

D’un point de vue théorique, la compréhension scientifique de la lumière est donc partie d’un principe variationnel global pour terminer sur des équations locales (celles d’Helmholtz ou de Maxwell).
La mécanique a fait le chemin inverse, on a d’abord eu les équations de Newton (locales) avant de se tourner vers les principes variationnels.

Mécanique

Bernoulli et la brachystochrone

En 1696, Jean Bernoulli utilise l’optique pour résoudre un problème de mécanique qui chiffonnait les physiciens de l’époque, le problème de la brachystochrone.

Quelle courbe dévalée par un point matériel pesant sans frottement ni vitesse initiale permet de rejoindre le plus vite le point de départ à un point d’arrivée fixé (en aval par rapport au champ de pesanteur supposé uniforme) ?

Bernoulli a en tête le principe de Fermat : le trajet le plus court entre les deux points est celui que suivrait la lumière. Et pour la trajectoire courbée, il fait l’analogie avec les mirages : il découpe verticalement l’espace en strates d’indices différents faisant varier la vitesse. La conservation de l’énergie lui donne une vitesse $v=\sqrt{2gy}$ à la strate d’altitude $y$ et la loi de réfraction selon le principe de Fermat lui assure que $\frac{\sin\theta}{v}=\text{cste}$ et donc $\frac{\theta}{\sqrt{y}}=\text{cste}$ où $\theta$ est l’angle par rapport à la verticale. Il réussit ainsi à démontrer que la courbe optimale est une cycloïde dont la tangente initiale est verticale au départ et qui est engendrée par un cercle dont le diamètre est la descente maximale du point.

La raison pour laquelle $\frac{\theta}{\sqrt{y}}=\text{cste}$ correspond à une cycloïde est donnée dans cette vidéo de 3Blue1Brown.

Et le petit programme ci-dessous permet de tester manuellement différentes courbes et vérifier que le temps minimal est obtenu quand on s’approche de la cycloïde (courbe jaune).

La formulation de ce problème est typiquement variationnelle et cela en fait un tremplin (cycloïdique) vers les théories à venir (surtout que toutes les stars du moment s’y confrontent et proposent une solution : le frère de Jean, Jacques Bernoulli, L’Hôpital, Leibniz, Newton, etc.).

En jetant un pont entre l’optique et la mécanique pour résoudre la brachistochrone, Bernoulli préfigure les futurs travaux de Hamilton.

Maupertuis

En 1744, Maupertuis porte dans le domaine de mécanique l’idée de Fermat d’un principe variationnel permettant de déterminer le trajet des rayons lumineux. Il s’agit maintenant d’obtenir la trajectoire d’un système entre deux points en extrémisant une certaine grandeur : l’action.

Pour Maupertuis, l’action c’est $S_M=\int_{A\rightarrow B}mv\mathrm{d}s$ où $s$ est l’abscisse curviligne sur la trajectoire. Anachroniquement, on peut transformer $S_M$ en $\int_{A\rightarrow B}2T\mathrm{d}t$ où $T$ est l’énergie cinétique et minimiser l’action de Maupertuis revient alors à minimiser l’énergie cinétique au cours du temps à énergie totale fixée.
L’action trouve déjà là sa dimension définitive d’une énergie multipliée par une durée, ou une quantité de mouvement multipliée par une distance.

Lagrange

Un élève de Jean Bernoulli, Euler (le 🐐 des mathématiques), met au point le calcul des variations à partir de considérations géométriques et généralise ainsi les méthodes mises au point pour résoudre le problème de la brachistochrone.

Lagrange donne sa forme actuelle à ce nouveau type de calcul avec une approche purement analytique et il introduit les coordonnées généralisées $q_i$ (qui en plus des positions habituelles peuvent être des positions relatives, des angles, etc.) et la variable temps que n’utilisait pas Maupertuis.

La définition lagrangienne de l’action généralise celle de Maupertuis : $S_L=\int_{t_1}^{t_2} L(q, \dot{q}, t) \mathrm{d} t$ où $L$, le lagrangien, vaut $T-V$, la différence entre l’énergie cinétique et l’énergie potentielle.

Le principe de stationnarité $\delta S_L= 0$ pour des extrémités fixées en temps conduit aux équations d’Euler-Lagrange :
$$\frac{\mathrm{d}}{\mathrm{d} t}\frac{\partial L}{\partial \dot{q}_i} - \frac{\partial L}{\partial q_i} = 0$$

Dorénavant, le lagrangien sera au cœur de la physique moderne : toute théorie commence par se chercher un lagrangien puisque tout découle de lui. Un des plus grands achèvements humains est ainsi l’établissement du lagrangien du modèle standard qui réunit toute la physique hormis la gravité.

Le lagrangien de l’optique géométrique

Le principe de moindre temps et le principe de moindre action sont deux principes variationnels. Dans l’optique géométrique de Fermat, l’action correspond à la durée du trajet entre le point de départ et le point d’arrivée. Mais qui joue le rôle du temps chez Fermat ? Répondre revient à déterminer le “lagrangien” de l’optique géométrique.

Supposons que le rayon se déplace dans un plan $(x,z)$ où $z$ serait l’axe optique ou l’axe de propagation. Le temps de parcours vaut alors $T=\frac1c \int_1^2 n(x,z)\mathrm{d}\ell=\frac1c \int_1^2 n(x,z)\sqrt{\mathrm{d}x^2+\mathrm{d}z^2}=\frac1c \int_1^2 n(x,z)\sqrt{1+\frac{\mathrm{d}x^2}{\mathrm{d}z^2}}\,\mathrm{d}z=\int_1^2\mathcal{L}(x,\tilde{x},z)\,\mathrm{d}z$ où on on note $\tilde{x}\equiv\frac{\mathrm{d}x}{\mathrm{d}z}$.

Le rôle du temps de la mécanique est donc joué par la coordonnée $z$ selon l’axe de propagation, $x$ garde son rôle et la vitesse $\dot{x}$ devient l’inclinaison du rayon par rapport à la direction de propagation $\mathrm{d}x/\mathrm{d}z$. Notons que le lagrangien de l’optique a la dimension de l’inverse d’une vitesse plutôt que d’une énergie.

L’équation d’Euler-Lagrange s’écrit $\frac{\mathrm{d}}{\mathrm{d}z}\left(\frac{\partial\mathcal{L}}{\partial \tilde{x}}\right)=\frac{\partial\mathcal{L}}{\partial x}$ et on tire du lagrangien $\frac{\partial\mathcal{L}}{\partial \tilde{x}}=\frac{n(x,z)\tilde{x}}{c\sqrt{1+\tilde{x}^2}}$.
Supposons que l’indice ne dépende pas de $x$ : $n(x,z)=n(z)$. On a alors $\frac{\partial\mathcal{L}}{\partial x}=0$ et donc $\frac{\partial\mathcal{L}}{\partial \tilde{x}}$ est une constante en $z$ conservée le long de l’axe de propagation.

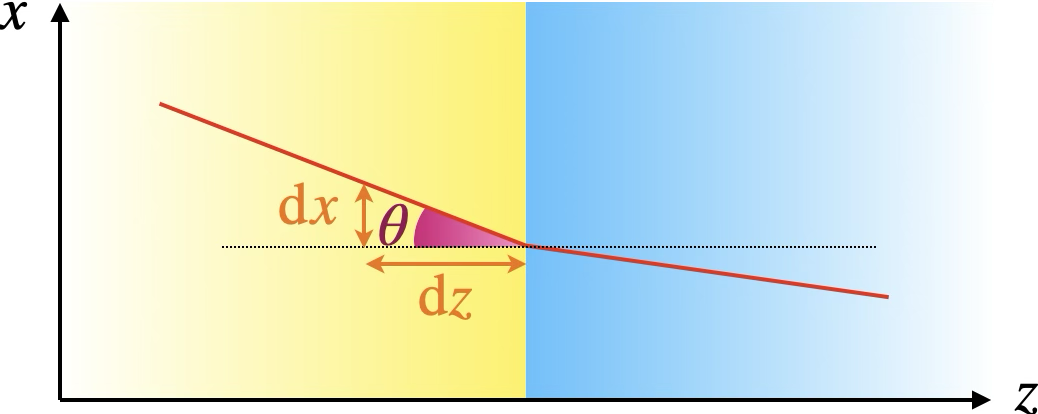
On constate sur le schéma que $\tilde{x}=\tan\theta$ et donc $\frac{\tilde{x}}{\sqrt{1+\tilde{x}^2}}=\sin\theta$. La constance de $\frac{\partial\mathcal{L}}{\partial \tilde{x}}$ selon $z$ implique donc celle de $n(z)\sin\theta$. On a retrouvé la loi de Snell-Descartes de la réfraction !

Hamilton

Hamilton a pavé la voie pour la transition de la mécanique classique à la mécanique quantique.

On passe de la formulation de Lagrange à celle d’Hamilton en définissant les moments $p_i=\partial L / \partial \dot{q}_i$ et en utilisant la transformée de Legendre $H(q, p, t)=\sum_i p_i \dot{q}_i-L$. Cela permet de remplacer la variable $\dot{q}$ par le moment conjugué $p$ (ou impulsion).

L’espace des configurations (l’espace des coordonnées ${q}$) où prend racine la mécanique lagrangienne est ainsi déménagée vers l’espace des phases $(q,p)$ où l’impulsion $p$ est considérée comme une coordonnée libre au même titre que $q$ (ce qui ne pouvait pas être le cas de $\dot{q}=\frac{\mathrm{d}q}{\mathrm{d}t}$)⁴.

L’action devient pour Hamilton $S_H=\int_{t_1}^{t_2}\left(\sum_i p_i \dot{q}_i-H\right) \mathrm{d} t$.
La stationnarité $\delta S_H = 0$, pour des extrémités fixes en $(q,t)$ fournit les équations canoniques :
$\dot{q}_i=\frac{\partial H}{\partial p_i}, \quad \dot{p}_i=-\frac{\partial H}{\partial q_i}$.

L’espace des phases est déjà “quantum-ready” : les transformations canoniques entre $q$ et $p$ seront les mêmes, les crochets de Poisson (oui le même que la tâche) préfigurent les commutateurs, les symétries d’évolution à la Noether s’expriment naturellement, etc.

Hamilton-Jacobi

Le principe de moindre action à la Lagrange consistant à chercher un chemin dans l’espace des configurations qui rende stationnaire l’action est tout à fait analogue au principe de Fermat.
Huygens ayant réussi à reproduire les résultats de Fermat avec ses ondelettes, Hamilton se demande si on ne pourrait pas trouver une formulation équivalente en mécanique. Une mécanique à base d’ondelettes et de fronts d’onde !

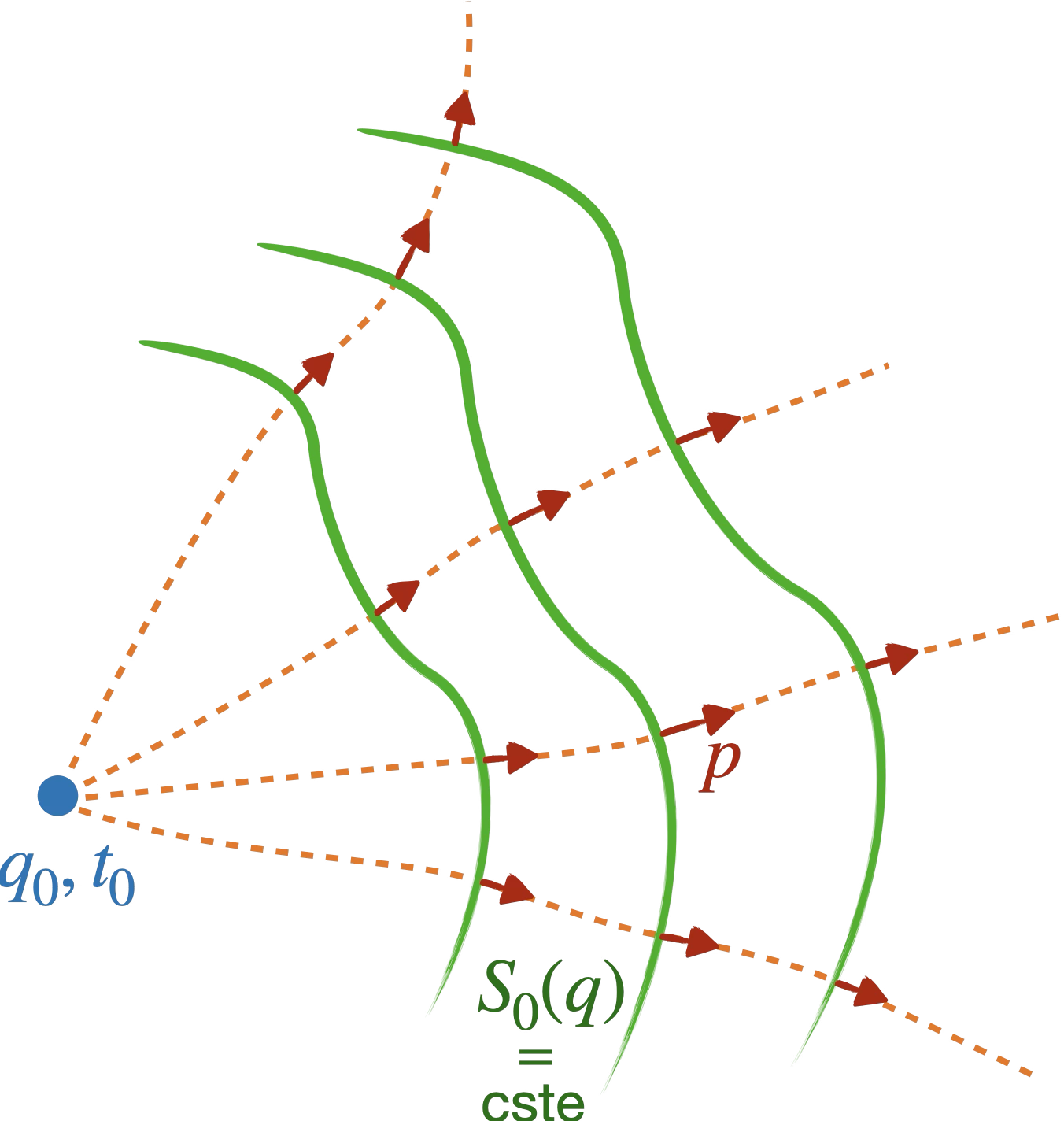
Hamilton y parvient en envisageant l’action sous un nouvel aspect. Plutôt que de fixer les points de départ ($q_0,t_0$) et d’arrivée ($q_F,t_F$), il laisse ce dernier libre ($q,t$). Il obtient alors :

• $\displaystyle\frac{\partial S}{\partial q}=p$
• $\displaystyle\frac{\partial S}{\partial t}=-H$ (équation de Hamilton-Jacobi)

Dans le cas d’un système conservatif, on déduit de l’équation de Hamilton-Jacobi⁵ : $$S(q, t)=S_{0}(q)-E t$$ Hamilton a alors l’intuition géniale d’y voir une phase $\phi(\vec{r},t) = \vec{k} \cdot\vec{r}-\omega t$. Mais sa quête n’est pas celle d’une mécanique purement ondulatoire (il faudra attendre Schrödinger pour ça), il souhaite la “forme Huygens” de l’équivalence entre la mécanique et l’optique géométrique.

Par analogie avec la limite de l’optique ondulatoire aux petites longueurs d’onde et le principe de Huygens, on peut identifier $S_{0}(q)$ avec la fonction caractéristique donnant la longueur du chemin optique de $q_0$ à $q$.
Comme $\partial S_0(q) / \partial q=p$, le vecteur normal à la surface $S_0(q)=\text{cst}$, $\vec{\nabla} S_0(q)$ n’est autre que le vecteur impulsion $\vec{p}$.

La trajectoire mécanique suit les rayons (donnés par l’impulsion) normaux aux fronts d’onde constitués par les surfaces d’action réduite constante !

Schrödinger résume les travaux d’Hamilton ainsi :

Le principe variationnel de Hamilton se trouve correspondre au principe de Fermat pour la propagation d’une onde dans l’espace des configurations (espace des q), et l’équation de Hamilton–Jacobi exprime le principe de Huygens pour cette propagation. Malheureusement, cette conception puissante et d’une importance majeure de Hamilton est, dans la plupart des relectures modernes, dépouillée de son magnifique habit — jugé superflu — au profit d’une représentation plus terne de la correspondance analytique.

L’admiration que voue Schrödinger à Hamilton a été récompensée puisque les travaux d’Hamilton se sont révélés essentiels dans la quête de Schrödinger d’une équation d’onde quantique.

Si Hamilton jette les base de la révolution quantique, les lubies géométriques de Jacobi préfigurent une autre révolution du 20^e siècle, celle de la relativité générale.
Il transforme en effet la recherche d’une trajectoire minimisant l’action en la recherche d’une géodésique dans l’espace des configurations ! Pour un système à énergie fixée, il réécrit ainsi l’action réduite comme $W=\int_{q_1}^{q_2}p^i\mathrm{d}q_i$ en $\int_{q_1}^{q_2}ds_J$ en introduisant la métrique de Jacobi : $\mathrm{d}s_J^2 = 2(E-V(q)) g_{i j}(q) \mathrm{d} q^i \mathrm{d} q^j$ (où $g_{ij}$ est une métrique riemannienne). Le principe de Maupertuis devient alors un théorème géométrique.

L’avènement de la mécanique quantique

Planck

À la fin du 19^e siècle, réussir à modéliser l’énergie libérée par un corps noir (une cavité dont les seules émissions de rayonnement sont thermiques) en fonction de la fréquence est une énigme qui résiste au physicien.

Le nombre de modes de vibration augment avec la fréquence et à l’équilibre thermique, chaque mode doit recevoir la même énergie, proportionnelle à la température. Moralité, la densité d’énergie aux grandes fréquences explose, c’est la catastrophe ultraviolette ! Bien sûr, la théorie est en violente contradiction avec l’expérience qui présente zéro catastrophe.

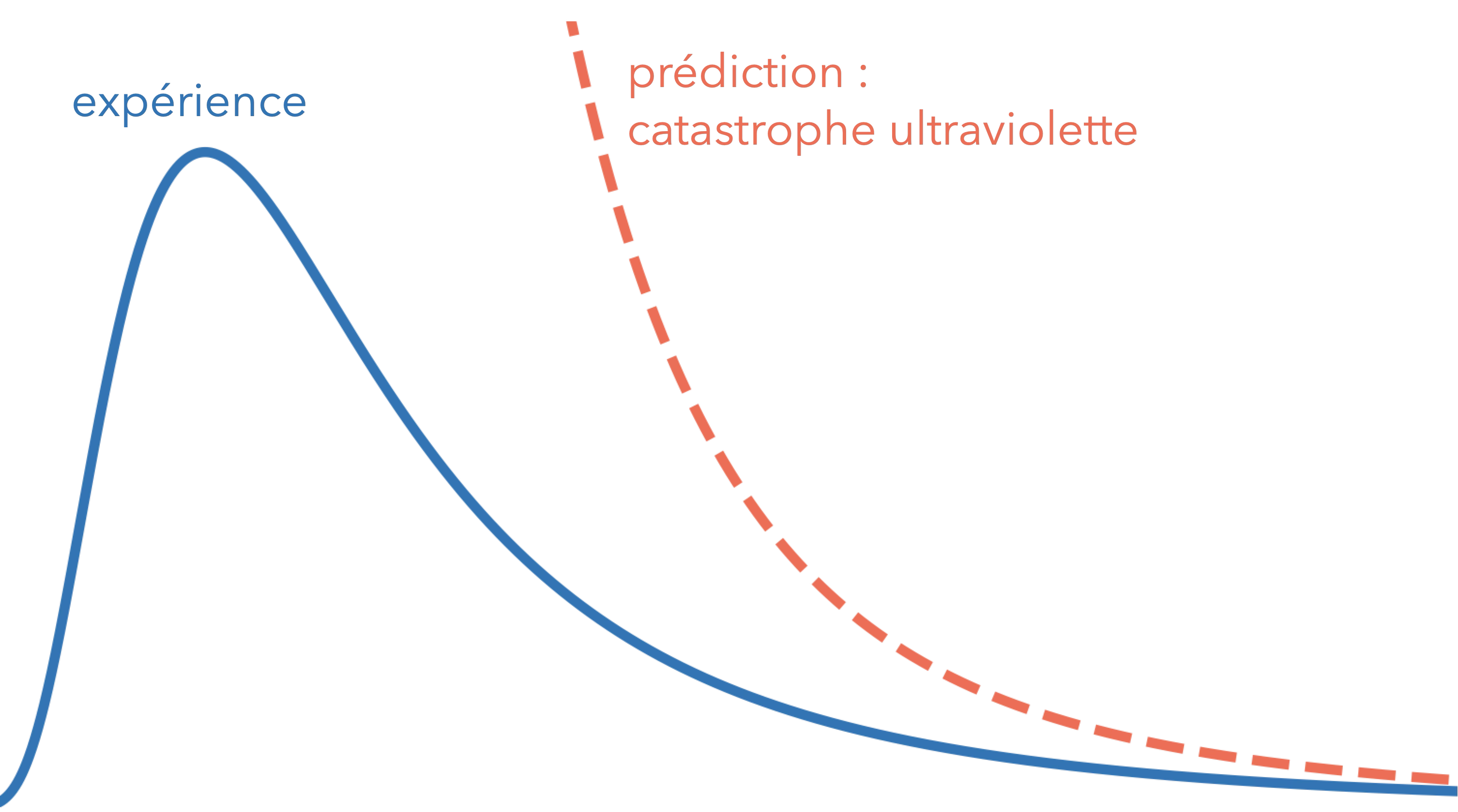
Pour tenter de résoudre le problème, Planck utilise ce qu’il pense être un expédiant provisoire : il introduit une discrétisation, un pas $h$ dont il compte bien se débarrasser ensuite en le faisant tendre vers zéro.

Et ça marche ! Il obtient la courbe attendue du corps noir. Mais à son grand désarroi, il n’arrive pas à se débarrasser de $h$. En le faisant tendre vers zéro, il perd la courbe. Et l’accord avec les résultats expérimentaux lui fixent même une valeur pour son petit pas : $\pu{6,63E-34 J*s}$. Car oui, ce pas de discrétisation (qui deviendra la constante de Planck $h$) a la dimension d’une action, c’est un quantum d’action !

Pour la première fois, une modélisation de la nature s’avère fondamentalement discontinue et c’est l’action qui refuse de se faire découper infiniment.

de Broglie

Dans son élan fabuleux de 1905, Einstein explique l’effet photoélectrique en discrétisant la lumière en photons d’énergie $E=h\nu$, généralisant l’idée de Planck au rayonnement.

De Broglie comprend alors que la formule $E=h\nu$ n’est pas réservée aux photons puisque le rayonnement échange de l’énergie avec la matière.

Il écrira :

Après une longue méditation et réflexion solitaire, j’ai subitement eu l’idée durant l’année 1923, que la découverte faite par Einstein en 1905 doit être généralisée par extension à toute particule de matière et singulièrement l’électron.

Avec ce quantum d’énergie proportionnel à la fréquence, on associe de fait une caractéristique ondulatoire à la matière. De Broglie pousse cette dualité onde-corpuscule un cran plus loin en lui donnant aussi une longueur d’onde qu’il relie à la quantité de mouvement : $\lambda=\frac{h}{p}$.

On a maintenant un lien direct entre le $\int n\,\mathrm{d}q$ de Fermat et le $\int p\,\mathrm{d}q$ de Maupertuis (l’action réduite d’Hamilton) : en appelant $v$ la vitesse de l’onde dans le milieu, $n=\frac{c}{v}=\frac{c}{\lambda\nu}=\frac{c}{\frac{h}{p}\frac{E}{h}}=\frac{pc}{E}$. Et donc $\int n\,\mathrm{d}q=\frac{c}{E}\int p\,\mathrm{d}q$.

De Broglie parvient avec sa relation à donner du sens aux orbites quantifiées de l’atome de Bohr : l’électron en orbite évolue sur une trajectoire fermée et maintenant qu’on peut lui associer une longueur d’onde, un système d’ondes stationnaires se met en place.

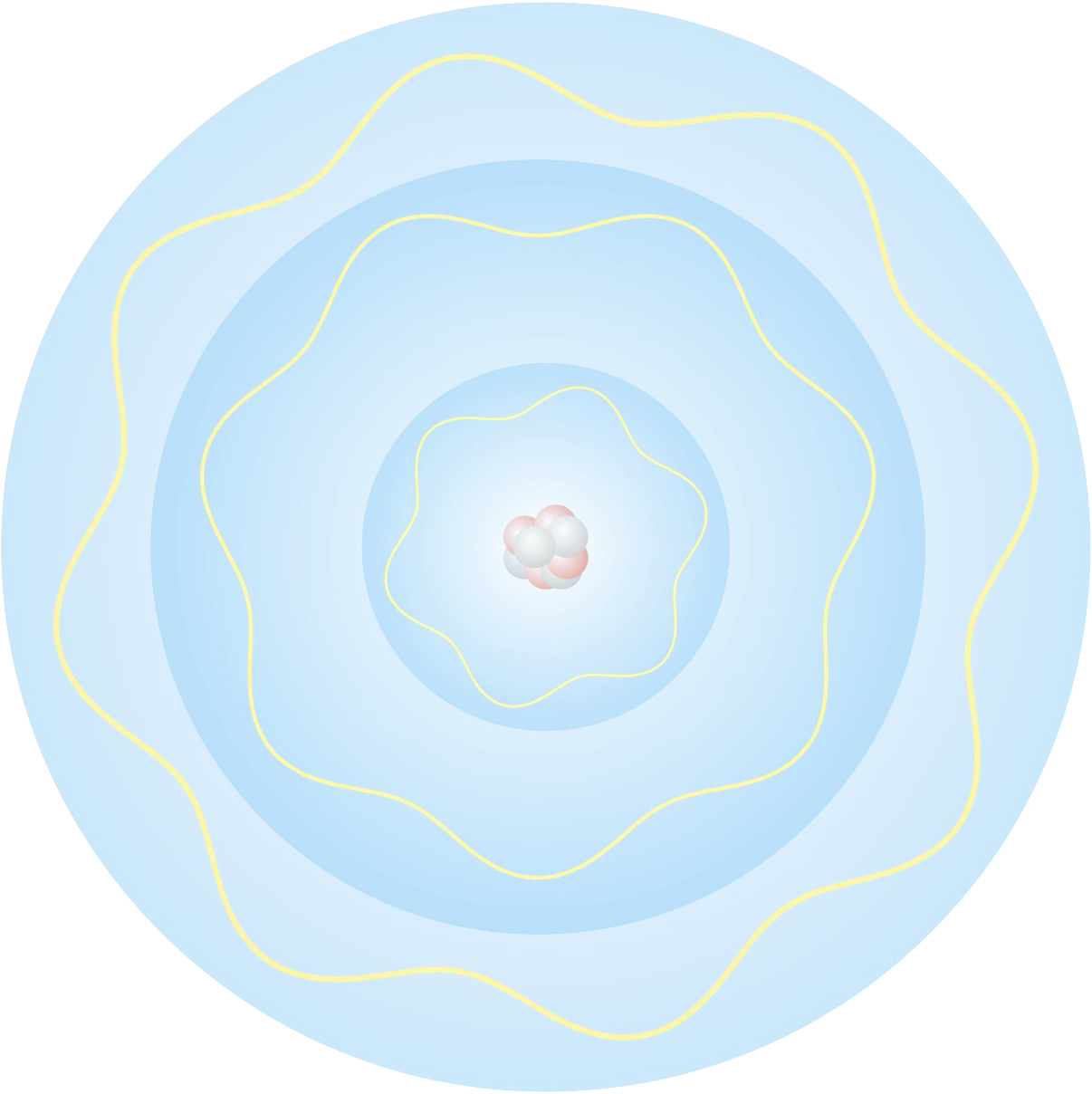
En supposant que la longueur d’onde reste la même sur l’orbite, on doit avoir : $n=\oint\frac{\mathrm{d}\ell}{\lambda}=\oint\frac{p}{h}\mathrm{d}\ell$ (où $n$ est un entier, plus rien à voir avec l’indice optique). Et en supposant une orbite circulaire de rayon $r$, on obtient un moment cinétique $L$ valant : $L=mvr=\frac{nh}{2\pi}=n\hbar$, ce qui est exactement la relation ad hoc introduite par Bohr.

Il ne restait plus qu’à faire le même pas pour la mécanique qu’entre Huygens et Fresnel pour l’optique. Ou comme le dit de Broglie :

La nouvelle dynamique du point matériel (incluant le photon d’Einstein) est à l’ancienne (dynamique classique) ce que l’optique ondulatoire est à l’optique géométrique.

Schrödinger

C’est Schrödinger qui franchira le cap et il va suivre pour cela les pas d’Hamilton.

L’équation de Hamilton-Jacobi peut s’écrire $\frac{\partial S}{\partial t}+H(q, \nabla S)=0$ en notant $\nabla S = \frac{\partial S}{\partial q}$.

Pour une particule libre, $H=p^2 / 2 m$ et on obtient : $\frac{\partial S}{\partial t}+\frac{1}{2 m}|\nabla S|^2=0$ (car $\frac{\partial S}{\partial q}$ vaut aussi l’impulsion $p$).

L’idée-clé de Schrödinger est de remplacer dans l’équation de Helmholtz $\nabla^2 \Psi+k_0^2 n^2 \Psi=0$ l’indice optique $n$ par une fonction liée à l’énergie potentielle $V(q)$ pour trouver l’équation qui régit la « phase » d’une onde mécanique. Pour cela, il va s’aider du travail d’Hamilton sur l’éikonale.

Rappelons-nous qu’en optique géométrique, on obtient l’équation éikonale $|\nabla S|^2=n^2(\mathbf{r})$ en approximant aux petites longueurs d’onde l’équation de Helmholtz pour une solution scalaire $\Psi \propto e^{i k_0 S}$. En faisant la même chose avec une onde mécanique de phase $S_0(q)$, Schrödinger va trouver l’équivalent de l’indice optique.

Équation stationnaire :
Cherchons une fonction d’onde $\Psi(q)$ de la forme $\Psi(q)=A(q) \mathrm{e}^{i S_0(q) / \hbar}$ où $S_0$ est l’action réduite liée à l’énergie $E$ du système par $H(q, \nabla S_0)=E $.
En substituant dans Helmoltz, on impose une relation du type $\nabla^2 \Psi+K(q) \Psi=0$ et on identifie $K(q)$ pour que la limite $\hbar\rightarrow 0$ redonne le bon $|\nabla S|^2$.

Pour une particule soumise à un potentiel $V(q)$, on obtient l’équation stationnaire :
$$\color{#D41876}-\frac{\hbar^2}{2 m} \nabla^2 \Psi(q)+V(q) \Psi(q)=E \Psi(q)$$

Cette équation est l’analogue directe de l’équation de Helmholtz pour la lumière, où $E-V$ joue le rôle de $k^2$.

Équation dépendant du temps :
Schrödinger remarque que pour décrire les états non stationnaires, il suffit de remplacer dans l’équation stationnaire $E$ par $\mathrm{i} \hbar \frac{\partial}{\partial t}$. En effet, pour une onde monochromatique classique de pulsation $\omega$, l’amplitude évolue dans le temps comme $\mathrm{e}^{\mathrm{i}\omega t}$. Et avec $E=h\nu=\hbar\omega$, on peut écrire $\Psi(q,t)=\Psi(q)\mathrm{e}^{\frac{\mathrm{i}}{\hbar}E t}$.
En dérivant temporellement cette solution, on obtient : $\frac{\partial}{\partial t} \Psi(q, t)=-\frac{i E}{\hbar} \Psi(q, t) \Longrightarrow E \Psi=i \hbar \frac{\partial \Psi}{\partial t}$.
Par identification, on voit que l’énergie $E$ agit sur la fonction d’onde comme un opérateur dérivée.

On obtient alors l’équation de Schrödinger dépendant du temps :
$$\color{#D41876}\mathrm{i} \hbar \frac{\partial}{\partial t} \Psi(q, t)=\left(-\frac{\hbar^2}{2 m} \nabla^2+V(q)\right) \Psi(q, t)$$

Sur la vidéo précédente, j’ai envoyé un paquet d’onde gaussien à la rencontre d’une marche de potentiel (un petit potentiel uniforme positif règne à droite alors qu’il est nul à gauche).

Et dans cette vidéo, on constate que le blob réfracté s’éloigne de la normale au dioptre comme le ferait un rayon dans un milieu d’indice optique inférieur. On pourrait s’inquiéter que le blob aille moins vite dans ce milieu (alors qu’en optique, un indice plus faible correspond à une vitesse supérieure). Mais non, tout va bien puisque l’“indice optique” de la mécanique est donné par $\sqrt{2m(E-V)}$ (qui n’est autre que $p$) or $E-V$ est plus faible à droite vu que le potentiel y est plus grand.

Feynman

La contribution de Feynman à la physique est à la confluence de cette longue évolution de l’optique et de la mécanique. Le prix Nobel vient en effet récompenser son travail sur l’électrodynamique quantique, théorie décrivant l’interaction entre la matière et le rayonnement, où il a en particulier remis l’action au centre du jeu.

Feynman semble pourtant à contre-courant du lent cheminement des particules vers les ondes. En effet, pour lui, tout est particule, même la lumière. Il écrit ainsi dans QED: The Strange Theory of Light and Matter (une introduction tout public à l’électrodynamique quantique de laquelle j’ai tiré ce texte il y a très longtemps) :

I want to emphasize to you that light comes in this form – particles. It is very important to know light behaves like particles, especially for those of you who have gone to school where you were probably told something about light behaving like waves. I’m going to tell you the way it does behave like particles.

Néanmoins, ses particules ont des propriétés essentiellement ondulatoires. Selon Feynman, lorsqu’une particule emprunte un chemin pour aller d’un point I à un point F, elle emporte avec elle une phase qui oscille tout le long du chemin. Que vaut la phase finale pour un chemin entier ? $\frac{S}{\hbar}$ où l’action $S$ est calculée sur le chemin considéré !

On peut retrouver ce $\frac{S}{\hbar}$ à partir de la formule de la phase de l’optique ondulatoire $kq-\omega t$ et des relations d’Einstein $E=\hbar\omega$ et de de Broglie $p=\hbar k$.
Découpons le chemin en tronçons infinitésimaux : sur un de ces intervalles, la phase $\phi$ varie de $\mathrm{d}\phi=k \mathrm{d}q - \omega\mathrm{d}t$. En utilisant les équivalences avec l’énergie et l’impulsion, la petite variation de phase devient $\mathrm{d}\phi=\frac{1}{\hbar}(p\mathrm{d}q-E\mathrm{d}t)$.
On force ensuite $\mathrm{d}t$ en facteur : $\mathrm{d}\phi=\frac{1}{\hbar} ( p \frac{ \mathrm{d} q }{ \mathrm{d} t } - E ) \mathrm{d}t=\frac{1}{\hbar}(p\dot{q}-E)\mathrm{d}t$. Plus qu’à substituer $E$ par l’hamiltonien $H$ pour retrouver la formule du lagrangien : $\mathrm{d}\phi=\frac{1}{\hbar}\mathcal{L}\mathrm{d}t$.
Et pour obtenir la variation de phase sur l’entièreté du chemin, on somme les petits déphasages de chaque tronçon infinitésimal, ce qui revient à intégrer le lagrangien le long du chemin : $\Delta\phi=\frac{1}{\hbar}\int_\text{chemin}\mathcal{L}\mathrm{d}t$. C’est bien l’action qu’on retrouve ici et la variation de phase sur le chemin s’écrit finalement $\Delta\phi=\frac{1}{\hbar}S_\text{chemin}$.

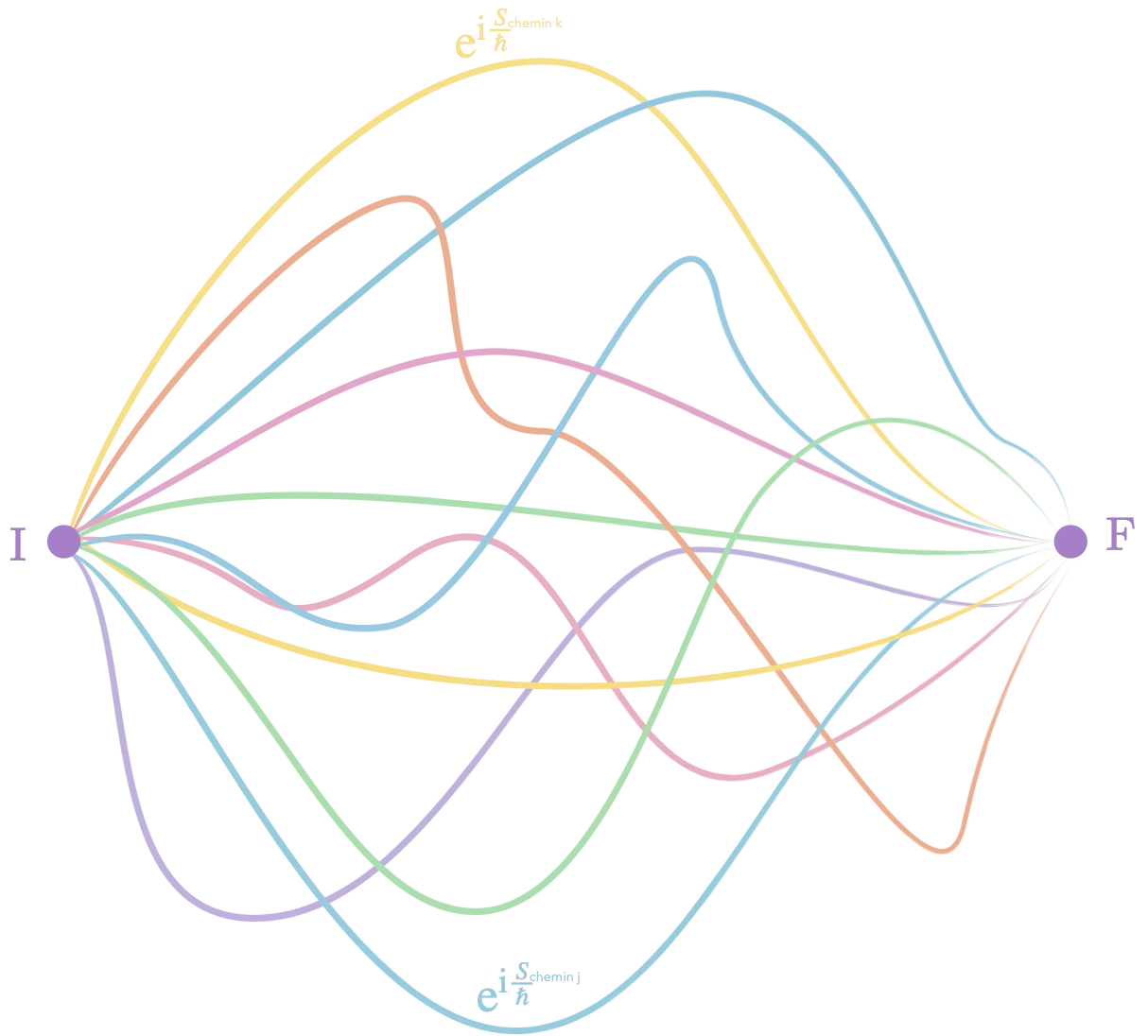
Mais pour Feynman, la particule n’emprunte pas qu’un seul chemin pour aller de I à F, elle emprunte tous les chemins possibles ! Chaque chemin contribue à la probabilité finale de retrouver la particule au point F après être partie du point I.
Pour obtenir la probabilité totale, on se retrouve à additionner entre eux les déphasages obtenus sur chacun des chemins (cela revient à additionner des termes $\mathrm{e}^{\mathrm{i}\frac{S_\text{chemin}}{\hbar}}$). Cela ressemble pas mal au principe de superposition de Huygens-Fresnel…
Feynman aime décrire cette opération comme une somme de petites flèches dans un plan (l’angle de la flèche représente le déphasage). La grande majorité des chemins fournissent des déphasages variant largement les uns par rapport aux autres (la division par $\hbar$ fait gigoter ça très très vite) et sommer des flèches dont l’angle varie quasi aléatoirement ne mène pas très loin… Seuls les chemins où la phase varie très peu de l’un à l’autre vont contribuer efficacement, constructivement, à la somme finale. Or les chemins où la phase varie peu sont les chemins où l’action varie peu. On se retrouve à chercher les trajectoires où l’action est stationnaire redécouvrant le principe de moindre action via le principe de superposition !

Feynman marie ainsi d’une façon nouvelle l’optique ondulatoire à la mécanique en passant directement par la phase et le principe de superposition de Huygens-Fresnel plutôt que par l’équation d’onde d’Helmholtz et met dans le même mouvement l’action au centre de son formalisme.

Bouclons la boucle en reprenant un exemple donné par Feynman dans QED.
On a une source de photons monochromatiques (leur énergie $E$ est donc fixe) et un détecteur. Un écran cache la source au détecteur mais un miroir est placé en dessous.
La probabilité que le détecteur capte un photon doit être calculée en utilisant tous les chemins possibles. Pour simplifier, Feynman découpe le miroir en 13 et ne s’autorise que les trajets rectilignes.

Dans cette situation l’action obtenue sur chaque chemin dépend seulement de la longueur du trajet (en effet, à énergie constante l’action se réduit $\int p\mathrm{d}q$ (action réduite) et pour un photon, $p=\frac{E}{c}$. Donc $E\frac{L}{c}$ ou encore $E\tau$, l’action et donc le déphasage de chaque chemin est proportionnel au temps de parcours.
En sommant sur les chemins, on constate bien que les contributions les plus importantes (car de phases quasi constantes) sont celles proche de la trajectoire la plus courte (on a retrouvé Fermat !).

Sources :

• Mesli, A. « Genèse et développement du principe de moindre action. Première partie : de Fermat (1655) à Lagrange (1756) », Photoniques n° 80, p. 34–40 (janvier 2016).
• Mesli, A. « Genèse et développement du principe de moindre action. Deuxième partie : de Hamilton (1834) à Feynman (1942) », Photoniques n° 81, p. 37–45 (avril 2016). 🌐
• Vaquero Vallina, M. « On the Geometry of the Hamilton–Jacobi Equation », thèse de doctorat, Universidad Autónoma de Madrid – Instituto de Ciencias Matemáticas (ICMAT), soutenue le 27 novembre 2015. 🌐
• Houchmandzadeh, B. “The Hamilton–Jacobi equation: An alternative approach”, American Journal of Physics 88 (5), 353–359 (Mai 2020) 🌐
• Wheeler, N. “Schrödinger’s train of thought”, Reed College Physics Department essay, avril 2006. 🌐
• les portraits sont plus ou moins hallucinés par IA.