Arcs électriques
Le champ disruptif d’un isolant, ou plutôt sa rigidité diélectrique, désigne la valeur de champ électrique maximale que le milieu peut supporter avant le déclenchement d’un arc électrique, ou claquage.
Pour l’air, la valeur fréquemment admise est de $\pu{36 kV/cm}$ dans l’air sec et tombe à $\pu{10 kV/cm}$ pour un air saturé en humidité. Cela signifie qu’il faut, dans l’air sec, une tension d’au moins $\pu{36 kV}$ entre deux électrodes séparées d’un centimètre pour qu’une étincelle se crée entre elles.
Comment retrouver cet ordre de grandeur à partir de considérations physiques simples ?

Un arc électrique est un conduit d’air ionisé, du plasma (le 4e état de la matière). Son origine ?
Un champ électrique suffisamment costaud.
Imaginons qu’un électron soit arraché à une molécule d’air. Il est alors accéléré par le champ électrique ambiant et gagne ainsi de l’énergie cinétique. Si au moment de rencontrer une nouvelle molécule, l’électron a atteint une énergie suffisante pour la ioniser, on peut se retrouver avec une cascade d’ionisations successives !
Le secret est donc d’avoir un champ suffisant pour donner à un électron une énergie cinétique de l’ordre de grandeur de l’énergie de ionisation d’une molécule (autour de la dizaine d’électronvolts) sur une distance correspondant à son libre parcours moyen dans l’air.
Faisons le point sur le libre parcours moyen dans un gaz de particules identiques de rayon $d$ et de densité $n$ :
La section efficace de collision $\sigma$ vaut $\pi d^2$.

$$ \begin{aligned} v_{rel}&=\sqrt{\vec{v}_{rel}\cdot \vec{v}_{rel}}\\ &=\sqrt{\left(\vec{v}_2-\vec{v}_1\right)\cdot\left(\vec{v}_2-\vec{v}_1\right)}\\ &=\sqrt{\vec{v}_2\cdot\vec{v}_2+\vec{v}_1\cdot\vec{v}_1-2\vec{v}_2\cdot\vec{v}_1} \end{aligned} $$
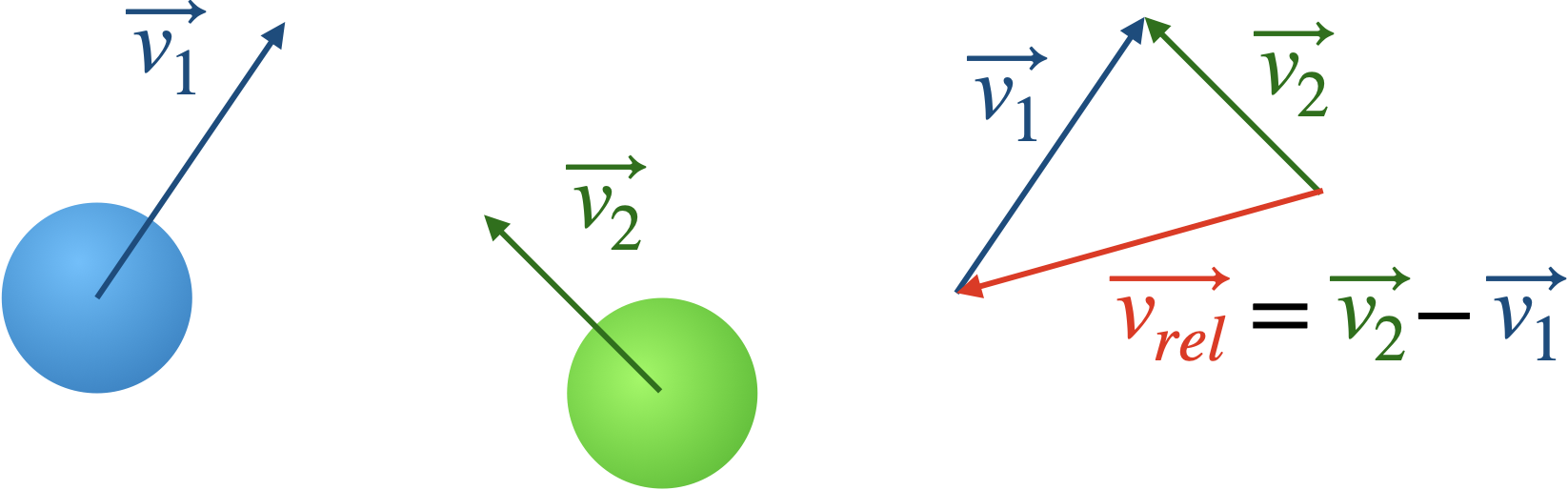
Pour obtenir la vitesse relative moyenne, on va supposer que les vitesses des particules se répartissent aléatoirement selon une certaine distribution de probabilité.
$$ \begin{aligned} \overline{v_{rel}}&=\sqrt{\overline{\vec{v}_2\cdot\vec{v}_2}+\overline{\vec{v}_1\cdot\vec{v}_1}-2\,{\cancel{\overline{\vec{v}_2\cdot\vec{v}_1}}}}\\ &= \sqrt{\overline{\vec{v}_2^2}+\overline{\vec{v}_1^2}}\\ &= \sqrt{2}\overline{v} \end{aligned} $$
On suppose en effet que les vitesses des particules 1 et 2 ne sont pas corrélées (${\vec{v}_2\cdot\vec{v}_1}=0$) et que leurs valeurs moyennes sont les mêmes ($\overline{\vec{v}_2^2}=\overline{\vec{v}_2^2}=\overline{v}^2$).
Le nombre de collisions d’une particule pendant un laps de temps $\Delta t$ peut être estimé comme le nombre moyen de fois que le centre de masse d’une particule se trouve dans le volume balayé par la section efficace $\sigma$ pendant $\Delta t$, c’est-à-dire sur une distance $\overline{v_{rel}}\Delta t$.
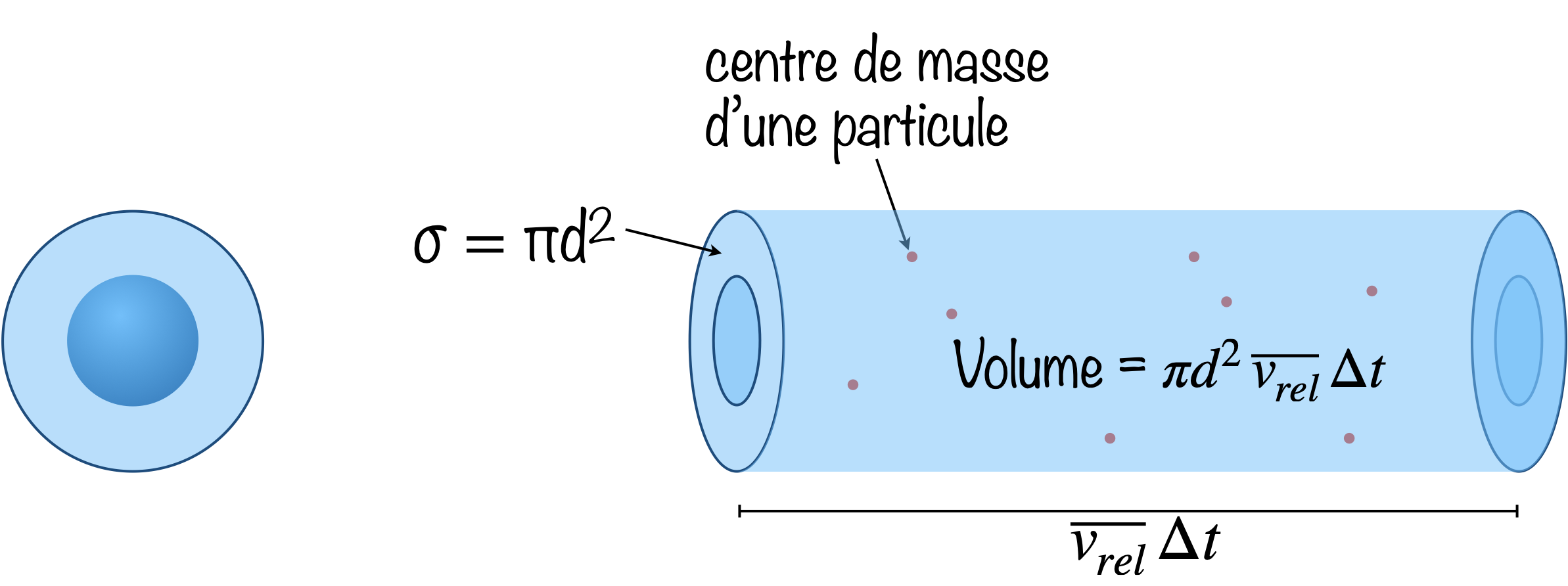
Le volume en question vaut $V=\sigma \,\overline{v_{rel}}\,\Delta t$.
Et le nombre de particules rencontrées vaut donc $nV=n\,\sigma\, \overline{v_{rel}}\,\Delta t= \sqrt{2}\,n\,\sigma\, \overline{v}\,\Delta t= \sqrt{2} \,n\,\pi \,d^2 \,\overline{v}\,\Delta t$.
Le libre parcours moyen $\lambda$ va alors correspondre à la distance parcourue pendant $\Delta t$ divisée par le nombre de collisions ayant eu lieu pendant ce laps de temps.
D’où :
$$ \begin{aligned} \lambda &= \frac{\cancel{\overline{v}\Delta t}}{\sqrt{2}n\sigma {\cancel{\overline{v}\Delta t}}}\\ &=\frac{1}{\sqrt{2}n\sigma}\\ &=\frac{1}{\sqrt{2}n\pi d^2} \end{aligned} $$
Le libre parcours moyen ne dépend donc que de la taille des particules et de leur densité, pas de leur vitesse relative !
Pour un gaz à pression $P$ et température $T$, on peut utiliser en première approximation la relation des gaz parfaits pour obtenir la densité de particules :
$n=P/k_B T$.
En remplaçant dans $\lambda$, on obtient :
$$ \lambda = \frac{k_B T}{\sqrt{2}P\pi d^2} $$
Une molécule de diazote a un diamètre $d=\pu{0,37 nm}$ et pour une pression $P=\pu{1 bar}$ et une température $T = \pu{293 K}$, on obtient un libre parcours moyen $\lambda\approx \pu{66 nm}$.
On peut remarquer que c’est près de 200 fois plus grand que la distance moyenne entre particules donnée par $1/n^{\frac{1}{3}}=\left(\frac{k_B T}{P}\right)^{\frac{1}{3}}\approx \pu{3,4 nm}$ !
Pour vérifier, on simule un gaz idéal dans un cube de 100 nm de côté avec des conditions aux limites périodiques contenant environ 24 000 molécules considérées comme des sphères dures de diamètre 0,37 nm et dont la vitesse est tirée dans la distribution de Maxwell-Boltzmann pour une température de 300 K. On suit la trajectoire d’une molécule particulière tracée en rouge. Après 30 collisions, la moyenne des libres parcours est de 68 nm.
Pour un électron, on peut reprendre la formule du libre parcours moyen en modifiant seulement un peu la section efficace puisque $\sigma=\pi\left(r_\text{molécule}+r_\text{électron}\right)^2\approx \pi \left(r_\text{molécule}\right)^2 = \pi d^2 /4$.
Et donc $\lambda= \frac{2\sqrt{2}k_B T}{P\pi d^2}\approx 0,27 \text{ μm}$.
Notre électron devant récupérer une énergie d’environ $\pu{20 eV}$ sur la distance $\lambda$ pour réussir à ioniser la prochaine molécule de diazote rencontrée, le champ doit donc être de $\pu{20 V}/\lambda$, soit à peu près $\pu{20 V}$ pour $0,27 \text{ μm}$ $\rightarrow$ $0,74\text{ MV/cm.}$ C’est plus d’un ordre de grandeur au-dessus de ce qu’on aurait aimé obtenir 😢.
Une des raisons possibles de cet écart est notre trop grand optimisme quant à l’efficacité des collisions ; il est en effet fort peu probable qu’un électron parvienne à ioniser systématiquement chaque molécule qu’il rencontre, en particulier avec une énergie à peine suffisante.
Cela revient au final à surestimer la section efficace de collision. Penchons-nous alors sur la littérature pour trouver une valeur plus réaliste…
Le graphique suivant rapporte un tas de sections efficaces différentes pour des collisions électron-diazote donnant lieu à des rotations, des vibrations, ou (et c’est ce qui nous intéresse ici) des ionisations :
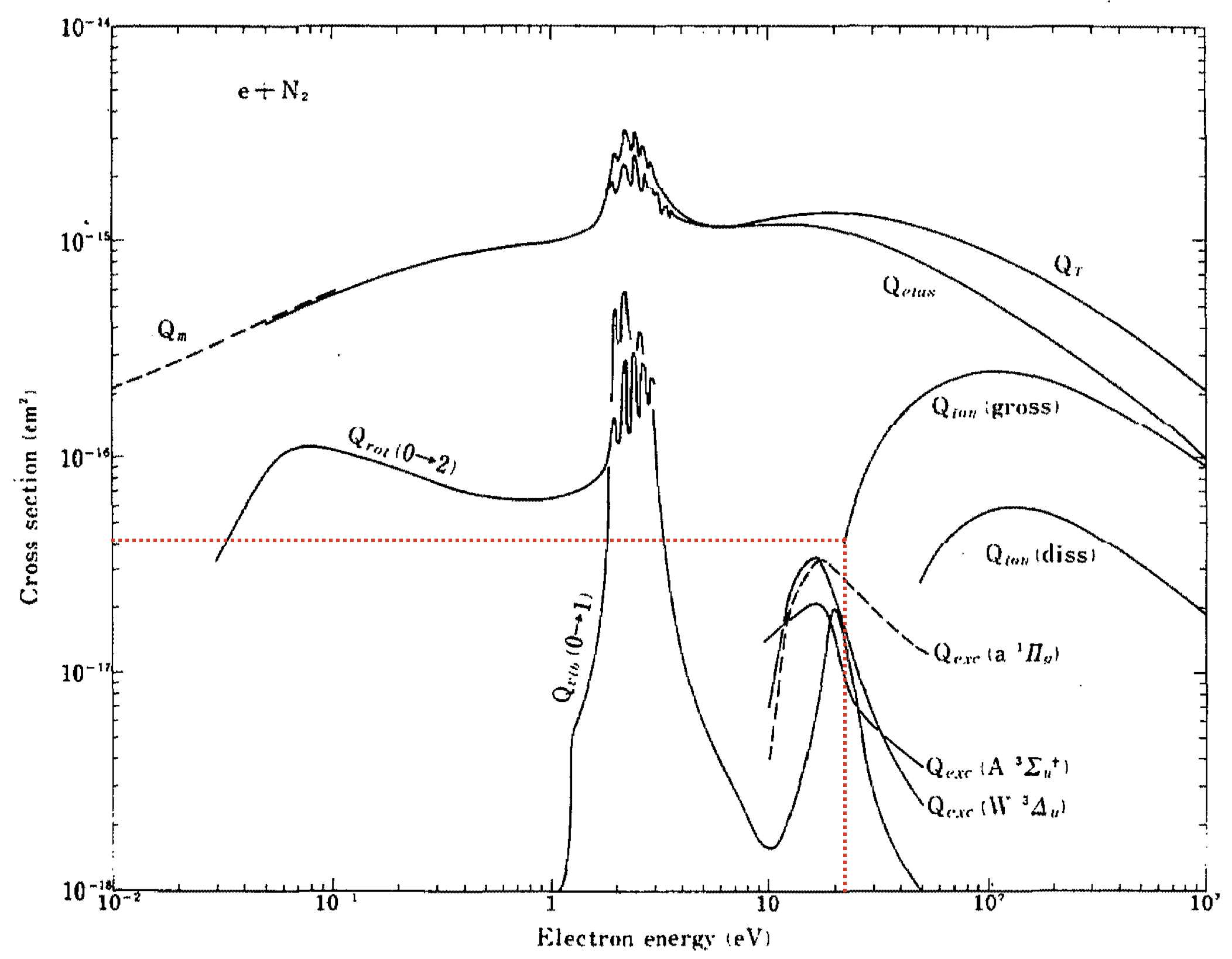
Y. Itikawa et al. Cross Sections for Collisions of Electrons and Photons with Nitrogen Molecules, Journal of Physical and Chemical Reference Data 15, 985 (1986)
D’après le graphique, l’énergie minimale que doit atteindre l’électron pour obtenir la ionisation du diazote semble être un peu supérieure à $\pu{20 eV}$, et la section efficace associée vaut approximativement $\pu{4e-17 cm2}$.
Cela nous donne un libre parcours moyen de $\frac{1}{\sqrt{2}n\sigma}=7\text{ μm}$, largement supérieur à notre prédiction initiale !
Le champ électrique correspondant vaut, roulement de tambour… $20\text{ eV}/7 \text{ μm}\approx\pu{30 kV/cm}$. Youpi !