Analyse en composantes principales

Les axes qui tiraillent territorialement la France

Détaillons un exemple sur le modèle de celui des prénoms dans la vidéo.

L’idée ici est de récupérer plein de séries de données départementales disparates sur le site de l’INSEE pour voir si les composantes principales font ou non ressurgir une géographie identifiable de ce brouillard de chiffres. On peut alors s’amuser à balbutier des interprétations pour ces axes de différentiation territoriaux et probablement irriter ainsi fortement tout sociologue un tant soit peu éduqué. C’est la magie même de l’ACP de permettre à un quidam de se prendre pour un sociologue…

Cherchant à étudier la variabilité entre départements, à faire ressortir leurs spécificités, on choisit ici de n’avoir que des données sous forme de taux quitte à rendre relative certaines données brutes en divisant par la population du département. Certes, un vecteur associant les variables non relatives aurait probablement constitué la 1^re composante principale puisque la démographie explique alors une large part de la variance, et comme chaque composante est orthogonale aux suivantes, cela aurait peut-être éliminé ce biais dès la 2^e composante… Mais autant s’en débarrasser dans les données pour éviter toute confusion.

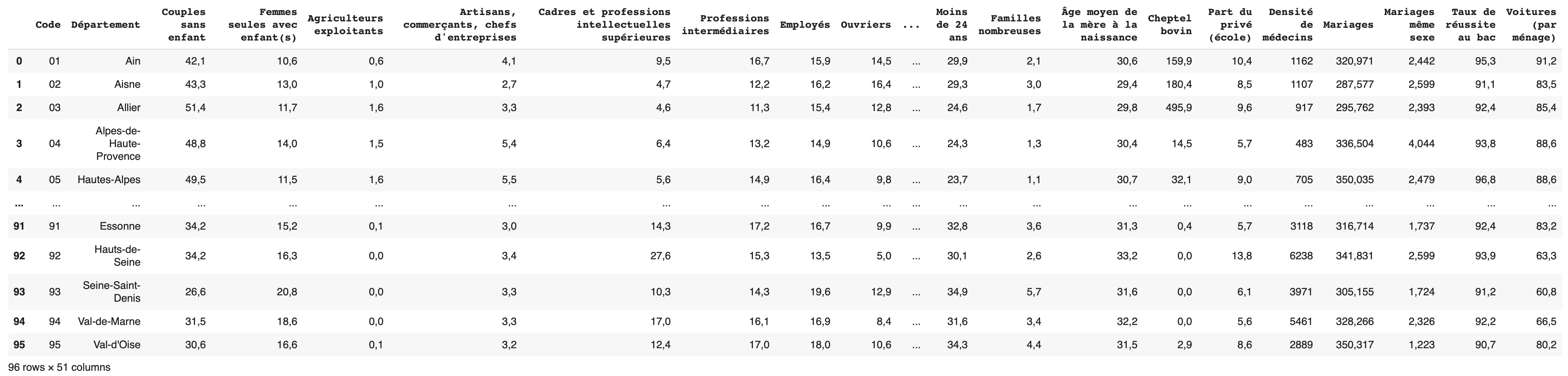
Un tableau de 96 lignes (les départements métropolitains) et 51 colonnes (code du département + nom du département + 49 variables statistiques) constitue les données de base. Un export en .csv (accès au fichier) et direction Pandas.

import pandas as pd
file_path = "tableauINSEE.csv"
data = pd.read_csv(file_path, delimiter=';')

On nettoie un peu en changeant les virgules françaises en points américains comme séparateurs décimaux afin que Pandas daigne associer des nombres (des flottants) aux données.

departements = data.columns[2:]
data_cleaned = data[columns_to_use].replace(',', '.', regex=True).apply(pd.to_numeric, errors='coerce')

Puis on standardise les vecteurs : pour chaque série de 96 valeurs (les valeurs départementales de chaque catégorie statistique), on centre les données en soustrayant la moyenne et on les met à l’échelle en divisant par l’écart type, de sorte que les coordonnées des vecteurs aient tous une moyenne de 0 et un écart type de 1.

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
data_normalized = scaler.fit_transform(data_cleaned)
data_normalized_df = pd.DataFrame(data_normalized, columns= departements)

Voilà par exemple la carte de la variable “cheptel bovin”. Une carte = un vecteur à 96 dimensions.

Traçons la matrice de corrélation de ces 49 variables pour faire connaissance.

import plotly.express as px

# Calculer la matrice de corrélation
correlation_matrix = data_normalized_df.corr()

# Créer un heatmap de la matrice de corrélation
fig = px.imshow(
    correlation_matrix,
    labels=dict(x="Variables", y="Variables", color="Corrélation"),
    x=correlation_matrix.columns,
    y=correlation_matrix.columns,
    color_continuous_scale='Temps'
)

Enfin, on applique l’analyse en composantes principales sur les vecteurs normalisés.

Rq : les fonctions utilisées pour la normalisation et l’ACP viennent de différents modules de la bibliothèque Scikit-learn spécialisée dans le machine learning.

from sklearn.decomposition import PCA

pca = PCA()
pca_components = pca.fit_transform(data_normalized)
pca_df = pd.DataFrame(pca_components, columns=[f'Composante {i+1}' for i in range(pca_components.shape[1])])

Traçons le “scree plot” qui représente le pourcentage de variance expliquée en fonction des composantes.

import numpy as np
import plotly.graph_objs as go

# Récupérer la variance expliquée pour les 20 premières composantes principales
explained_variance = pca.explained_variance_ratio_[:20]

# Calculer la variance expliquée cumulée
explained_variance_cumulative = np.cumsum(explained_variance)

# Création du scree plot
fig = go.Figure()

# Ajouter les barres pour la variance expliquée individuelle
fig.add_trace(go.Bar(
    x=[f'Composante {i+1}' for i in range(len(explained_variance))],
    y=explained_variance,
    name='Variance expliquée individuelle',
    marker=dict(color='rgba(55, 128, 191, 0.7)'),
))

# Ajouter la ligne pour la variance expliquée cumulée
fig.add_trace(go.Scatter(
    x=[f'Composante {i+1}' for i in range(len(explained_variance))],
    y=explained_variance_cumulative,
    name='Variance expliquée cumulée',
    mode='lines+markers',
    line=dict(color='rgb(255, 0, 0)'),
))

# Mise en page du graphique
fig.update_layout(
    title='Scree Plot',
    xaxis_title='Nombre de composantes principales',
    yaxis_title='Pourcentage de variance expliquée',
    showlegend=True,
    template='plotly_white'
)

# Afficher le graphique
fig.show()

On constate que la 1^re composante explique presque 40% de la variance et qu’arrivé à la 6^e, on dépasse 80% d’explication.

Affichons les valeurs de la première composante sur une carte de France. Les départements scorant positivement fort sur cette composante apparaisse jaune et ceux scorant le plus négativement sont en bleu.

# Ajouter les codes départements et leurs noms à la dataframe des composantes principales
pca_df['Code'] = data['Code']
pca_df['Département'] = data['Département']

# Choisissez la composante à afficher
composante = 'Composante 1'

# Créer la carte
fig = px.choropleth_mapbox(
    pca_df,
    geojson="https://france-geojson.gregoiredavid.fr/repo/departements.geojson",  # GeoJSON pour les départements français
    locations='Code',
    featureidkey="properties.code",
    color=composante,
    color_continuous_scale="Viridis",
    mapbox_style="white-bg",  # Fond de carte blanc
    zoom=5,
    center={"lat": 46.603354, "lon": 1.888334},  # Centre de la France
    opacity=1,
    labels={composante: composante},
    hover_name='Département',  # Afficher le nom du département
    hover_data={'Code': False, composante: True},  # Supprimer le code du département et afficher la composante
)

fig.show()

Cette composante semble opposer les départements dont la population vit pour une large part en ville aux départements plus ruraux.

Dévoilons la recette de cette 1^re composante en détaillant les proportions dans lesquelles interviennent chaque ingrédient (les variables statistiques). Pour cela, on trace l’histogramme des différentes charges (ou loadings) triées. Les coefficients de charges correspondent aux poids respectifs de chaque variable dans le vecteur.

numero_composante = 1
composante = f'Composante {numero_composante}'

# Récupérer les loadings pour la composante choisie
loadings_composante = loadings[composante]

# Trier les loadings par valeur décroissante
loadings_composante_sorted = loadings_composante.sort_values(ascending=False)

# Créer un DataFrame pour Plotly Express
loadings_df = pd.DataFrame({
    'Variable': loadings_composante_sorted.index,
    'Loading': loadings_composante_sorted.values
})

# Créer un histogramme des loadings avec une coloration en fonction des valeurs
fig = px.bar(
    loadings_df,
    x='Variable',
    y='Loading',
    color='Loading',  # Utilisation des valeurs pour la coloration
    color_continuous_scale='Viridis',  # Choix de l'échelle de couleurs
    template='plotly_white',
    title=f'Loadings triés pour la {composante}',
    height=600,
)

# Supprimer la colorbar si vous ne souhaitez pas l'afficher
fig.update_coloraxes(showscale=False)

# Afficher le graphique
fig.show()

Les marqueurs de l’urbanité sont bien opposés à ceux de la ruralité.
Les différences de mode de vie entre ces environnements semblent donc responsables du plus gros de la distinction entre départements (du moins pour le lot de variables choisis qui sont malgré tout très disparates).

On peut renforcer cette interprétation en vérifiant comment une nouvelle variable, la “part de la population vivant dans une unité urbaine en 2017” score sur un plan formé par les deux premières composantes.

La variable “population urbaine” représentée par un segment rouge a comme prévu une direction proche de la composante 1 et lui est donc fortement corrélée (on a aussi placé les départements dans ce plan en les coloriant en fonction de leur valeur de la variable population urbaine).

Une fois cette opposition ville-campagne retirée, que reste-t-il pour expliquer les 60% de variance résiduelle entre départements ?

D’après la deuxième composante, l’axe sur lequel les valeurs des départements s’étalent le plus semble correspondre à une dimension socio-économique. Cela semble montrer que la répartition des richesses sur le territoire est loin d’être homogène à l’échelle des départements ; certains concentrent les marqueurs de richesse et d’autres accumulent les stigmates de la pauvreté.

La troisième composante matérialise une opposition géographique entre le Nord et le Sud (avec Paris dans le camp du Sud) grâce à un axe allant des ouvriers aux artisans/commerçants.

La quatrième composante distingue principalement positivement Paris avec de forts taux de fonctionnaires, de médecins et de mariages de même sexe, et des petits taux de voitures par ménage et d’employés. Le contraste est maximale avec la Corse, le nord des Alpes et la grande couronne.

La cinquième composante semble très politique avec un axe allant de Mélenchon-Lassalle à Zemmour-Le Pen. Le vote protestataire semble ainsi se polariser territorialement. L’urbanité de la Seine-Saint-Denis en soutien de Mélenchon allié au Sud-Ouest rural de Lassalle contre un vote d’extrême-droite plus à l’Est.

Paris score bizarrement très fort négativement bien que le vote pour l’extrême droite y soit plus rare qu’ailleurs.

Détaillons les valeurs pour chaque catégorie statistique normalisée à Paris (on a conservé l’ordre des charges de la composante 5).

Voilà ce que deviennent ces valeurs après multiplication par les charges de la composante 5.

Et en sommant toutes ces valeurs, on obtient la projection de Paris et la composante 5. Le résultat d’environ -3,8 est bien celui attribuée à Paris dans la carte de la composante. On voit ainsi que les variables politiques ne sont pas celles qui participent au score de Paris.

La sixième composante oppose bizarrement le vote Pécresse aux mariages… Et fait ressortir géographiquement le centre par rapport aux bords.

En comparant la carte du vote Pécresse à celle du taux de mariage, on observe bien une très légère complémentarité mais cela n’a rien de concluant et c’est confirmé par la corrélation de -0,063 entre les deux variables. On ne peut pas vraiment se contenter des extrémités de l’axe pour tenter une interprétation.

L’attelage leader de cette composante est pour le moins curieux : les Hauts-de-Seine et la Creuse ! Mais les variables qui tirent leurs scores sont en bonne partie différentes. Un vote Pécresse en 2022 relativement plus fort qu’ailleurs semble d’ailleurs le seul vrai point commun.

Le semblant d’homogénéité géographique avec un centre qui s’oppose aux bords laisse cependant supposer que quelque chose se trame dans cette composante et on peut hasarder quelques hypothèses sociologiques de bistrot. La composante semble agglomérer une France rurale âgée au tissu sociale distendue (plus de morts, moins de mariages) votant plus qu’ailleurs pour la droite historique. Et elle lui adjoint deux départements (Hauts-de-Seine et Yvelines) abritant une haute bourgeoisie plus dense qu’ailleurs ayant pour seul point commun notable de voter pour cette même droite.

La septième composante a pour pôles la proportion d’écoles privées d’un côté et les mariages de même sexe de l’autre. L’opposition est amusante mais le reste du vecteur ne semble pas vouloir se prêter à des interprétations faciles pas plus que la répartition géographique (au-delà de la zone bretonne au sens large ou le privé est surreprésenté).

À la louche ou plutôt au godet d’une pelleteuse, on a donc les axes de séparation territoriaux suivant (à l’échelle des départements), par ordre de pertinence :

Ville contre campagne
Riches contre pauvres
Ouvriers contre artisans/commerçants
Paris contre le reste
Vote radical de gauche et protestataire rural contre vote d’extrême droite
Droite historique contre le reste
Religieux contre mariage pour tous