Curse of dimensionality
L’expression Curse of dimensionality (Fléau de la dimension dans sa traduction française) vient de l’américain Richard Bellman alors qu’il considérait des problèmes en programmation dynamique (qu’il inventa en 1953).
Mais qu’est-ce donc que ce “fléau” ?
Le volume d’un cube de côté $a$ dans un espace à $n$ dimensions vaut $a^n$. Jusque là, ça va.
Pour la boule, de rayon $R$, c’est plus compliqué…
- à 1D, la boule se réduit à un segment de longueur $R$.
- à 2D, c’est un disque de “volume” $\pi R^2$. Ce qu’on appelle aire dans notre monde 3D est bien le volume (l’espace contenu à l’intérieur) d’un monde 2D.
- à 3D, le volume de la boule vaut $\frac{4}{3}\pi R^3$.
Pour des boules de rayon 1, ça nous donne les volumes suivant : $1$ à 1D, $\pi$ à 2D, $\frac{4\pi}{3}$ à 3D. Est-ce que cela continue d’augmenter pour les dimensions supérieures ?
Aussi bizarre que cela puisse paraître, on va voir que le volume culmine en dimension 5 puis s’effondre jusqu’à presque s’évanouir !
La petite énigme suivante va nous familiariser avec ces bizarreries.
Petite énigme
On prend un $n$-cube (cube de dimension $n$) de côté $4$ et on y place à l’intérieur autant de $n$-boules de rayon $1$ que l’on peut.
Quel sera le rayon de la plus grande $n$-boule possible que l’on pourra placer au centre de la boite, dans l’espace laissé libre par les autres boules ?
On peut décomposer la boite en $2^n$ sous-boites de côté $2$ contenant chacune une boule de côté $1$.
- à 1D, il ne reste aucune place pour une sphère au milieu : le $1$-cube de côté $4$ est un segment de longueur $4$ dans lequel on peut placer deux $1$-boules de rayon $1$ qui sont des segments de longueur $2$.
- à 2D, 4 $2$-boules (disques) sont placés dans le $2$-cube (carré). Pythagore nous dit que la distance entre le centre de chaque boule et le centre de la boite vaut $\sqrt{R^2+R^2}=R\sqrt{2}$. Par conséquent, le rayon de la plus grande $2$-boule (disque) que l’on peut placer au centre est de $R\sqrt{2}-R\Rightarrow\sqrt{2}-1$.
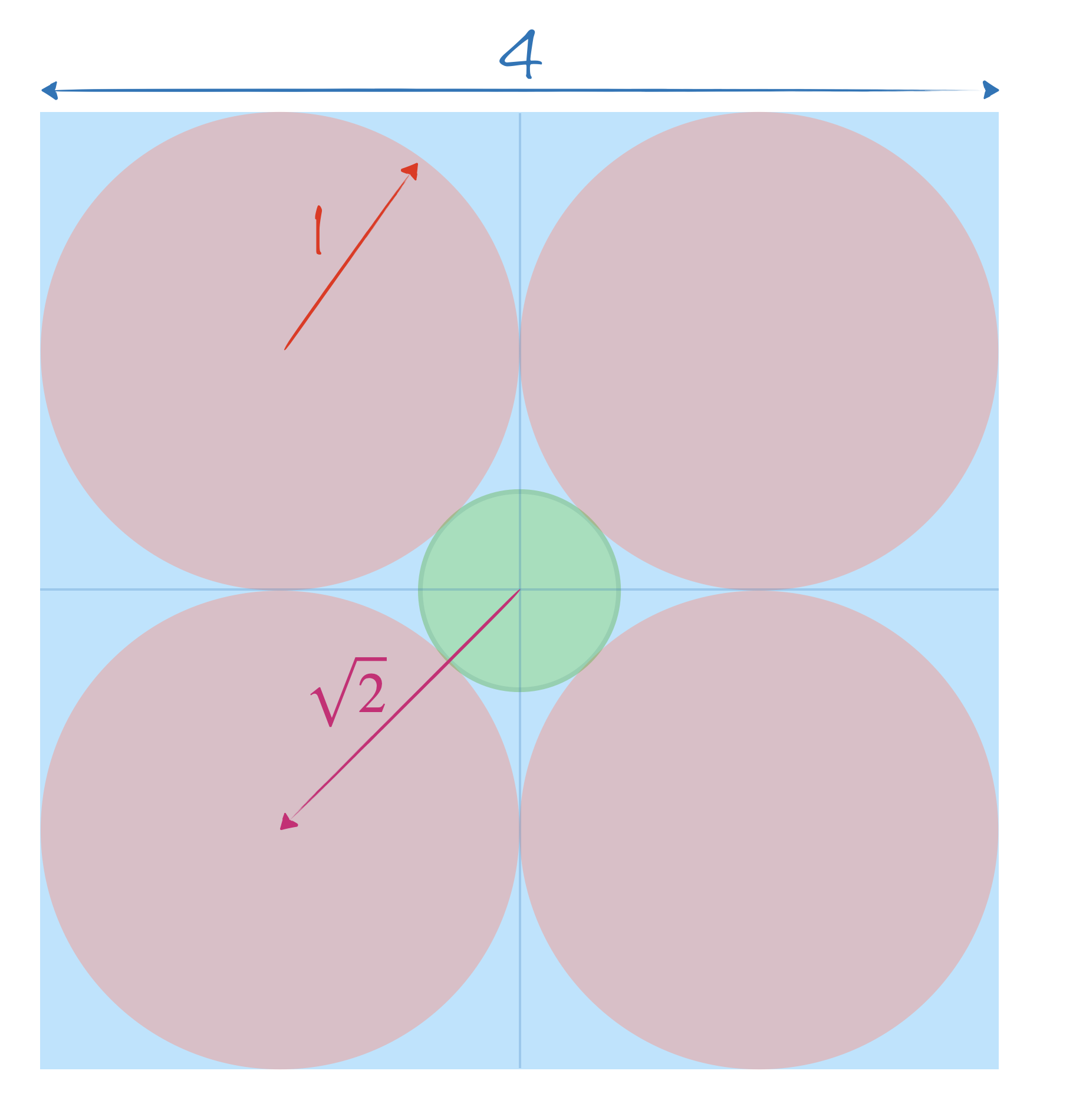
- à 3D, on place 8 $3$-boules dans le $3$-cube. On peut faire le même raisonnement qu’à 2D pour trouver la distance entre le centre des $3$-boules et celui de la boite. C’est toujours Pythagore qui nous aide (du moins sa généralisation à $n$ dimensions) et on obtient comme plus grand rayon possible pour la $3$-boule du milieu : $\sqrt{R^2+R^2+R^2}-R = R\sqrt{3}-R \Rightarrow \sqrt{3}-1$.
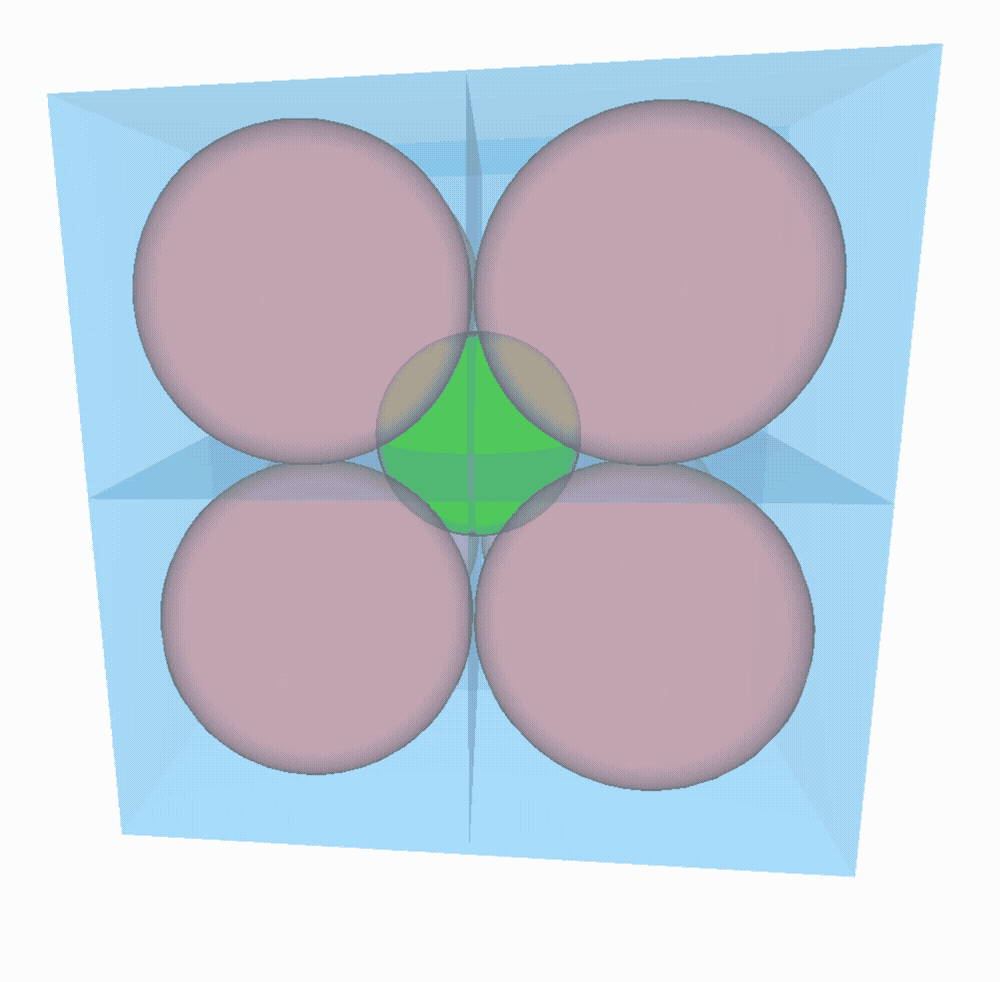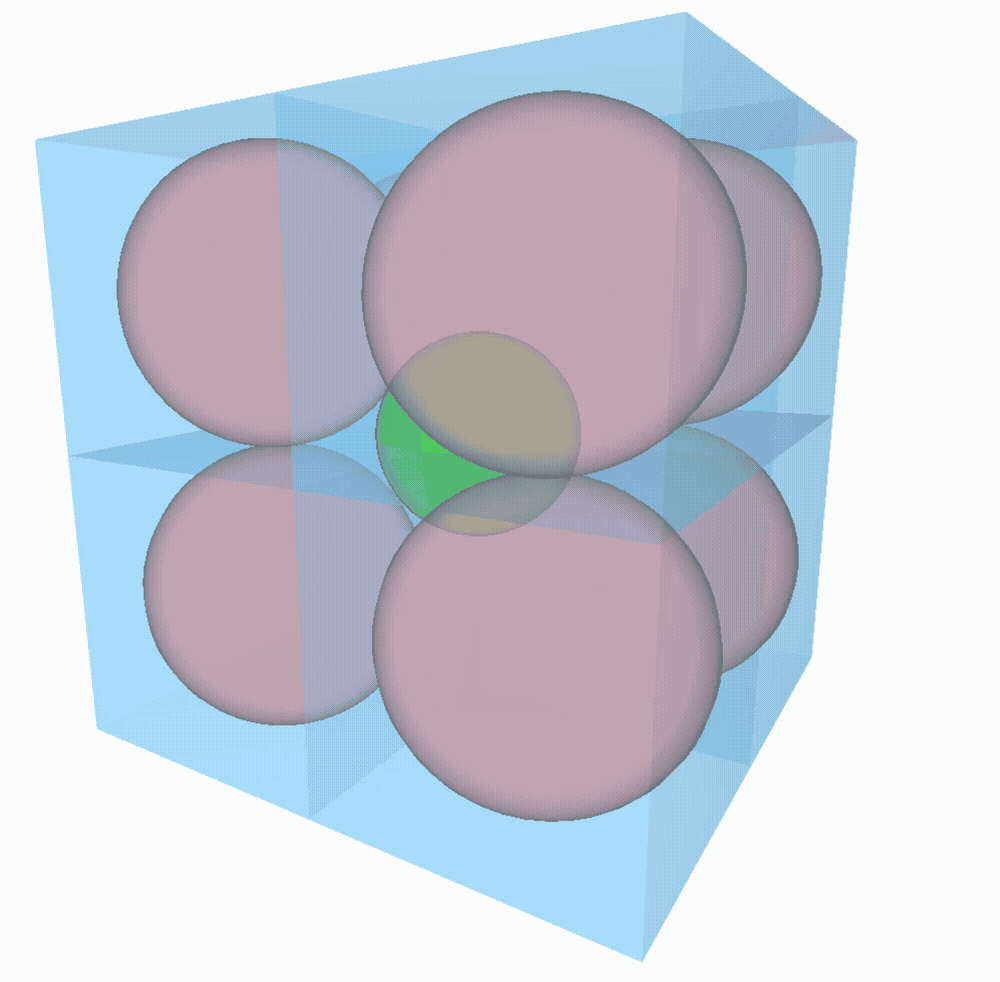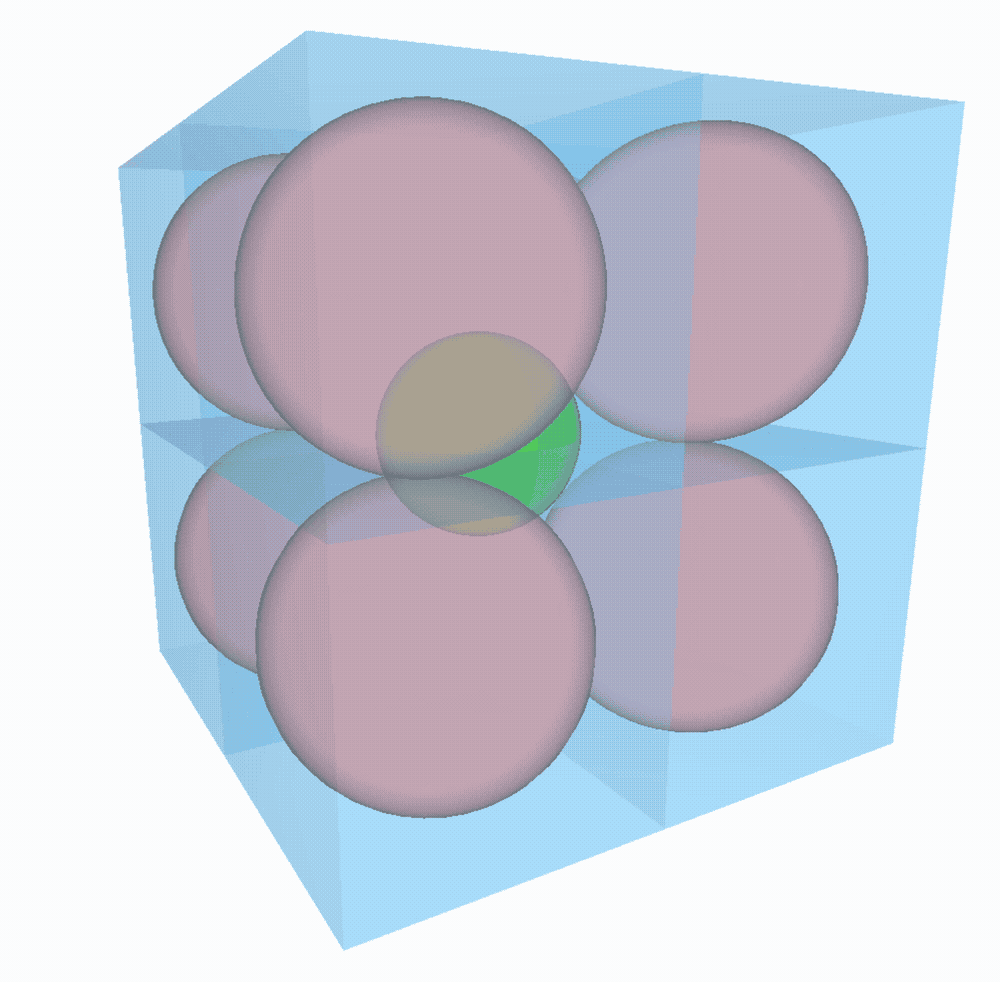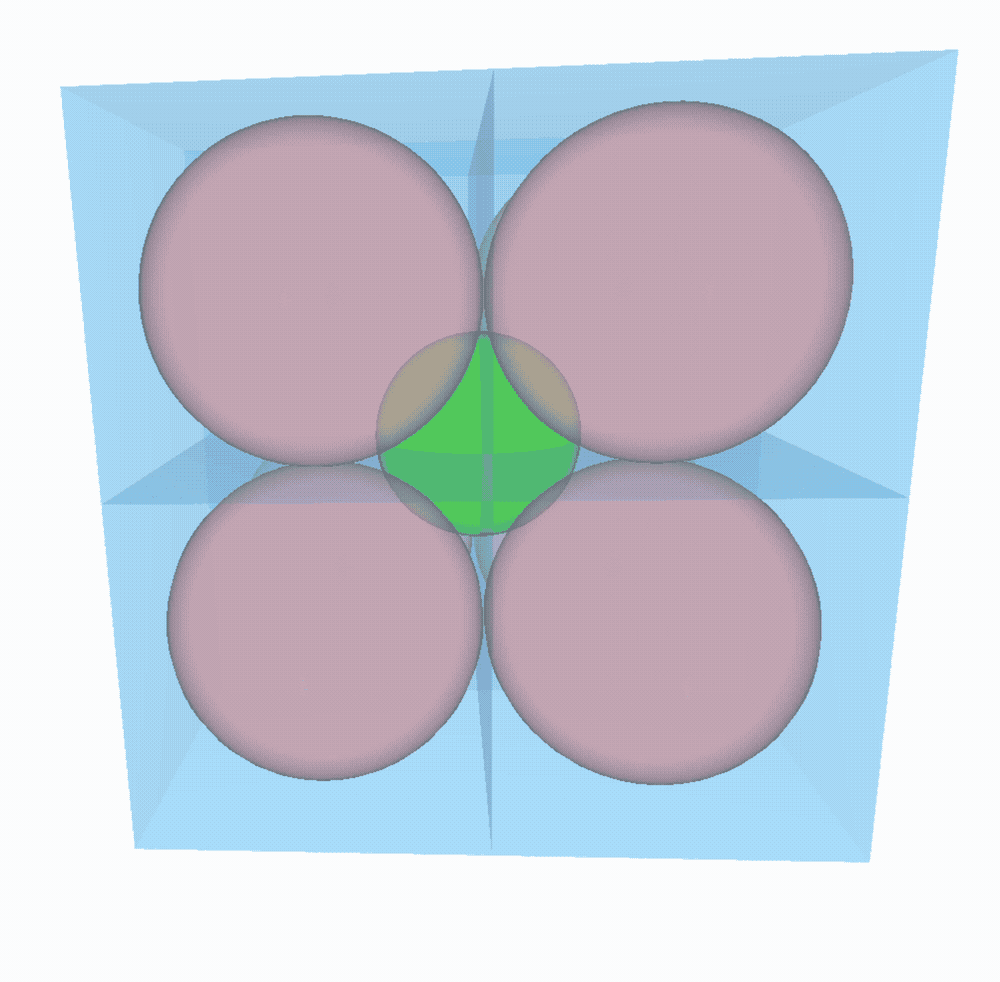
On peut sans problème généraliser à $n$ dimensions. Le rayon de la sphère du milieu vaudra $\sqrt{n}-1$. Facile !
Mais regardons maintenant ce que cela signifie.
À 4D, la sphère du milieu est aussi grande que les 16 autres ! À 9D, le rayon de la sphère centrale vaut 2 !!! Elle est deux fois plus grande que les 512 voisines et elle touche les parois de la boite. À partir de 10D, la boule centrale déborderait de la boite… Sorcellerie !
Volume d’une $n$-boule
Le volume $V_n$ d’une $n$-boule de rayon $R$ peut se déterminer grâce à la formule de récurrence suivante $\displaystyle V_n(R)=\frac{2\pi R^2}{n} V_{n-2}(R)$
En prenant $V_0(R) =1$ (à partir de la formule du cube $a^n$) et $V_1(R)=2R$, on peut déterminer le volume en toute dimension.
Démonstration de la formule de récurrence :
Le volume du $n$-boule est par définition $\displaystyle V_n(R) = \underset{x_1^2+x_2^2+\cdots+x_n^2≤R^2}{\int\cdots\int} dx_1 dx_2\cdots dx_n$.
Séparons l'intégration en deux : $\displaystyle V_n(R) = \underset{x_1^2+x_2^2≤R^2}{\iint}\left(\underset{x_3^2+\cdots+x_n^2≤R^2-x_1^2-x_2^2}{\int\cdots\int} dx_3\cdots dx_n\right)dx_1dx_2 = \underset{x_1^2+x_2^2≤R^2}{\iint}V_{n-2}\left(\sqrt{R^2-x_1^2-x_2^2}\right)dx_1dx_2$
Passons en coordonnées polaires pour les deux premières dimensions en posant $x_1 = r\cos\theta$ et $x_2 = r\sin\theta$.
On a alors $x_1^2+x_2^2=r^2$ et $dx_1dx_2 = r dr d\theta$.
$V_n(R)$ devient :
$\displaystyle V_n(R) = \int_0^{2\pi}\int_0^R V_{n-2}\left(\sqrt{R^2-r^2}\right)rdrd\theta$
Or par symétrie et analyse dimensionnelle $V_n(a\times R) = a^nV_n(R)$, et ici, on a $V_{n-2}\left(\sqrt{R^2-r^2}\right)=V_{n-2}\left(\left(\sqrt{1-\frac{r^2}{R^2}}\right)R\right)=\left(1-\frac{r^2}{R^2}\right)^{\frac{n-2}{2}}V_{n-2}(R)$
Finalement $V_n$ se réduit à :
$ \begin{aligned} V_n(R) &= V_{n-2}(R)\int_0^{2\pi}\int_0^R \left(1-\frac{r^2}{R^2}\right)^{\frac{n-2}{2}}rdrd\theta\\\\ & = 2\pi V_{n-2}(R) \int_0^R \left(1-\frac{r^2}{R^2}\right)^{\frac{n-2}{2}}rdr\\\\ & = 2\pi V_{n-2}(R) \left[-\frac{R^2}{2}\frac{2}{n}\left(1-\frac{r^2}{R^2}\right)^{\frac{n}{2}}\right]_{r=0}^{r=R}\\\\ & = \frac{2\pi R^2}{n} V_{n-2}(R) \end{aligned} $
On va ne s’intéresser ici qu’aux $n$-boules de rayon un. Le petit programme suivant nous permet d’obtenir leurs volumes :
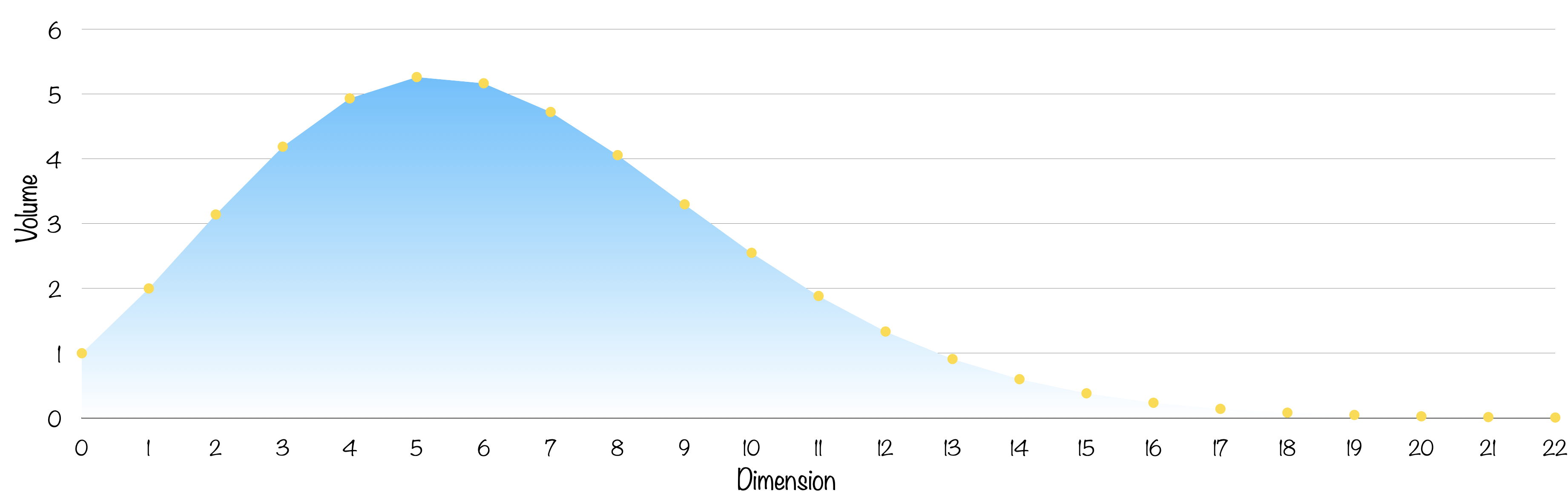
Le volume culmine en dimension 5 puis ne fait que diminuer. Qu’a de particulier la dimension 5 ? Pas grand chose…
Regardons ce que nous dit la formule de récurrence :
- si $n$ est pair :
$\displaystyle V_n(R) = \frac{2\pi R}{n}\times\frac{2\pi R}{n-2}\times\cdots\times \frac{2\pi R}{4}\times\frac{2\pi R}{2}\times V_0(R)$, avec $V_0(R) = 1$
Donc $\displaystyle V_n(R) = \frac{2^{n/2}\pi^{n/2}R^n}{n\cdot (n-2)\cdots 4 \cdot 2} = \frac{\pi^{n/2}R^n}{\left(\frac{n}{2}\right)!}$ - si $n$ est impair :
$\displaystyle V_n(R) = \frac{2\pi R}{n}\times\frac{2\pi R}{n-2}\times\cdots\times \frac{2\pi R}{3}\times\frac{2\pi R}{1}\times V_1(R)$, avec$V_1(R)=2R$
Donc $\displaystyle V_n(R) = \frac{2^{\frac{n+1}{2}}\pi^{\frac{n-1}{2}}R^n}{n\cdot (n-2)\cdots 3\cdot 1} $
L’ensemble des deux formules peuvent se combiner en une seule utilisant la fonction gamma $\Gamma$ :
$\displaystyle V_n(R) = \frac{\pi^{\frac{n}{2}}R^n}{\Gamma\left(\frac{n}{2}+1\right)} $
En traçant l’évolution du volume pour différents rayons, on constate que le maximum change de dimension.
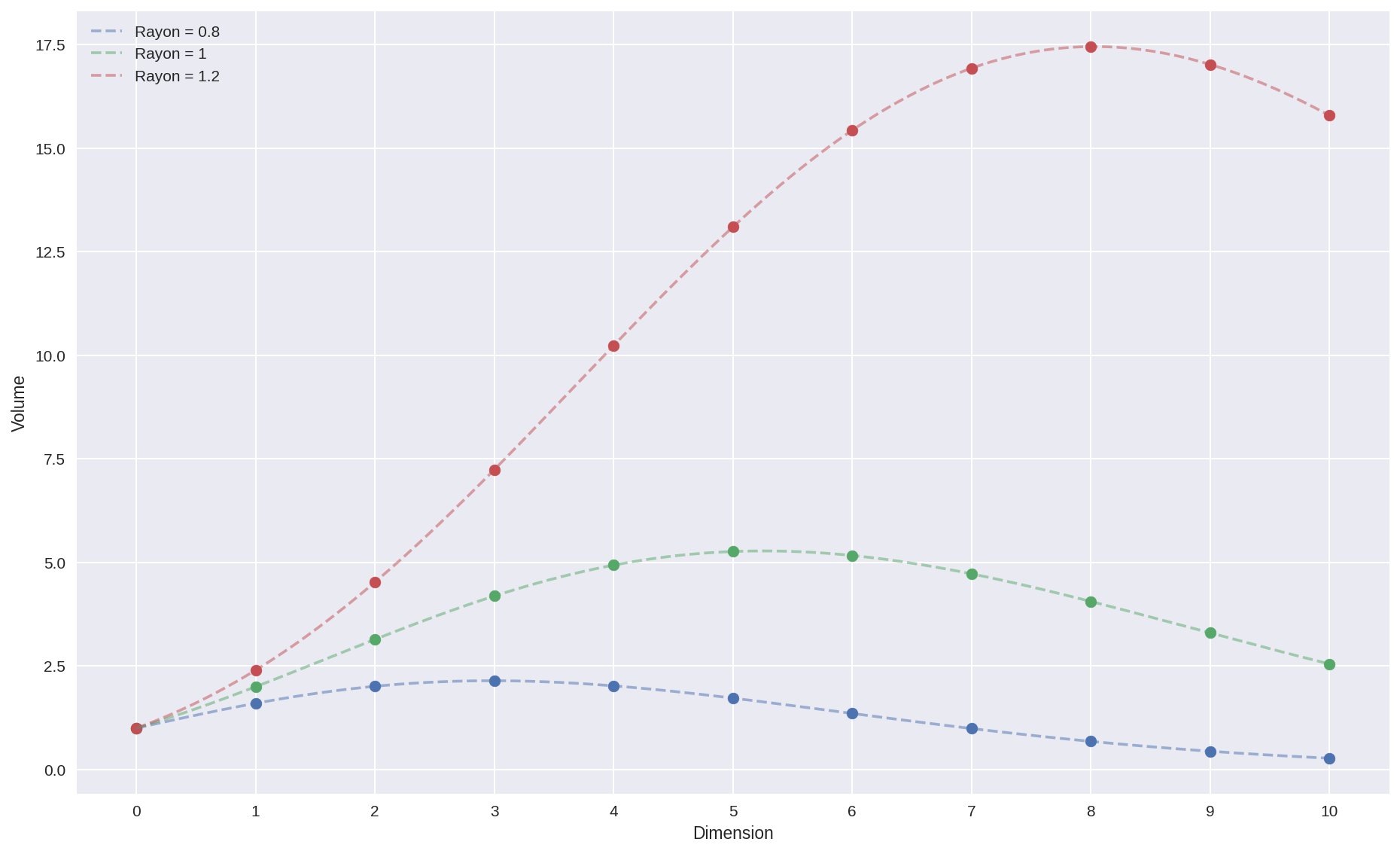
La présence d’un maximum s’explique par la course entre la tortue numérateur, à base de puissances, et le lièvre dénominateur fait de factorielles. Si les puissances peuvent démarrer plus vite, la factorielle finira toujours fatalement par dominer (dans les deux cas, on a un produit de $n$ facteurs mais pour la factorielle, la taille des facteurs augmente en fonction de $n$). Et c’est bien ça le plus intéressant : cet évanouissement du volume de l’hyperboule pour des grandes dimensions.
Essayons de mieux comprendre son origine.
Boule dans boite
Plaçons maintenant la $n$-boule de rayon 1 dans un $n$-cube de côté 2 et calculons la proportion de volume occupé par la boule (il suffit de diviser par $2^n$ le volume de la boule).
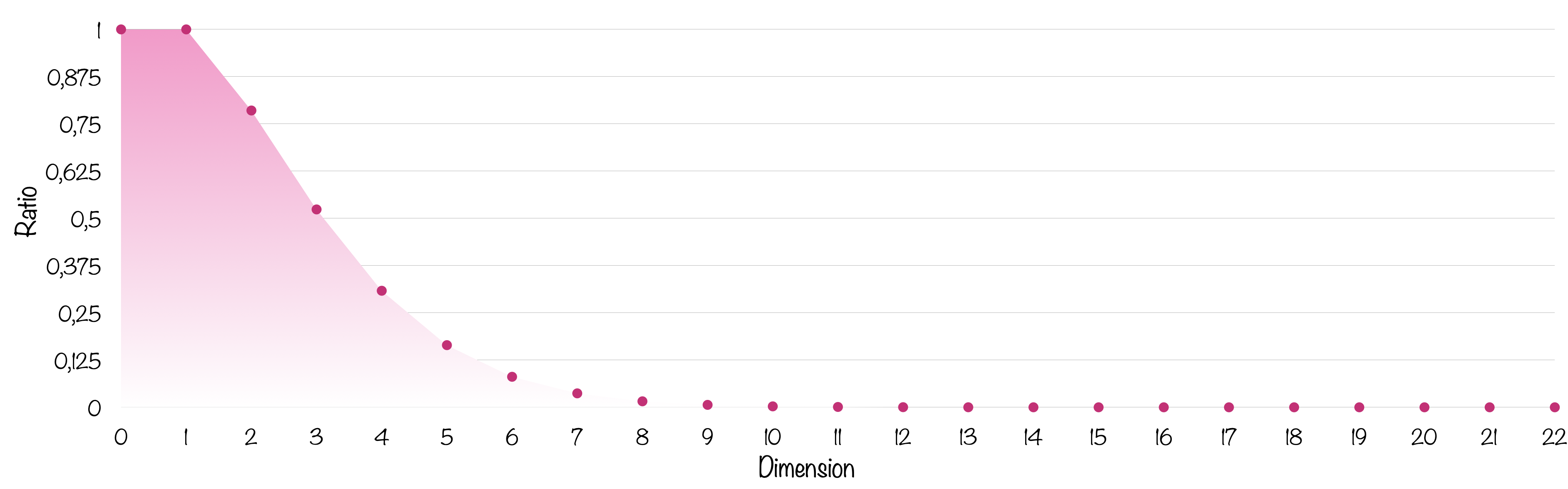
Le rapport des deux volumes s’écrabouille très très vite. Il faut une échelle logarithmique pour y voir plus clair.
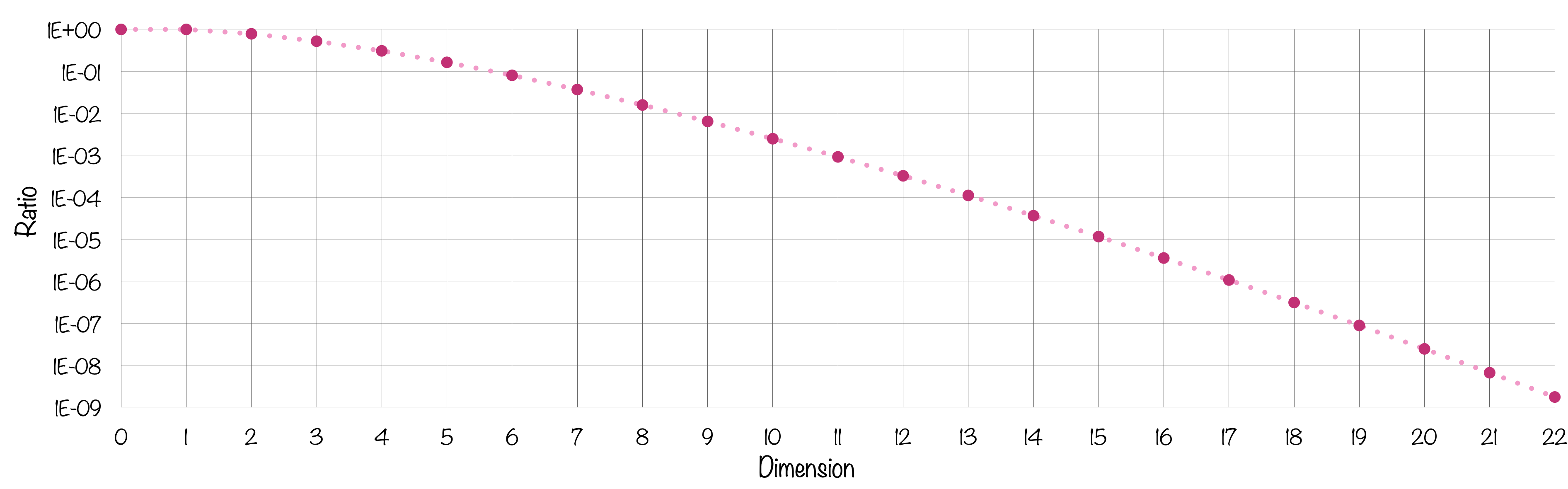
À 11 dimensions, la boule ne représente plus qu’un millième du volume de la boite et c’est environ un millionième en dimension 17, soit pas grand chose… Alors qu’il s’agit bien à chaque fois de la plus grande sphère possible calée dans la boite ! Si on augmentait son rayon d’un poil, elle déborderait.
Raison de cette apparente étrangeté : la différence entre le volume du cube et celui de la sphère est à chercher dans les coins !

Or plus la dimension augmente, plus le cube a de coins… En effet, un $n$-cube possède $2^n$ coins. Ajoutez à cela que les diagonales deviennent de plus en plus grandes ($\sqrt{n}$), et on commense à se convaincre que le volume de la sphère va vite devenir négligeable…
Concentration sur les bords
En tirant des points au hasard dans un hypercube, on va vérifier que plus la dimension augmente, plus le volume se concentre sur les bords.

Dans le petit programme suivant, on tire un million de points au hasard dans un $n$-cube de côté 1 et on calcule la proportion qui se trouve à une distance inférieure à 0,1 d’un bord. C’est facile, il suffit de checker si c’est le cas pour chaque tirage correspondant à la coordonnée sur chaque axe. Dès qu’une coordonnée est inférieure à 0,1 ou supérieure à 0,9 (on suppose ici que les coordonnées des sommets du cube sont des séquences de 0 et de 1), on compte le point.
La raison de cette concentration devient évidente à la lecture du programme ; pour qu’un point soit près d’un bords, il suffit qu’une de ses coordonnées soit près d’un bord. Or si on augmente le nombre de dimensions, on augmente par la même le nombre de coordonnées et donc le nombre de tirages. Plus la dimension augmente moins ça devient possible qu’aucune des coordonnées ne tombe près d’un bord.
Cela permet d’ailleurs d’expliquer que le volume de l’hypersphère de rayon 1 se ratatine : ses points doivent être presque tous loin des bords. En effet, la sphère touche les bords qu’au centre des faces or un hypercube de dimension $n$ compte seulement $2n$ faces (hypercubes de dimension $n-1$) pour $2^n$ sommets !
The “Average man”
Ce résultat a une conséquence très importante en science des données : augmenter le nombre de variables descriptives revient à augmenter le nombre de dimensions et donc à renforcer dans le même mouvement la probabilité d’obtenir des valeurs hors normes. Si ces variables décrivent différents aspects d’un individu, on en arrive à la conclusion que l’individu moyen n’existe pas puisqu’il y aura presque toujours au moins une de ces variables qui sortira des standards.
L’U.S. Air Force l’a découvert au prix fort à la fin des années 40. Beaucoup de pilotes se crashaient (jusqu’à 17 le même jour !), mais personne ne savait trop pourquoi… Jusqu’à ce qu’un jeune scientifique qui venait d’être engagé par l’armée, Gilbert Daniels, se résolut à mesurer tous les pilotes.

Les cockpits et les casques avaient tout spécialement été dessinés pour s’adapter parfaitement au pilote moyen… sans suspecter alors que le pilote moyen était tout à fait extraordinaire ! Ses mensurations furent obtenues au moyen d’une large campagne statistique menée sur des milliers de jeunes hommes. Mais lorsque Daniels prit les mesures d’un peu plus de 4000 pilotes sur 10 critères différents (circonférence de la poitrine, longueur d’entre-jambes, etc.) et qu’il inventoria ceux dont l’ensemble des caractéristiques s’étalait autour de la moyenne (à 30% près), il n’en trouva… aucun ! Le pilote moyen n’existe pas. Résultat, chaque pilote avait au moins un truc qui cloche par rapport au design du cockpit, ce qui rendait plus hasardeuse, semble-t-il, la maîtrise de l’avion.
Daniels reporta ses résultats dans cette étude intitulée The “Average man”?. Cela fit changer son fusil d’épaule à l’armée américaine qui se mit à adapter l’avion au pilote plutôt que l’inverse.
Distance entre les points
Une autre bizarrerie apparaît lorsqu’on regarde la distance séparant deux points pris au hasard dans un hypercube.
Les histogrammes suivant représentent la répartition des distances obtenues entre chaque paire pour 1000 points tirés au hasard uniformément dans l’hypercube. Les pointillés indiquent les distances minimales (0) et maximales ($\sqrt{n}$) possibles pour ces distances.
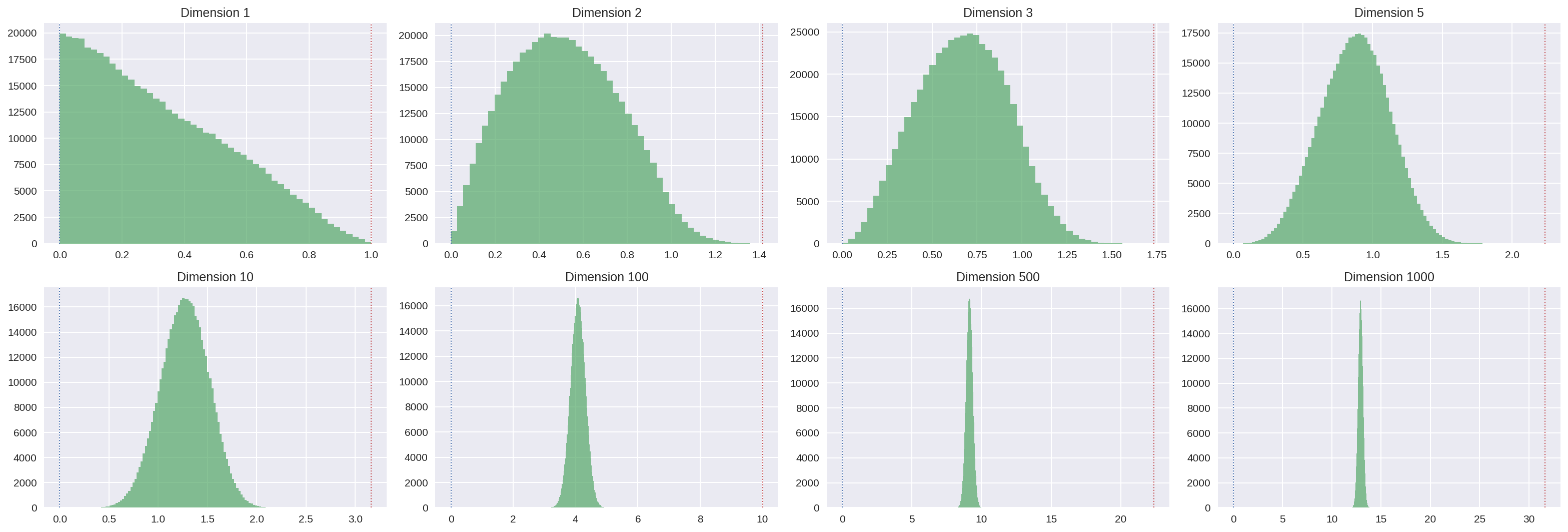
Encore de la magie noire : en grande dimension, la distance entre deux points est à peu près toujours la même !!
Ce n’est finalement pas si dur à intuiter. Tirer un point au hasard dans l’hypercube de dimension $n$ revient à choisir au hasard $n$ coordonnées pour construire un vecteur $\vec{v_1}=x_1 \vec{e_1}+x_2\vec{e_2}+\cdots + x_n\vec{e_n}$. Et on fait pareil avec un 2e point : $\vec{v_2}=x_1^\prime \vec{e_1}+x^\prime_2\vec{e_2}+\cdots + x^\prime_n\vec{e_n}$.
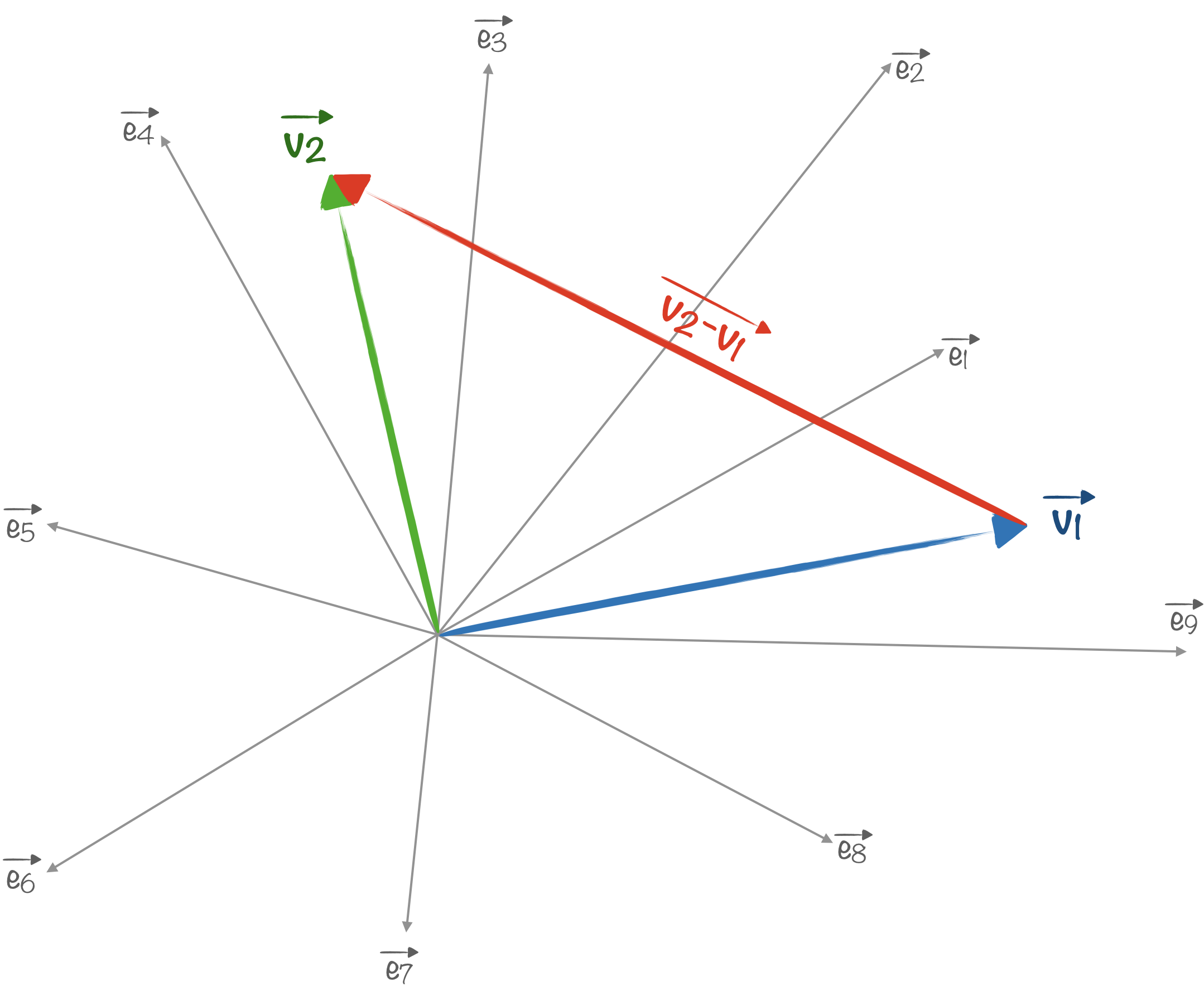
Pour $n$ grand, la probabilité que ces deux vecteurs soient orthogonaux (ce qui signifie que leurs directions sont indépendantes) devient énorme. En effet, il suffit qu’une des coordonnées soit quasiment nulle pour qu’il y ait orthogonalité et en multipliant les tirages, ça va finir par arriver.
En supposant pour simplifier que chacun des points se ballade à peu près au milieu d’une demi-diagonale de l’hypercube (puisqu’il est bourré de diagonales en grande dimension), on se retrouve avec deux vecteurs orthogonaux éloignés de $\frac{\sqrt{n}}{4}$ du centre. Leur distance sera donc approximativement $\sqrt{\left(\frac{\sqrt{n}}{4}\right)^2+\left(\frac{\sqrt{n}}{4}\right)^2}=\frac{1}{2\sqrt{2}}\sqrt{n}\approx 0,35\sqrt{n}$. La distance entre deux points augmenterait ainsi comme la racine carrée du nombre de dimensions.
En ajustant la courbe obtenue en traçant la distance moyenne par une fonction $a\sqrt{n}$, l’accord est plutôt très bon ! On obtient $a=0,41$. Pour le coup, ce n’est pas tout à fait nos $0,35$ mais pour un modèle ultra simplifié, on n’est pas si loin…
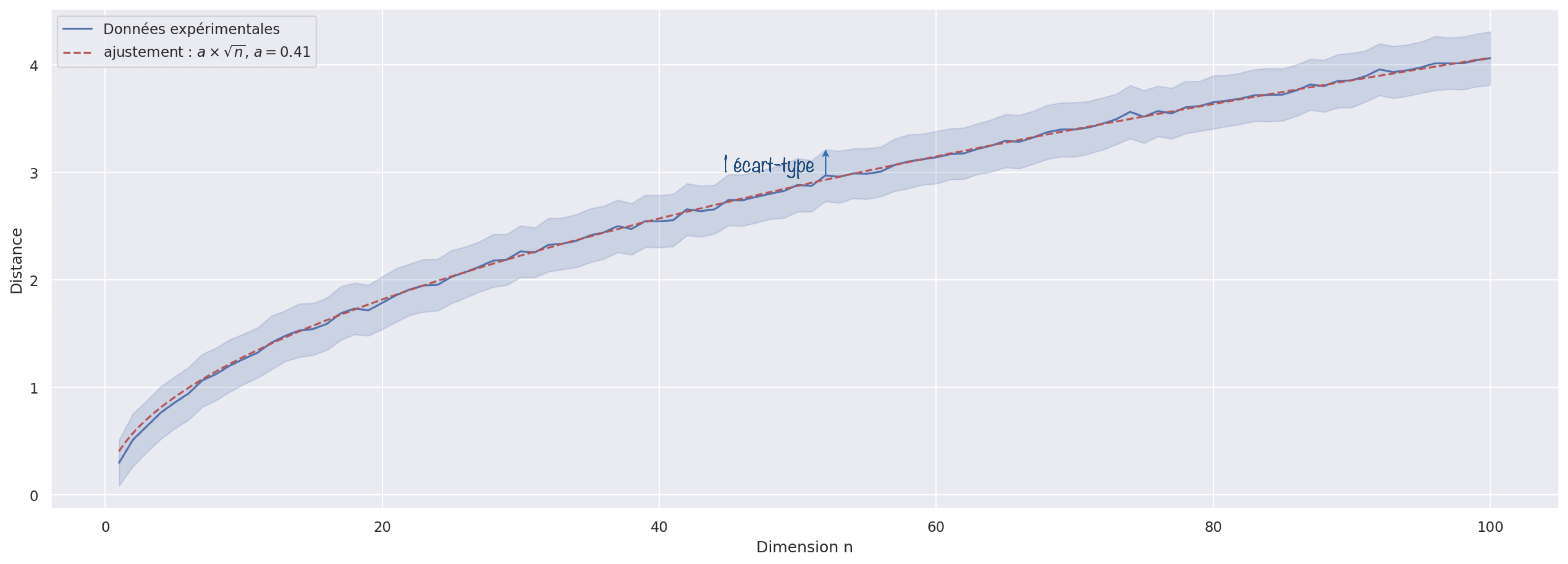
On constate par contre que la variabilité, incarnée par l’écart-type, n’est pas modifiée ! C’est ce qui explique que la variabilité relative devient, elle, de plus en plus faible quand le nombre de dimensions augmente.
La raison de cette conservation de l’écart-type est à chercher du côté de son évolution inversement proportionnelle à la racine carrée du nombre d’échantillons.
Or ici, le nombre d’échantillons correspond à la dimension. Par conséquent l’augmentation de la variabilité provoquée par l’augmentation des distances ($\propto\sqrt{n}$) est compensée par la diminution de cette même variabilité du fait de l’augmentation du nombre de tirages ($\propto 1/\sqrt{n}$) .
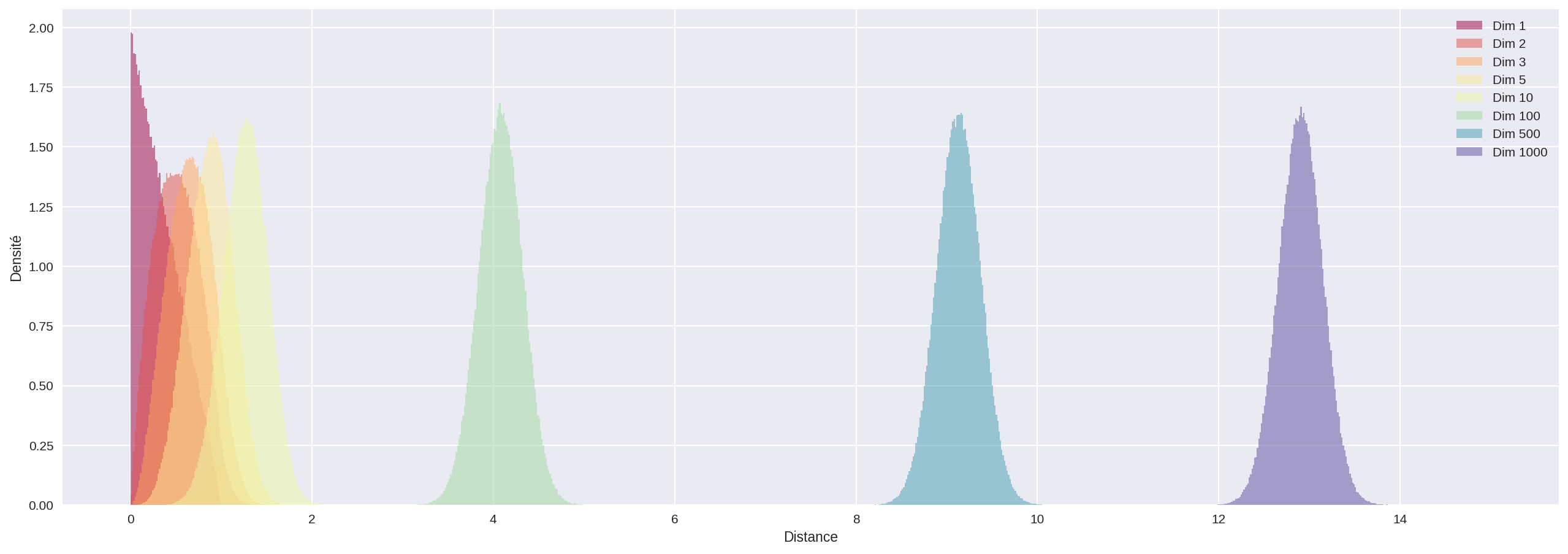
On comprend mieux pourquoi un algorithme comme KNN qui vise à prédire une valeur ou catégorie en regardant celle des plus proches voisins galère à grande dimension ; tous les voisins sont à peu près à la même distance…