Le triangle
Pythagore
Pythagore a vécu à Samos (une île grecque) au 6e siècle avant notre ère. Malgré le nom qu’on lui donne, le théorème de Pythagore était connu et utilisé par les Babyloniens et les Indiens des siècles avant Pythagore. Mais peut-être que Pythagore a été le premier à l’introduire en Grèce et cela a suffi à lui octroyer une reconnaissance éternelle.
- Théorème de Pythagore :
Si un triangle est rectangle, alors le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. - Réciproque du théorème de Pythagore :
Si dans un triangle le carré de la longueur du plus grand côté est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle. - Contraposée du théorème de Pythagore :
Si dans un triangle le carré de la longueur du plus grand côté n’est pas égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle n’est pas rectangle. - Contraposée de la réciproque du théorème de Pythagore :
Si un triangle n’est pas rectangle, alors le carré de la longueur du plus grand côté n’est pas égal à la somme des carrés des longueurs des deux autres côtés.
La démonstration historique par Euclide du théorème de Pythagore :
Deux démonstrations par découpage et réarrangement :
Ces deux démonstrations par découpage (et toutes leurs cousines) reposent sur la possibilité de paver le plan avec deux carrés de côtés différents.
Une démonstration plus “physique” (reposant sur ce qu’implique une relation de proportionnalité sur une surface) :
Histoire du théorème :
Mésopotamie
Les historiens des mathématiques et assyriologues ont découvert à la fin des années 1920 que s’était forgée en Mésopotamie (l’ancien Irak), à l’époque paléo-babylonienne une culture mathématique dont l’objet n’était pas purement utilitariste.
Plusieurs des tablettes d’argile qui ont été retrouvées et analysées montrent que la relation entre les longueurs des côtés du rectangle et celle de sa diagonale (soit entre les longueurs des côtés d’un triangle rectangle) était connue et utilisée pour résoudre des problèmes calculatoires.
Des “tablettes cadastrales” (dont la plus ancienne date de -2340 à -2200 ) établies pour le commerce ou l’administration de parcelles exposent ainsi cette connaissance. La tablette Si427 datant de -1900 à -1600, découverte à Sippar (Irak), montre ainsi un terrain avec tour, aire de battage et marécage dont une des parcelles a été mise en vente par son propriétaire. Elle présente des découpes de trapèzes et de triangles rectangles ainsi que quelques triplets pythagoriciens.
La tablette Plimpton 322 datant de vers -1800 donne une liste ordonnée de nombres associés à des triplets pythagoriciens, soit des entiers (a, b, c) satisfaisant la relation a2 + b2 = c2. La tablette ne donne que deux nombres du triplet, mais les associe explicitement au plus petit côté et à la diagonale d’un rectangle. La première colonne ne contient pas un de 3 éléments du triplet mais une combinaison des 3 dont l’interprétation varie selon les hypothèses et les reconstitutions des parties manquantes. Ce pourrait être une tablette d’exercice pour étudiant mais la régularité des éléments laissent penser à une table. Les inscriptions sont en caractère cunéiforme, en base 60 avec numérotation de position.
Il n’y a pas trace de l’énoncé d’un théorème, et les historiens préfèrent souvent utiliser un autre mot, certains parlent par exemple de « règle de Pythagore ». Ni celle-ci, ni le principe qui la sous-tend ne sont explicitement énoncés non plus, mais les exemples montrent bien qu’une règle générale est connue.
La datation et l’origine exacte des tablettes d’argile n’est pas toujours évidente, beaucoup de celles-ci ont été achetées sur le marché des antiquités comme la tablette Plimpton 322, mais les historiens peuvent s’appuyer sur des éléments linguistiques, et les similarités avec celles dont l’origine est connue, ayant été obtenues par des fouilles archéologiques régulières. Les traces que l’on a des cultures antérieures rendent peu vraisemblable la découverte de la « règle de Pythagore », avant -2300, celle-ci pourrait apparaître entre -2025 et -1825.
Inde
En Inde, un énoncé du théorème, sous sa forme la plus générale, apparaît dans l’Apastamba, l’un des Śulba-Sūtras, ces traités du cordeau qui codifient les règles des constructions destinées aux rituels védiques. Ceux-ci ont été rédigés entre le viiie et le ive siècle avant notre ère (par ailleurs certains triplets pythagoriciens sont mentionnés dans des textes bien antérieurs). Les Sulbasutras parlent du rectangle et de sa diagonale, plutôt que de triangle.
Chine
Le théorème apparaît également en Chine dans le Zhoubi suanjing (« Le Classique mathématique du Gnomon des Zhou »), un des plus anciens ouvrages mathématiques chinois. Ce dernier, écrit probablement durant la dynastie Han (206 av. J.-C. à 220), regroupe des techniques de calcul datant de la dynastie Zhou (xe siècle av. J.-C. à -256). Le théorème ou procédure s’énonce de la manière suivante :
« En réunissant l’aire (mi) de la base (gou) et l’aire de la hauteur (gu), on engendre l’aire de l’hypoténuse. »
Mais la question se pose de savoir si ce théorème — ou cette procédure — était muni ou non d’une démonstration. Sur ce point les avis sont partagés. Le théorème, sous le nom de Gougu (à partir des mots « base » et « altitude »), est repris dans le Jiuzhang suanshu (Les neuf chapitres sur l’art mathématique, 100 av. J.-C. à 50), avec une démonstration, utilisant un découpage et une reconstitution, qui ne ressemble pas à celle d’Euclide et qui illustre l’originalité du système démonstratif chinois.
Source : Wikipédia

Deux vieux exos
- Un problème babylonien
Ce problème a été découvert sur des tablettes d’argile babylonienne entre -2000 et -1600.
une perche est posée verticalement contre un mur. Si son extrémité haute glisse de 6 unités vers le bas contre le mur, de combien d’unité glisse horizontalement l’extrémité basse ?

Réponse (cliquer pour afficher)
18
- Un problème chinois
Un problème plus difficile datant d’entre -250 et +50 (en Chine, le théorème de Pythagore se nomme Goo Gu 勾股).
Dans une mare, un lotus dépasse de 10 cm à la verticale. Un coup de vent le pousse de 60 cm et la fleur touche alors la surface. Quelle est la profondeur de la mare ?
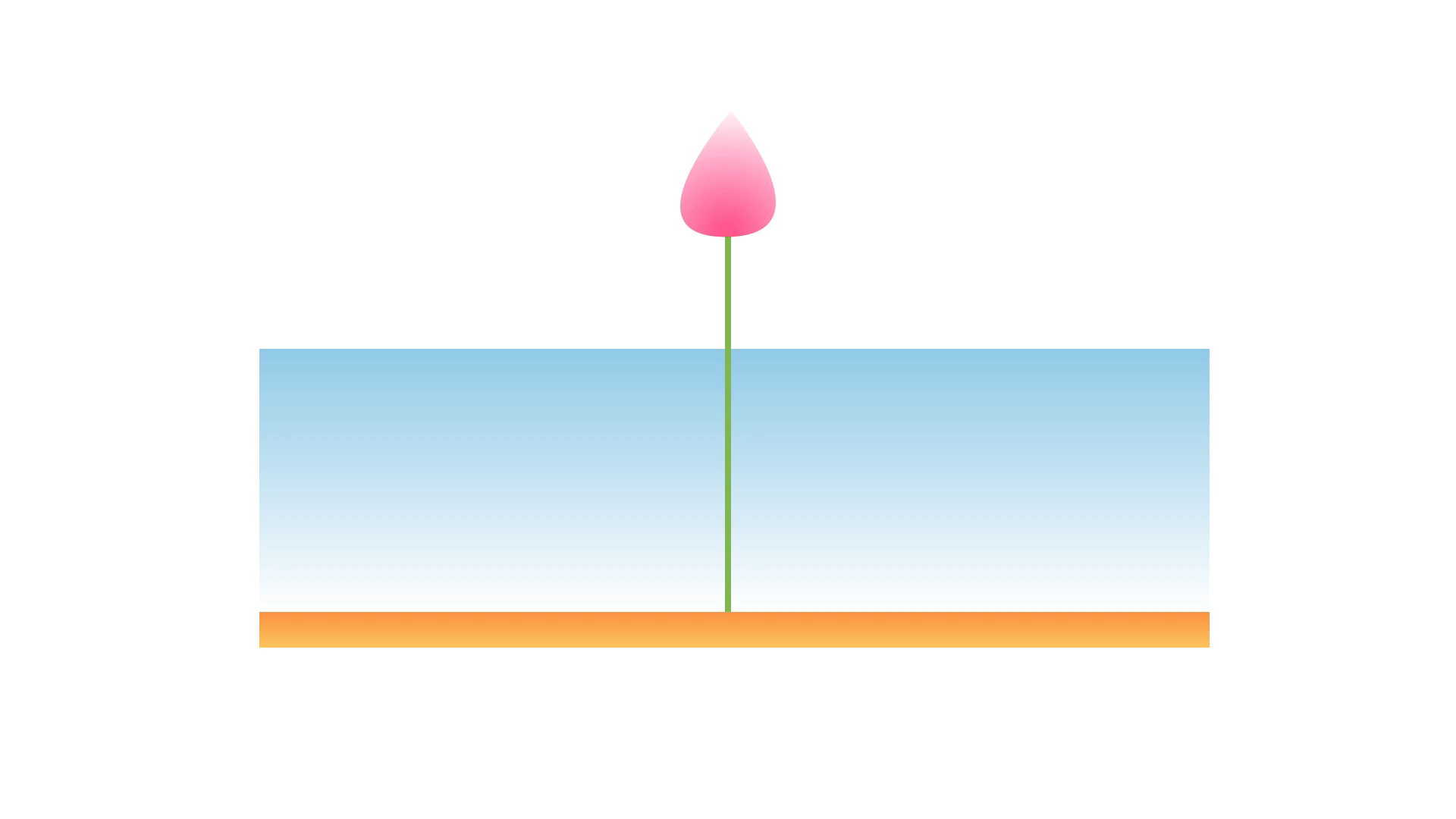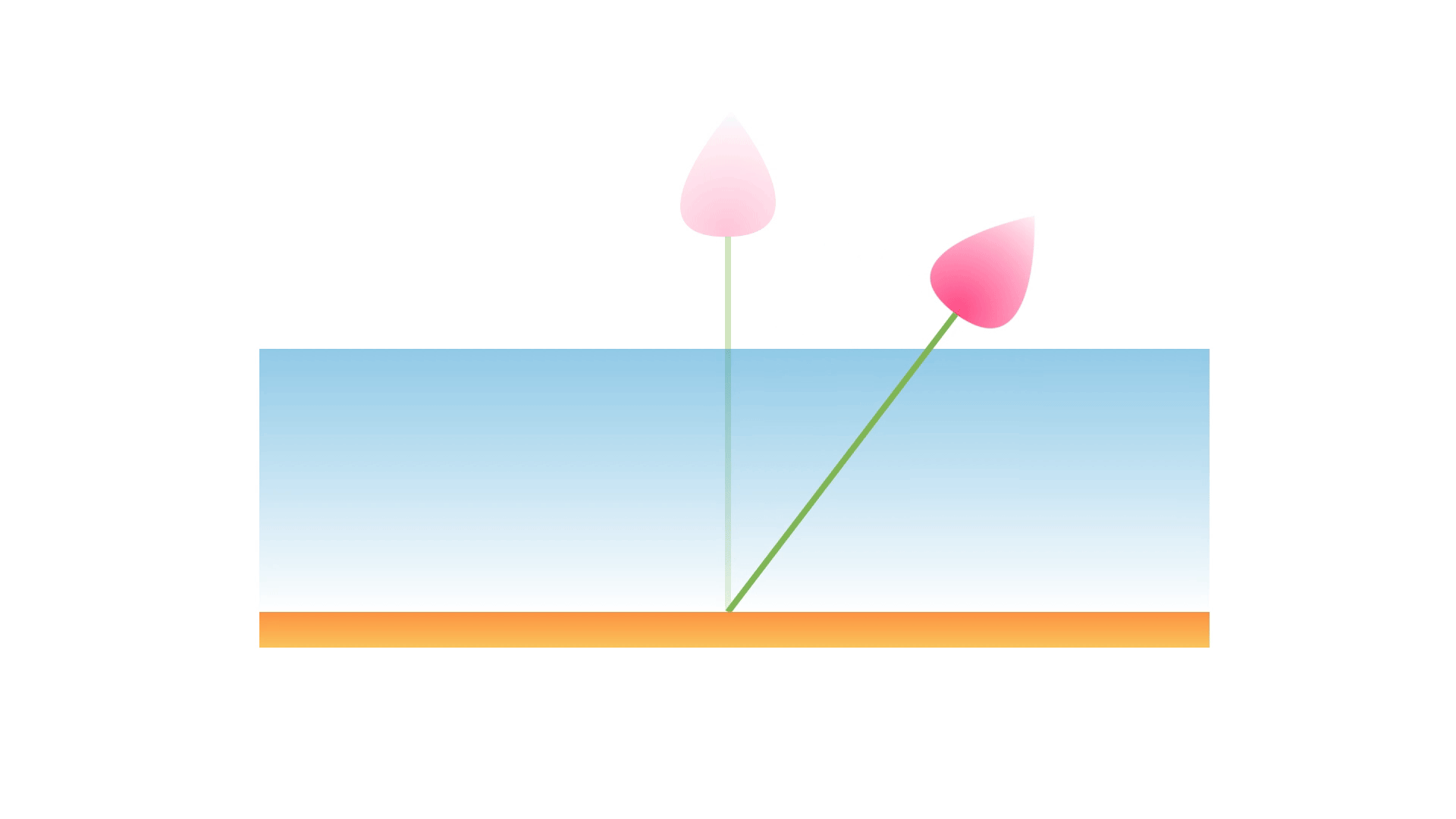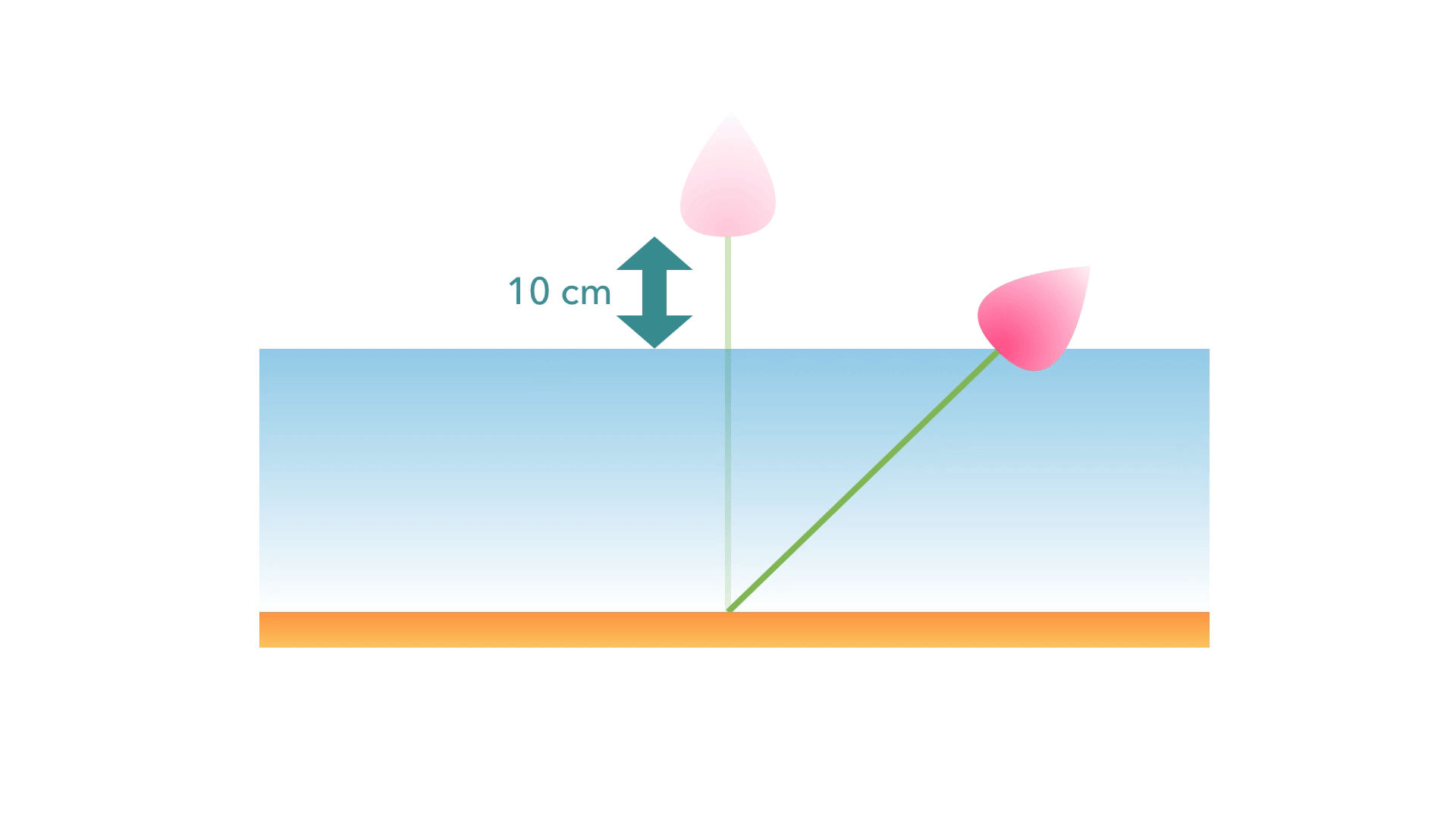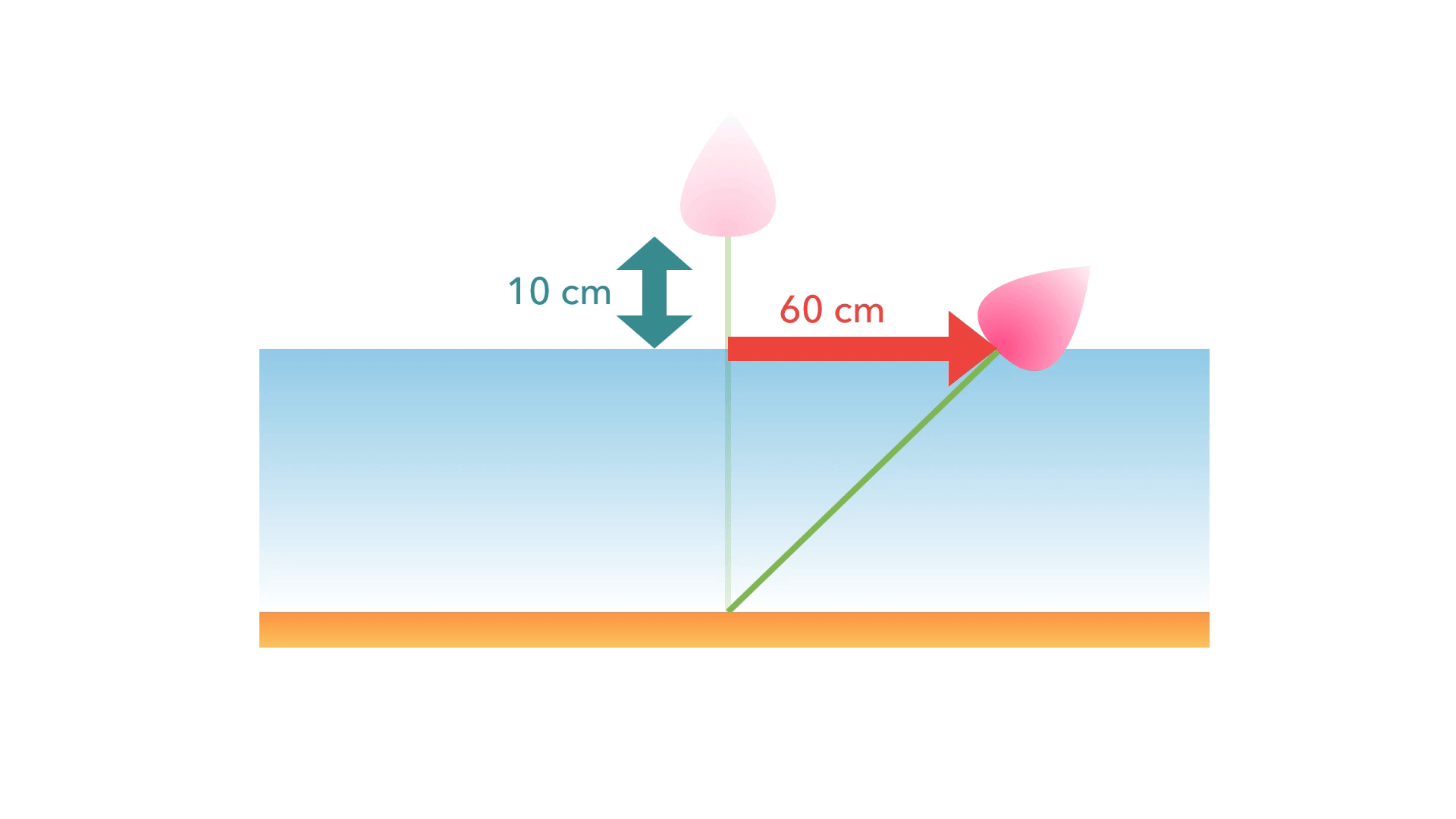
Réponse (cliquer pour afficher)
175 cm
Le théorème de Pythagore peut aussi nous aider à trouver la distance de l’horizon comme dans cette activité.

Escargot de Pythagore
L’escargot de Pythagore, spirale de Théodore ou encore spirale d’Anderhub est une figure qui permet de construire géométriquement les racines carrées des entiers consécutifs.
Cette construction est utilisée dans la jolie preuve de la dépendance en $v^2$ de l’énergie cinétique par Johann Bernoulli.
Thalès
Deux triangles semblables (ayant les mêmes angles) ont leurs côtés correspondants proportionnels. On parle de théorème de Thalès lorsque les deux triangles partagent un sommet.
L’histoire de Thalès et de la pyramide serait en fait une légende et Thalès de Millet n’aurait pas grand chose à voir avec le théorème qui porte son nom.
Certains textes de l’Antiquité grecque font référence aux travaux de Thalès de Milet au vie siècle av. J.-C., dont aucun écrit ne nous est parvenu. Cependant, aucun texte ancien n’attribue la découverte du théorème de Thalès à celui-ci. L’attribution en France du théorème à Thalès semble associée à la mesure de la hauteur d’une pyramide égyptienne que celui-ci aurait effectuée.
Dans son commentaire sur les Éléments d’Euclide, Proclus affirme que la géométrie avait été découverte en Égypte, et transportée en Grèce par Thalès après son voyage dans cette contrée. Selon une anecdote rapportée par Pline l’Ancien, Plutarque et Diogène Laërce, lors de ce voyage Thalès aurait obtenu la hauteur d’une des pyramides en mesurant l’ombre de celle-ci. Pour Pline de même que pour Diogène Laërce (qui se réfère à Hieronymus de Rhodes, un auteur actif au iiie siècle av. J.-C., ce qui est déjà autour de trois siècles après Thalès), Thalès attend que son ombre soit égale à sa taille pour mesurer l’ombre de la pyramide dont il déduit alors la hauteur.
« Hiéronyme dit que Thalès mesura les pyramides d'après leur ombre, ayant observé le temps où notre propre ombre égale notre hauteur. »La version que donne Plutarque dans Le Banquet des Sept Sages est clairement romancée :
« Ainsi, vous, Thalès, le roi d'Égypte vous admire beaucoup, et, entre autres choses, il a été, au-delà de ce qu'on peut dire, ravi de la manière dont vous avez mesuré la pyramide sans le moindre embarras et sans avoir eu besoin d'aucun instrument. Après avoir dressé votre bâton à l'extrémité de l'ombre que projetait la pyramide, vous construisîtes deux triangles par la tangence d'un rayon, et vous démontrâtes qu'il y avait la même proportion entre la hauteur du bâton et la hauteur de la pyramide qu'entre la longueur des deux ombres. »La version de Plutarque fait intervenir des rapports de proportionnalité, et donc peut renvoyer au théorème de Thalès. Ce n’est pas vraiment le cas de la version plus élémentaire rapportée par Pline et Diogène Laërce, qui correspond très probablement à la version originale de Hieronymus. De toute façon, comme le remarque Maurice Caveing, « il est peu vraisemblable que le souverain d’un pays qui, plus de 1 000 ans avant Thalès, connaissait le calcul du seqed, ait ignoré comment mesurer la hauteur des pyramides ».
Source : Wikipédia
La vidéo suivante présente une démonstration du théorème de Thalès et de sa réciproque (permettant de s’assurer du parallélisme entre deux droites) à partir de calculs d’aires de triangles.
Grâce au théorème de Thalès, on peut partager de manière égale un segment sans faire la moindre mesure.
Présentation d’un petit problème posé à l’examen d’entrée au MIT (grande université scientifique américaine) en 1869 :
Grâce à Thalès, on peut aussi savoir si deux bateaux vont se rencontrer (on dit faire route de collision).
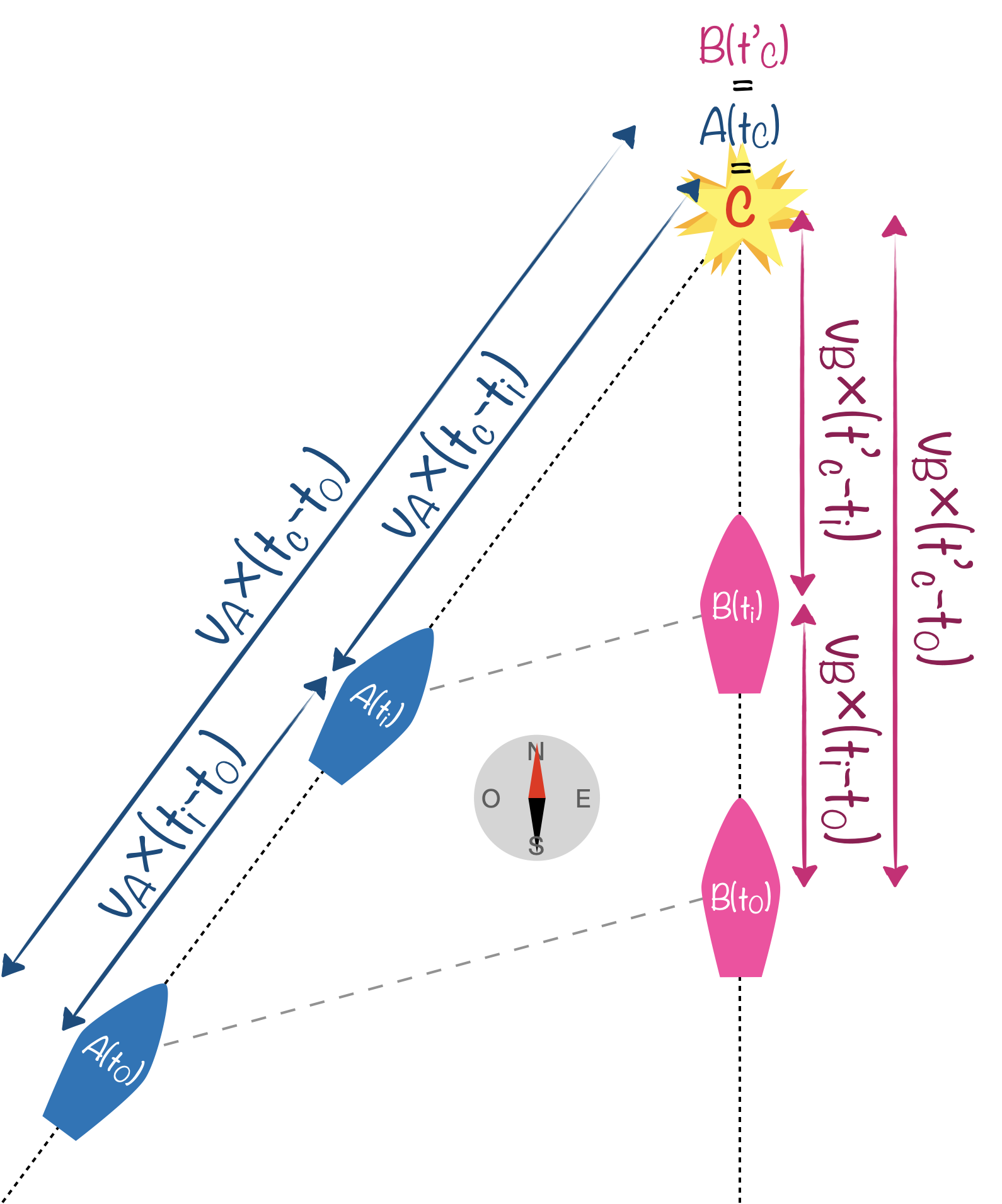
Supposons qu’un bateau A avance selon un cap fixe (direction constante) à vitesse constante et continue de voir dans la même direction un bateau B, lui aussi en mouvement rectiligne uniforme (suffit de remarquer que le bateau B reste aligné avec un repère fixe pris sur le bateau A). Alors les droites joignant les deux bateaux à un instant donné sont parallèles.
Appelons C le point de croisement entre les deux trajectoires des bateaux et appelons $t_C$ et ${t’}_C$ les instants respectifs où les bateaux A et B arrivent en C.
Appliquons le théorème de Thalès :
$$\frac{A(t_C)A(t_i)}{A(t_C)A(t_0)}=\frac{B({t’}_C)B(t_i)}{B({t’}_C)B(t_0)} \Rightarrow\frac{v_A(t_C-t_i)}{v_A(t_C-t_0)}=\frac{v_B({t’}_C-t_i)}{v_B({t’}_C- t_0)}$$
On en déduit $t_C = {t’}_C$, ce qui implique que les deux bateaux arrivent ensemble en C. Il va y avoir collision ! Donc si on voit un bateau toujours dans la même direction, la plus grande méfiance s’impose.