Logique modale
En logique modale, un “monde possible” contient les propositions qui sont vraies dans ce monde. Il correspond à un modèle du calcul des propositions (à une ligne d’une table de vérité). Ces mondes possibles sont connectés entre eux par des relations d’accessibilité, et les opérateurs de modalité permettent d’explorer ces relations. Si $P$ est vraie dans tous les mondes accessibles depuis le monde $a$, alors on écrit $a\Vdash \Box P$ et si $P$ est vraie dans au moins un de ces mondes, on utilise $a\Vdash \Diamond P$. Un modèle de la logique modale est alors un graphe orienté, appelé système de transition ou structure de Kripke.
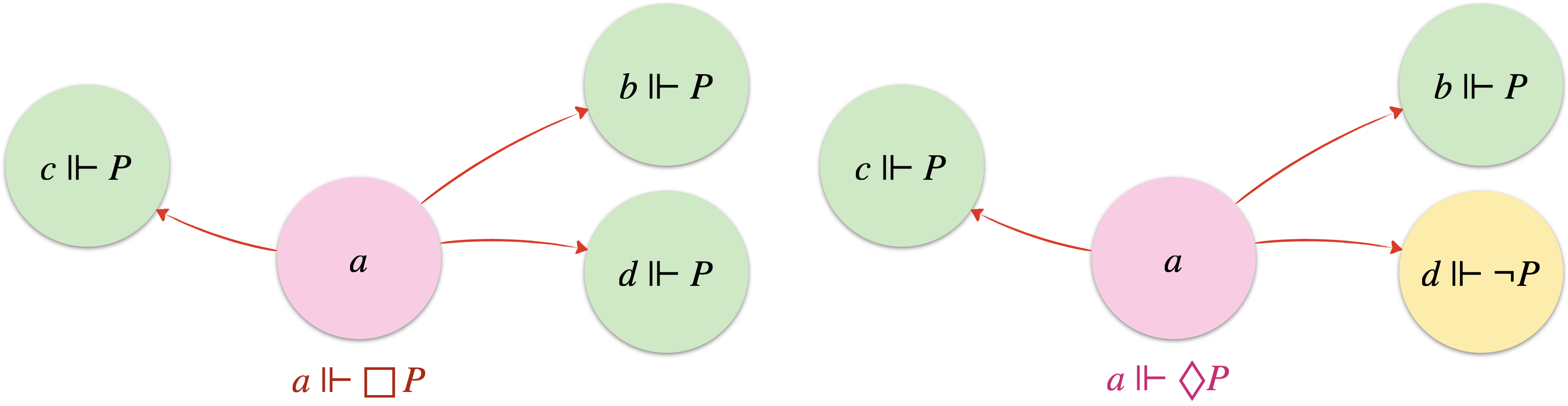
Avec pour axiomes les tautologies du calcul des propositions auxquelles on ajoute l'axiome modal $\text{(K)}$ (qui distribue $\Box$ dans une implication), et les règles de nécessitation (si $\vdash\phi$, alors on a aussi $\vdash\Box\phi$), de substitution uniforme (une formule prouvable où toute occurence d'une proposition est remplacée par une même formule quelconque est tout autant prouvable) et de modus ponens pour assurer la cohérence de la machinerie, on se retrouve avec la logique modale normale de base $\mathbf{K}$ qui permet de produire l'ensemble des formules universellement vraies. Toute formule obtenue dans $\mathbf{K}$ est vraie dans tout monde possible de toute structure de Kripke, et inversement. On dit alors qu'il y a correction et complétude entre le système formel et les modèles associés : $\vdash_\textbf{K}\phi$ ssi $\Vdash_\mathscr{C}\phi$ où $\vdash_\textbf{K}\phi$ dit que $\phi$ a été prouvée dans $\mathbf{K}$, et $\Vdash_\mathscr{C}\phi$ dit que $\phi$ est valide (vraie dans tout monde) pour tout modèle de la classe $\mathscr{C}$ qui désigne l'ensemble des systèmes de transition.
En ajoutant de nouveaux axiomes modaux au système formel, on ajoute par là même des contraintes aux modèles associés (les graphes gagnent de nouvelles propriétés). À chaque jeu d'axiomes va correspondre une certaine classe de systèmes de transition où la vérité pourra se déployer. En ajoutant l'axiome $\text{(B)}=P\rightarrow \Box\Diamond P$, par exemple, la validité des formules obtenues sera limitée aux graphes non orientés $\mathscr{C}_{sym.}$ puisque l'axiome $\text{(B)}$ ajoute la symétrie aux structures.
Les différentes logiques modales
On cherche maintenant à incarner la logique modale avec des interprétations précises des opérateurs modaux. La boîte peut servir à exprimer qu’un agent sait quelque chose et son dual, le diamant, exprime alors le fait que cet agent croit seulement possible cette même chose. Ça nous place dans une logique épistémique (logique de la connaissance) et c’est principalement cette version qu’on a utilisée jusqu’ici pour donner corps à la théorie. Mais d’autres emplois sont courants et ne rattachent pas forcément les opérateurs modaux à un agent, comme c’est le cas de la logique aléthique et la logique déontique. On verra aussi qu’en fonction des interprétations, certains axiomes sont plus naturels que d’autres et donc que ces différentes logiques modales s’épanouissent dans des univers aux topologies différentes.
Logique aléthique
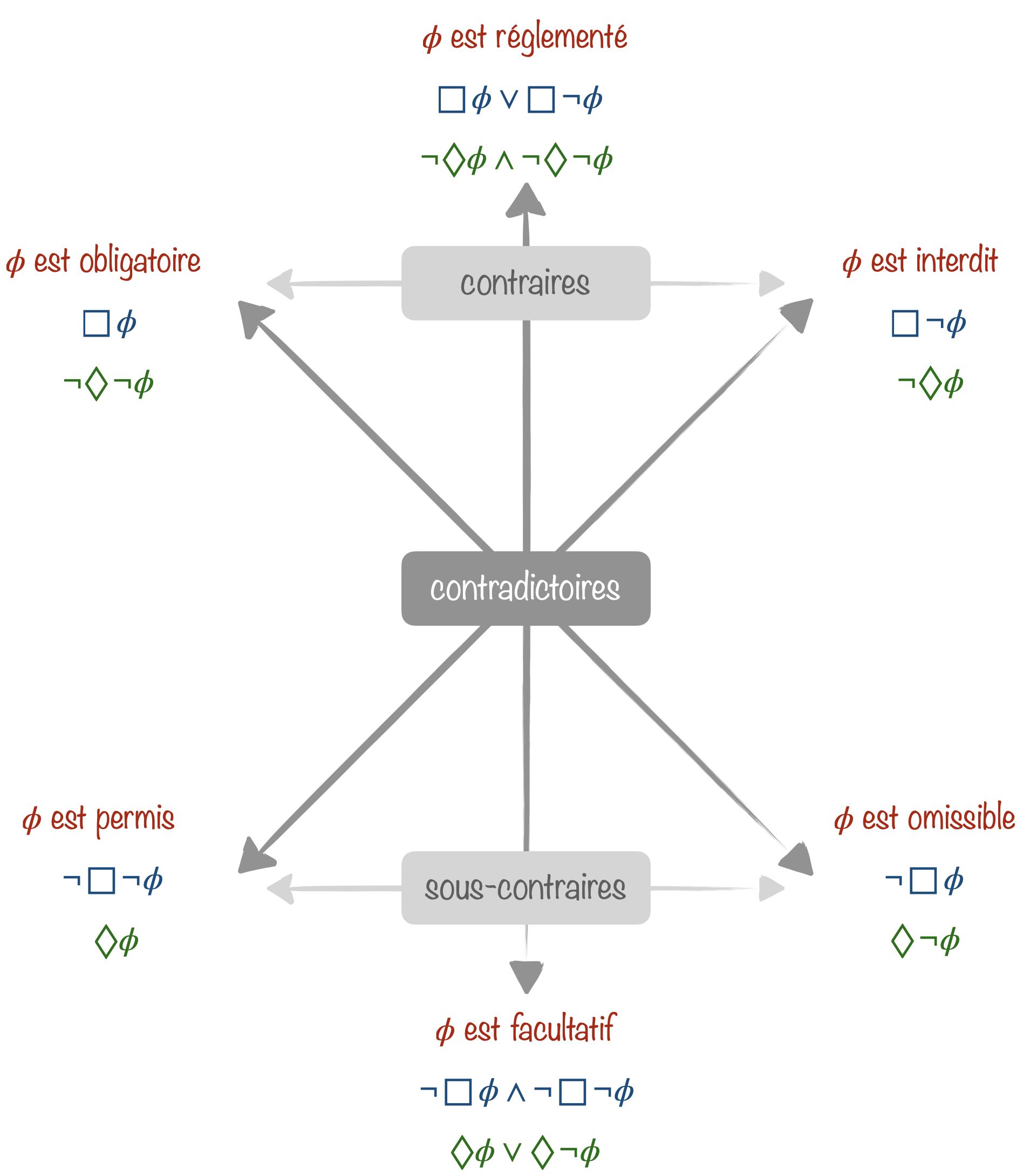
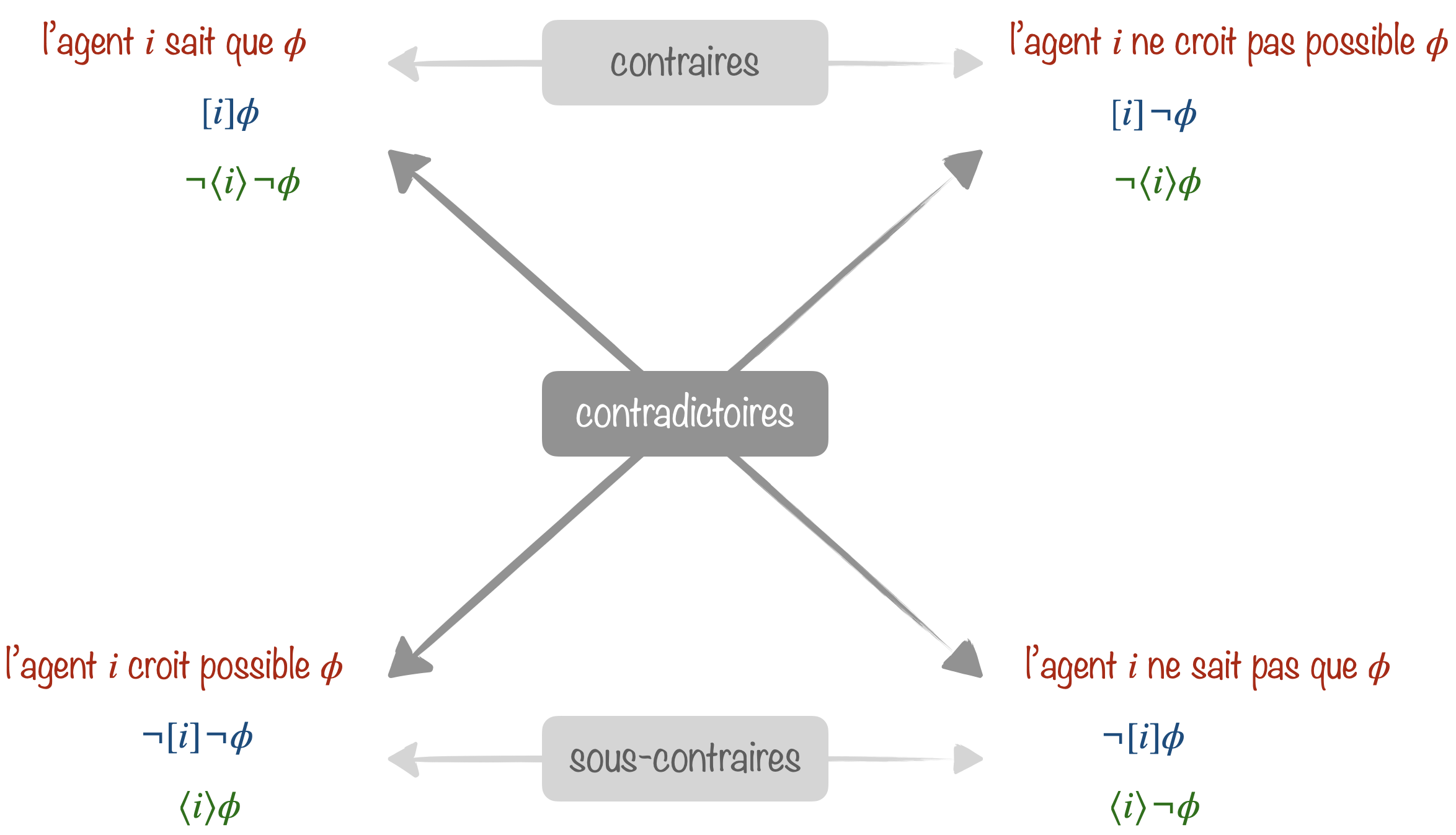
La logique modale est dite aléthique lorsque les opérateurs modaux traduisent la nécessité et la possibilité.

Les trois cellules rectangulaires sont destinées à être conjointement exhaustives et mutuellement exclusives : chaque proposition peut être nécessaire, contingente (possiblement vraie mais aussi possiblement fausse), ou encore impossible, mais jamais plus qu’un de ces trois choix.
On peut en déduire l’hexagone logique suivant, extension du carré des oppositions d’Aristote, dû à Sesmat et Blanché :
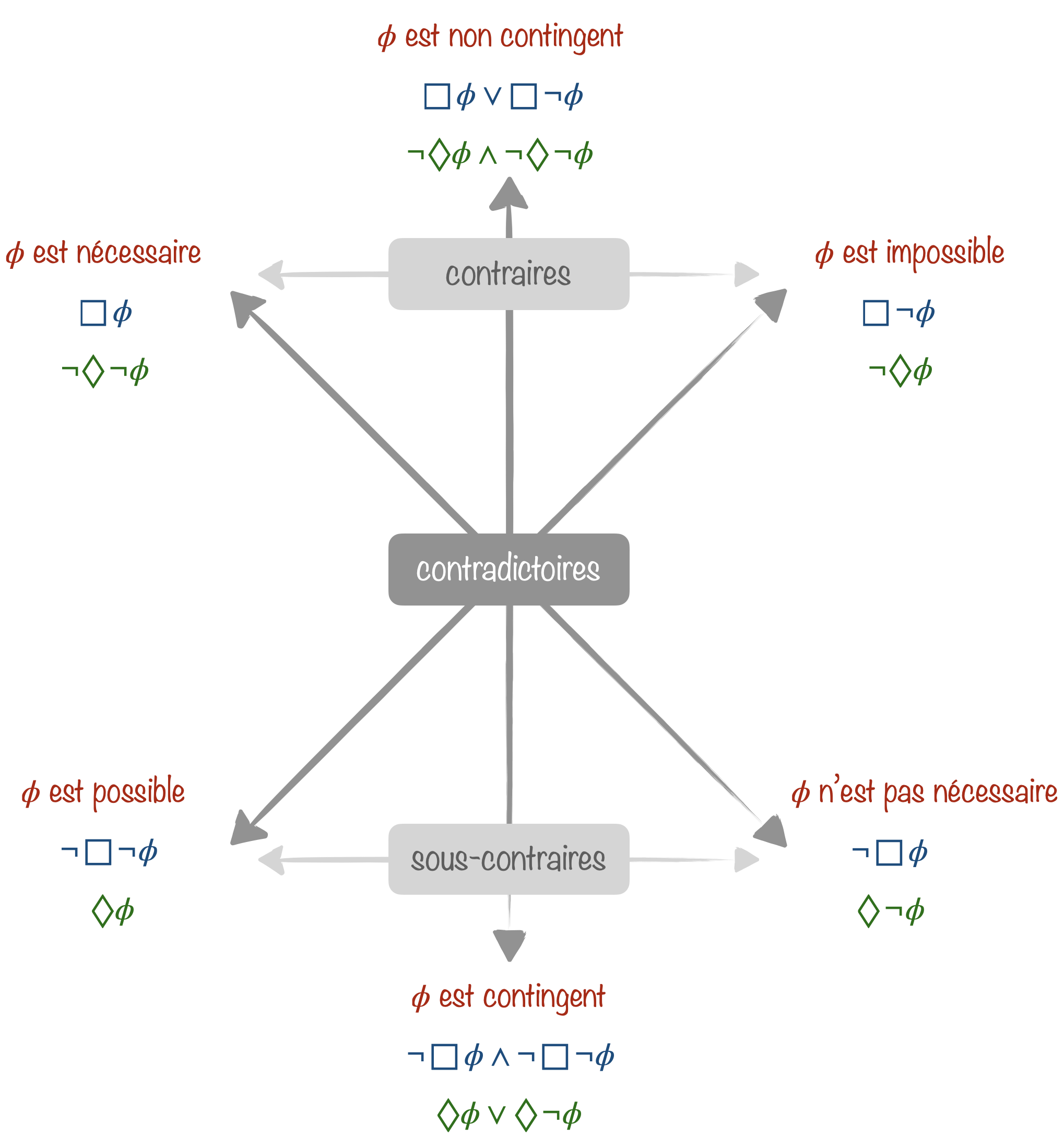
- Deux propositions contradictoires ne sont jamais ni vraies, ni fausses en même temps.
- Deux propositions contraires ne sont jamais vraies en même temps, mais peuvent être fausses en même temps.
- Deux propositions sous-contraires ne sont jamais fausses en même temps, mais peuvent être vraies en même temps.
L’axiome $\text{(K)}=\Box(P\rightarrow Q)\rightarrow(\Box P\rightarrow\Box Q)$, qui rappelons-le est vrai dans tout système, se traduit en logique aléthique par “s’il est nécessaire que $P$ entraîne $Q$, alors si $P$ est nécessaire, $Q$ est nécessaire également.”
Parmi les autres axiomes qu’on a pu rencontrer, deux semblent plus adaptés à cette interprétation de la modalité :
- l'axiome $\text{(T)}=\Box P\rightarrow P$ : "s'il est nécessaire que $P$, alors $P$ est réalisée" (les logiciens du Moyen Âge, déjà, employaient la formule ab necesse esse).
- l'axiome $\text{(B)}= P\rightarrow \Box\Diamond P$ : "si $P$ est réalisée, alors il est nécessaire que $P$ soit possible" (cela semble en effet assez naturel).
Le système logique normale adapté à la logique aléthique semble donc être $\textbf{KBT}$ et la classe de modèles adaptée est donc celle des systèmes de transition à la fois réflexifs et symétriques.

Aristote est à l’origine de la logique aléthique et il en donne un exemple célèbre dans De l’interprétation :
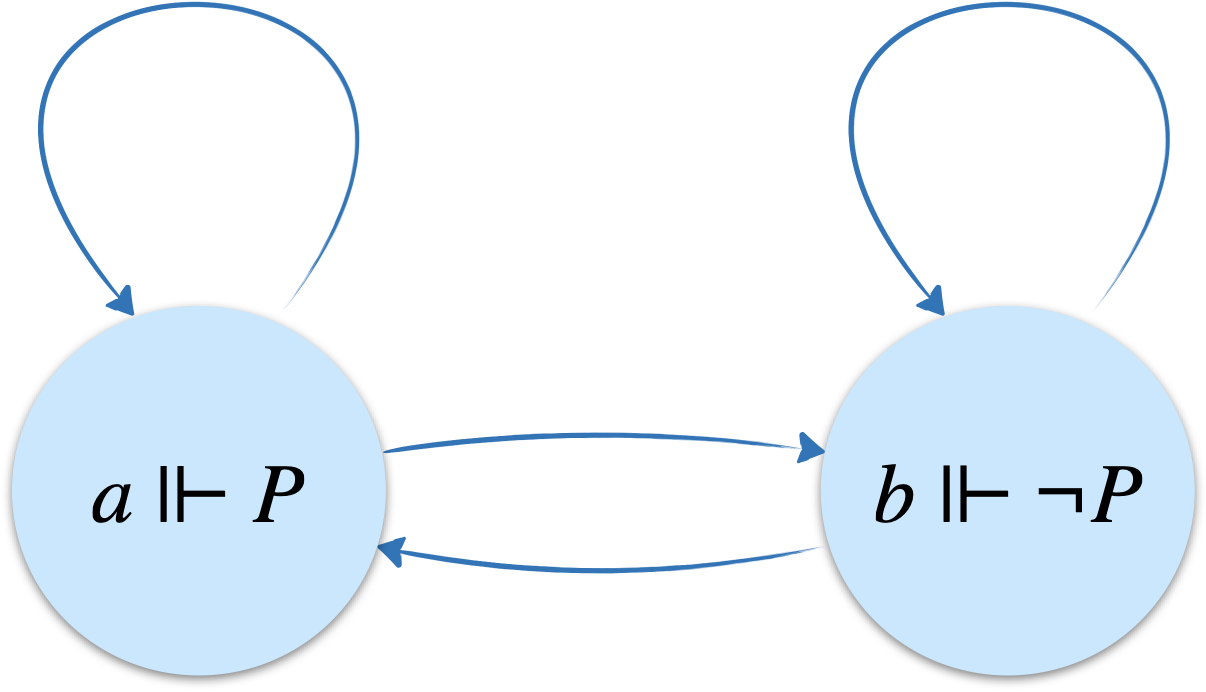
Nécessairement il y aura demain une bataille navale ou il n’y en aura pas. Mais il n’est pas nécessaire qu’il y ait demain une bataille navale, pas plus qu’il n’est nécessaire qu’il n’y en ait pas. Mais qu’il y ait ou qu’il n’y ait pas demain une bataille navale, voilà qui est nécessaire.
En appelant $P$ l’affirmation “il y aura une bataille navale demain”, la première et troisième phrase se traduisent par la même formule, $\Box(P\lor\neg P)$, alors que la deuxième phrase se traduit par $\neg\Box P\land\neg\Box\neg P$.
Le modèle ci-dessous représente les deux mondes possibles (avec ou sans bataille navale). Les deux formules sont vérifiées en chacun des mondes.
La logique modale “moderne” a elle aussi d’abord été aléthique lorsqu’elle née du désir de C.I. Lewis, en 1913, de renforcer l’implication matérielle $P\rightarrow Q$. Il a voulu lui substituer une implication stricte qui s’avérera finalement une implication matérielle renforcée du caractère de la nécessité. L’étude de l’implication stricte revenait donc à celle de la logique aléthique. La logique modale s’est ensuite développée de manière purement axiomatique jusqu’au début des années 60, quand S. Kripke introduit l’idée des mondes possibles pour créer une sémantique à la logique modale.
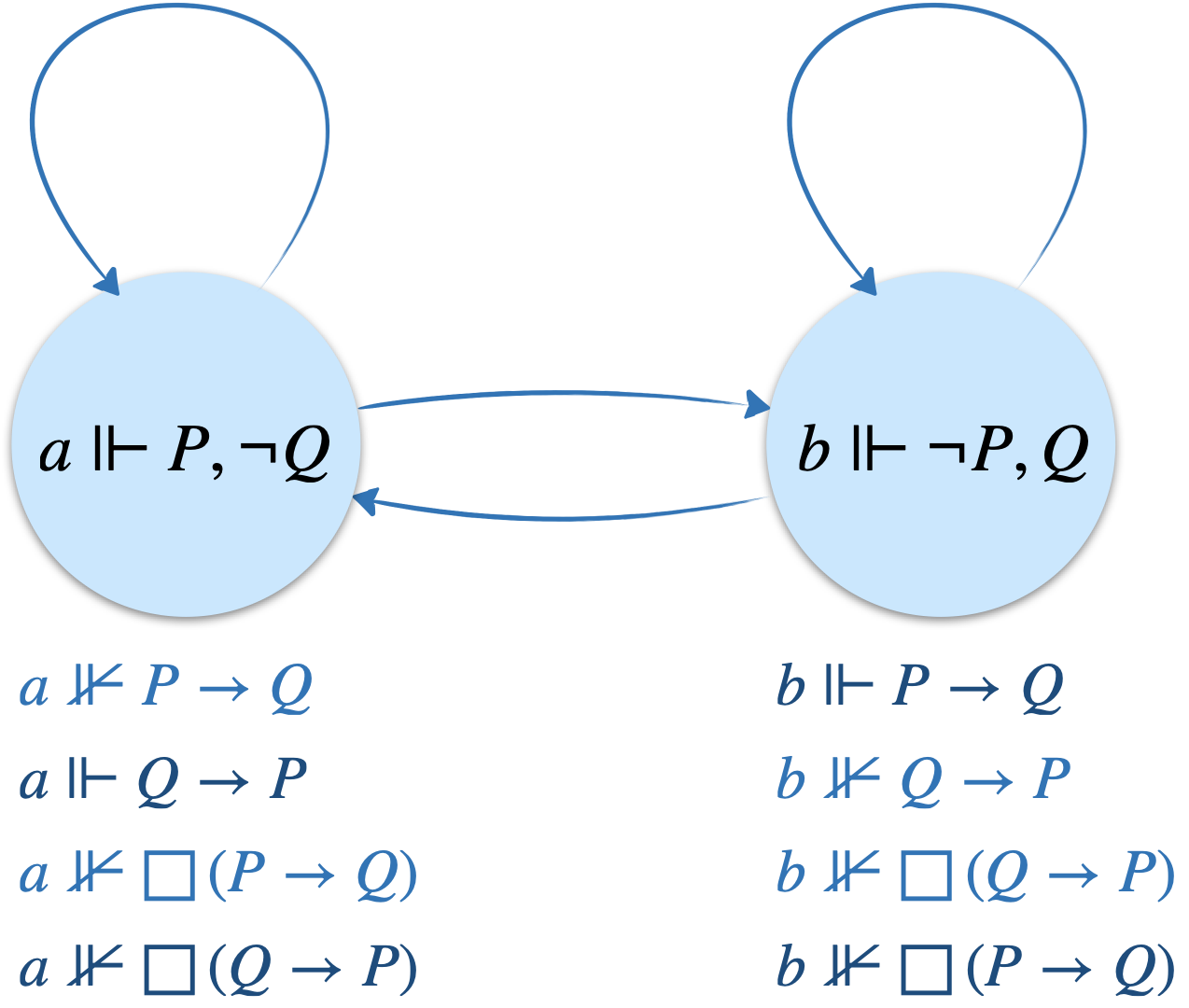
Mais revenons à l’implication. La formule $(P\rightarrow Q)\lor(Q\rightarrow P)$ est une tautologie du calcul des propositions. Pour deux propositions quelconques, il y en a donc toujours une qui implique l’autre, ce qui paraît absurde puisque les propositions peuvent être totalement indépendantes !
Avec l’implication stricte (implication ordinaire renforcée de la nécessité), le paradoxe disparaît car $\Box(P\rightarrow Q)\lor\Box(Q\rightarrow P)$ n’est pas valide. En effet, aucun des mondes du modèle ci-dessous ne satisfait la formule.
Le métaphysicien Charles Hartshorne a produit une “preuve” de l’existence de Dieu qui repose sur la logique $\textbf{{KB}}$ et qui nécessite un théorème de la logique modale $\vdash_\textbf{K} \Box(P\rightarrow Q)\rightarrow(\Diamond P\rightarrow\Diamond Q)$, l’axiome d’Anselme $G\rightarrow\Box G$ (si Dieu existe, il est nécessaire que Dieu existe) et l’axiome de Leibniz $\Diamond G$ (il est possible que Dieu existe).

Logique déontique
Cette logique porte sur l’obligation ou la permission.

Les deux principes de la logique aléthique (les deux axiomes choisis) deviennent clairement faux en logique déontique :
- $\Box P\rightarrow P$ : si $P$ est obligatoire, alors $P$ est vraie. Ça n'a ici pas de sens puisque c'est le caractère propre de l'obligation que de pouvoir être transgressée ! Il ne s'agirait pas sinon d'une obligation mais bien d'une nécessité.
- $P\rightarrow \Box\Diamond P$ : si $P$ est vraie, alors $P$ doit être permise. C'est à nouveau dénué de sens puisque des choses non permises arrivent. Considérer la propositions vraies revient d'ailleurs à tomber dans le sophisme naturaliste qui stipule que tout ce qui est naturel est bon ("il n'y a pas de vêtements dans la nature, donc il ne faut pas autoriser les vêtements").
Mais quelle formule s’adapte à la logique déontique ? L’axiome $\text{(D)}=\Box P\rightarrow\Diamond P$ affirmant que “si quelque chose est obligatoire, alors elle est permise”, convient naturellement. En triturant un peu la formule, on obtient $\Box P\rightarrow\Diamond P\equiv\neg\Box P\lor\Diamond P\equiv\Diamond\neg P\lor\Diamond P$ “soit c’est permis de faire une chose, soit c’est permis de ne pas la faire”. Ou encore : $\Diamond\neg P\lor\Diamond P\equiv \neg\Box P\lor\neg\Box\neg P\equiv\neg (\Box P\land\Box\neg P)$ “ne peuvent être obligatoire à la fois une chose et son contraire”. Tout cela semble plutôt évident.
Le système formel correspondant est donc $\textbf{KD}$ et la classe de systèmes de transition associée est $\mathscr{C}_{n.b.d.}$. La raison de cette topologie ouverte, avec des mondes qui ont tous un échappatoire est qu’une impasse est par construction un monde ou rien n’est permis !

Plusieurs paradoxes découlent de cette formalisation de l’obligation et de la permission. Penchons-nous d’abord sur le paradoxe de Ross (dû à… Ross).
L’énoncé “Il est obligatoire de poster la lettre” ($\Box P$ où $P$ correspond à poster la lettre) entraîne “il est obligatoire de poster la lettre ou de la brûler” ($\Box(P\lor B)$ où $B$ correspond à brûler la lettre). En effet $\Box P\rightarrow \Box(P\lor B)$ est prouvable sans hypothèse et est donc vérifiée en tout nœud de tout modèle de Kripke d’une logique modale normale (puisque l’axiome $\text{(D)}$ n’est même pas nécessaire à la preuve).
On part de la tautologie $P\rightarrow (P\lor Q)$ et de l’axiome $\text{(K)}$ :
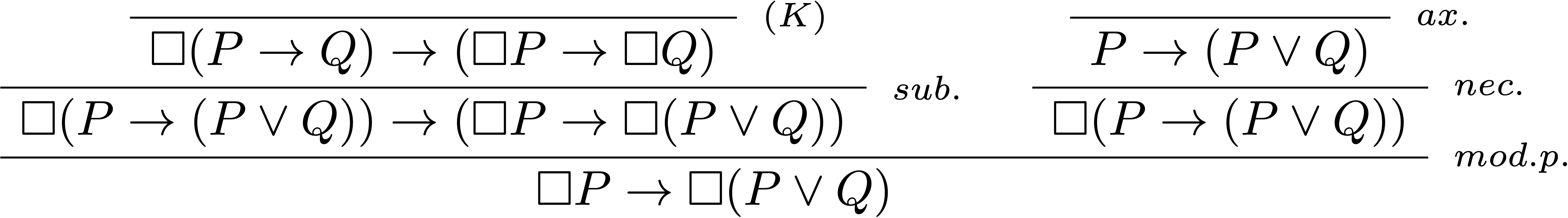
Si l’obligation de poster une lettre implique l’obligation de la poster ou de la brûler, alors on peut satisfaire l’obligation découlant de la première en brûlant la lettre. Certes, la lettre est loin d’être postée et on a d’ailleurs probablement enfreint un interdit, mais on a pourtant bien aussi satisfait une obligation…
L’implication a permis une sorte de réduction du poids de l’obligation par affaiblissement de $P$ en $P\lor B$.
On rencontre un autre problème en affaiblissant une conjonction comme le montre le paradoxe du Bon Samaritain (dû à Prior) : l’énoncé “il est obligatoire qu’Alice aide Bob qui a été volé” peut se traduire par $\Box(A\land B)$ où $A$ est “Alice aide Bob” et $B$ est “Bob a été volé”. Le problème est que $\Box(A\land B)\rightarrow\Box B$ est prouvable dans le système $\textbf{K}$ ($\text{(D)}$ n’est toujours pas nécessaire à la preuve).
On part de la tautologie $(A\land B)\rightarrow B$ et de l’axiome $\text{(K)}$ :
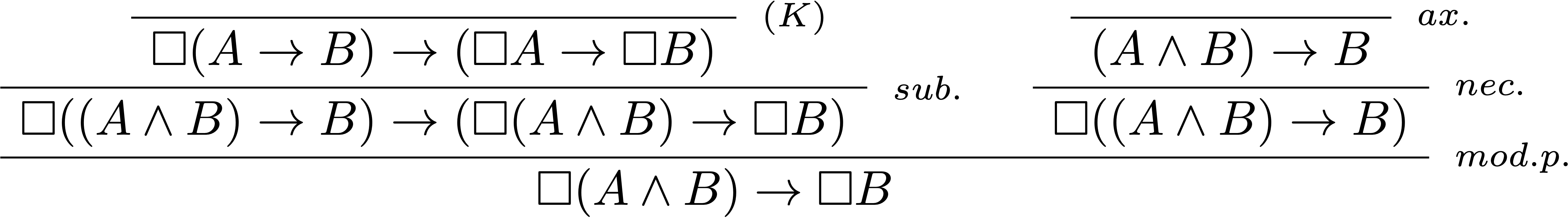
Donc si aider Bob lors d’un vol est obligatoire, il devient alors tout aussi obligatoire que Bob soit volé. Bob n’est pas ravi de la situation.

Une façon de se sortir de ces pièges est de maintenir une séparation stricte entre les descriptions des faits et les prescriptions déontiques. Cela évite d’inférer des faits (comme l’existence d’une victime) à partir des obligations morales ou légales.
Mais plus fondamentalement, en habillant modalement les deux tautologies ($P\rightarrow(P\lor Q)$ et $(A\land B\rightarrow B$) qui ont servi d’axiome dans les démonstrations, on permet de les interpréter sous un jour plus concret révélant leur bizarrerie. Le ver était dans le fruit dès l’utilisation de l’implication matérielle classique (celle que Lewis cherchait justement à dompter avec la modalité).
Pourquoi ces paradoxes sont-ils attachés à la logique déontique alors qu’on peut très bien obtenir les mêmes formules dans les autres logiques modales (puisqu’aucun axiome n’est nécessaire) ?
La logique déontique vise à proposer un guide éthique, des normes à suivre, là où la logique aléthique, par exemple, n’énonce qu’un état de fait. Devant l’affirmation que la nécessité du postage d’une lettre rend nécessaire son postage ou sa destruction par le feu, on a moins envie de monter au rideau (même si ça reste un peu bizarre). Une chose nécessaire s’impose physiquement et non moralement, il n’y a pas le choix, et l’application brute de la logique “mathématique” fait donc plus sens. En tant que prescripteur de comportement, la logique déontique a besoin d’une plus grande incarnation et de plus d’attention sur l’interprétation.

Le dilemme du libre choix (aussi dû à Ross) est une autre curiosité qui voit une hypothèse d’allure bénigne se transformer en boîte de Pandore.
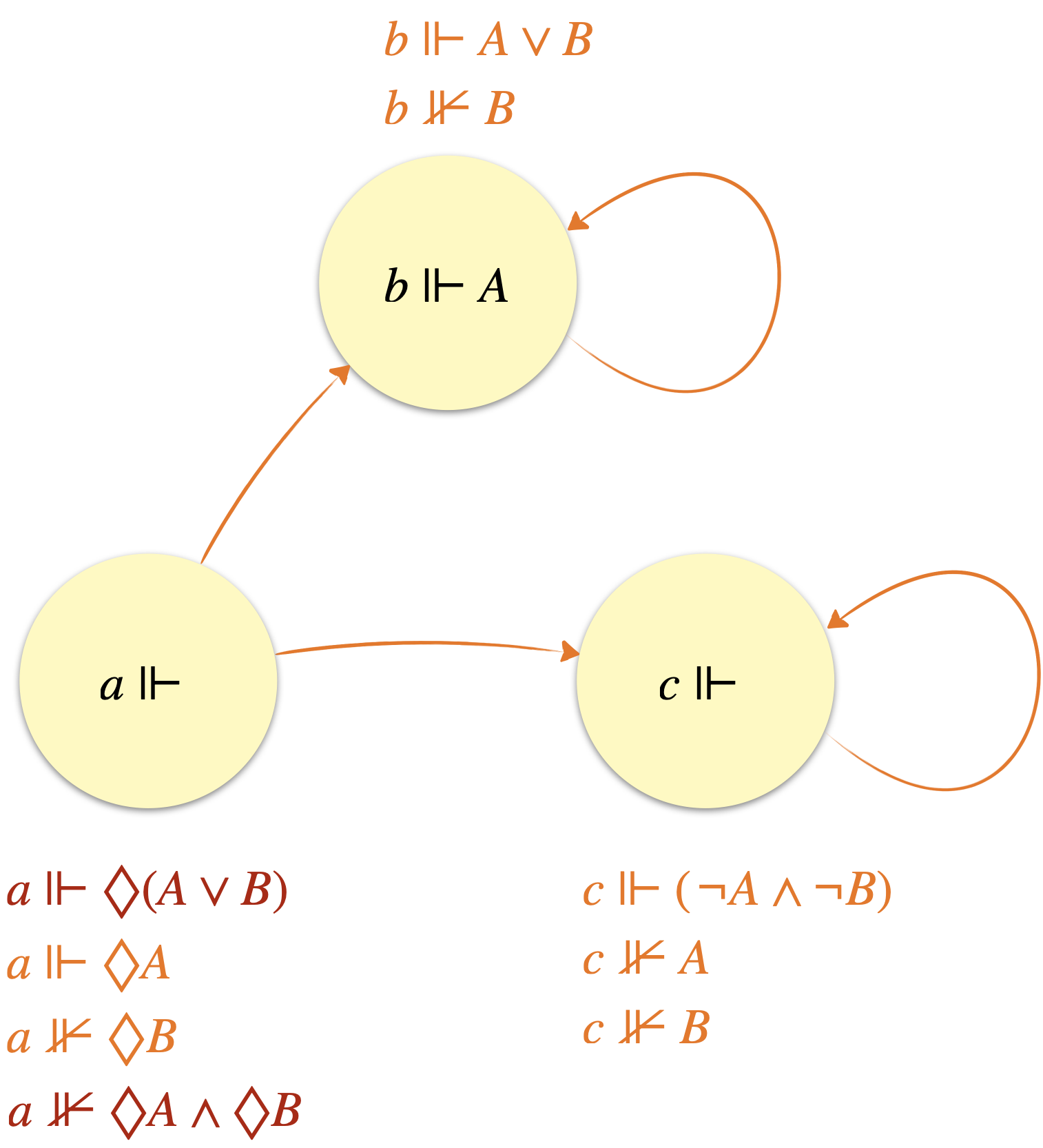
“Tu peux soit dormir sur le sofa soit dans la chambre d’amis” semble impliquer que “tu peux dormir sur le sofa et tu peux dormir dans la chambre d’amis”. On imagine ainsi que l’implication $\Diamond(A\lor B)\rightarrow(\Diamond A\land\Diamond B)$ est prouvable dans le système. Mais ce n’est pas le cas (voir ci-dessous). Qu’à cela ne tienne ! Ajoutons-là aux hypothèses. Cela serait dommage de se passer d’une implication si naturelle… Mais là, patatras, tout devient possible ! Imaginons en effet qu’il existe une quelconque possibilité $\Diamond A$, alors $\Diamond (A\lor B)$ aussi est vraie, et ce quel que soit $B$ (s’il ya un monde accessible où $A$ est vraie, alors dans ce même monde, $A\lor B$ est vraie) et grâce à notre pernicieux nouvel axiome, on déduit la vérité de $\Diamond A\land\Diamond B$ qui se réduit à celle de $\Diamond B$ (puisque par hypothèse $\Diamond A$ est vraie). On a finalement $\Diamond A\rightarrow \Diamond B$ pour tout $B$. La possibilité de $A$ rend tout possible grâce à cet axiome diabolique.
On prouve que $\Diamond(A\lor B)\rightarrow(\Diamond A\land\Diamond B)$ n’est pas prouvable dans le système $\textbf{KD}$ en trouvant un modèle appartenant à $\mathscr{C}_{n.b.d.}$ et tel qu’au moins un de ses nœuds ne satisfait pas la formule.
Un dernier pour la route : le dilemme de Sartre (dû à Lemmon). Il décrit l’impossibilité de représenter un conflit d’obligations en logique déontique standard (à cause de l’axiome $\text{(D)}$). La situation dans laquelle se retrouve Jephté dans la Bible en est une illustration parfaite. Jephté promet à Dieu de sacrifier le premier être vivant qu’il croise s’il gagne la guerre. Il gagne la guerre et croise sa fille (c’est ballot). On a bien conflit d’obligations puisque l’obligation de ne pas tuer sa fille doit bien figurer quelque part aussi… On a donc une situation où il est obligatoire de faire une chose $\Box A$ et aussi obligatoire de ne pas la faire $\Box \neg A$. Or $\Box A\rightarrow \Diamond A$ d’après $\text{(D)}$ et par dualité, on obtient $\Box A\rightarrow \neg \Box\neg A$. La situation de départ (la satisfaction de $\Box A$ et $\neg\Box A$), bien qu’envisageable, aboutit à une inconsistance interdisant donc même son existence dans le système formel $\textbf{KD}$ (qui commet sûrement là un pécher).
Malgré ses “petits” défauts, la logique déontique connait différentes applications en informatique. En autorisant l’expression de raisonnements normatifs, elle permet de spécifier la marche à suivre en cas de comportement anormal. De manière plus général, elle propose un cadre pour gérer les autorisations et politiques d’accès, et on la retrouve dans le secteur de l’automatisation juridique ou encore celui des contraintes sur les bases de données.
Logique épistémique
Elle permet de raisonner à propos de la connaissance d’un ou plusieurs agents.
C’est elle qui est au cœur de notre histoire introductive de dragons ou de cette blague sur des logiciens assoiffés.

Appelons $1$, $2$ et $3$ les trois logiciens de gauche à droite et $B_i$ l'affirmation "le logicien $i$ veut une bière".
- Au départ, $1$ veut une bière (et elle le sait…), mais elle ne peut pas savoir dans lequel des 4 mondes restant possibles elle se trouve : $[1]B_1\land\langle1\rangle B_2\land\langle1\rangle B_3$. Comme le monde où $B_1\land B_2\land B_3$ fait partie des mondes possibles, elle répond “je ne sais pas”.
- $2$ en déduit $B_1$. Car si $\neg B_1$, alors $[1]\neg B_1$ et donc le monde $B_1\land B_2\land B_3$ où tous veulent picoler n’est plus accessible et elle aurait répondu non. Voulant elle aussi une bière, $2$ hésite encore entre deux mondes $[2]B_1\land[2]B_2\land\langle2\rangle B_3$.
- $3$ en déduit $B_2$ et peut maintenant répondre puisque $[3]B_1\land[3]B_2\land[3] B_3$ ($3$ aussi veut une bière bien sûr). Plus qu’un monde possible, celui qui satisfait $B_1\land B_2\land B_3$. C’est un grand “Oui !”.
La règle de nécessitation associée à l’axiome $\text{(K)}$ (valables dans tout nœud de tout système d’une logique normale) impliquent l’omniscience logique de l’agent $i$. En effet, par nécessitation $A\rightarrow B$ devient $[i](A\rightarrow B)$ et $\text{(K)}=[i](A\rightarrow B)\rightarrow([i]A\rightarrow [i]B)$. Par conséquent, l’agent connait toutes les conséquences logique ($[i]B$) de ce qu’il sait ($[i]A$).
En logique modale épistémique, la relation binaire entre deux mondes est une relation d’indistinguabilité ; l’agent ne sait pas dans quel monde il se trouve. Cette relation est nécessairement symétrique par la notion même d’indistinguabilité. Et comme un monde ne pourra jamais être distingué de lui-même, il faut ajouter une relation réflexive de chaque monde à lui-même. Le dernier ingrédient est la transitivité. Si $a$ est indistinguable de $b$ et que $b$ est indistinguable de $c$, alors $a$ est aussi indistinguable de $c$. Une telle relation, symétrique, réflexive et transitive est une relation d’équivalence. Et on aurait pu partir de là finalement puisque c’est bien l’équivalence qui se cache derrière la notion d’indistinguabilité.
La classe de systèmes de transition assurant une relation d’équivalence entre les mondes possibles correspond à la logique $\textbf{S5}$.
Deux jeux d’axiomes équivalents permettent d’obtenir $\textbf{S5}$ : $\set{(\text{K}),(\text{T}),(\text{B}),(\text{4})}$ où $\text{(T)}$ apporte la réflexivité, $\text{(B)}$ la symétrie et $\text{(4)}$ la transitivité, ou bien le jeu $\set{(\text{K}),(\text{T}),(\text{5})}$ où $\text{(5)}$ apporte l’euclidanité sachant qu’un système de transition euclidien est à la fois symétrique et transitif.
Les axiomes doivent être vérifiés dans tous les mondes possibles. Ainsi $\text{(T)}=[i]P\rightarrow P$ signifie que dans un monde quelconque, si l’agent $i$ sait que $P$, alors $P$ est vrai dans ce monde (l’agent ne sait que des choses vraies). Et il faut aussi que soit réalisée $\text{(5)}=\neg[i]P\rightarrow[i]\neg[i]P$, ce qui signifie que si l’agent $i$ ne sait pas quelque chose, alors il sait qu’il ne le sait pas. C’est le principe d’introspection négative.
L’agent de la logique $\textbf{S5}$ est une sorte d’agent idéal pour lequel l’accès à la connaissance est maximal (sans qu’il ne sache tout pour autant). Il n’est tellement pas humain qu’il ne peut pas croire
On place parfois l’agent dans une logique inférieure, $\textbf{S4}$, qui perd la symétrie (et donc l’indistinguabilité !). L’introspection négative disparaît alors et est remplacée par l’introspection positive $\text{(4)}:[i]P\rightarrow [i][i] P$ où si l’agent sait quelque chose, alors il sait qu’il sait. Mine de rien, ça lui limite pas mal l’accès à la connaissance par rapport à l’autre introspection. L’agent reste idéal en ce qu’il conserve une omniscience logique totale, mais il peut vivre dans un monde ou il peut croire possible qu’il sait quelque chose qu’il ne sait pas (la honte).
Dans $\textbf{S4}$, l’accessibilité n’est plus nécessairement réciproque entre les mondes. Cela introduit une hiérarchie, un ordre où certains mondes peuvent être considérés comme des extensions ou des raffinements d’autres, des mondes “plus informés”. C’est pertinent pour modéliser la communication dans des réseau où l’information n’est pas toujours réciproquement échangée (dès que les canaux sont asymétriques comme c’est le cas dans la plupart des structures hiérarchiques).
Couplé à une logique temporelle, cela permet de modéliser un apprentissage progressif où l’acquisition d’information se fait de manière séquentielle ou cumulative. En robotique ou en intelligence artificielle, cela permet dans la même veine de modéliser des processus de planification où chaque décision ou action mène à un nouvel état du monde qui intègre toutes les connaissances et conséquences des actions précédentes.
Logique temporelle
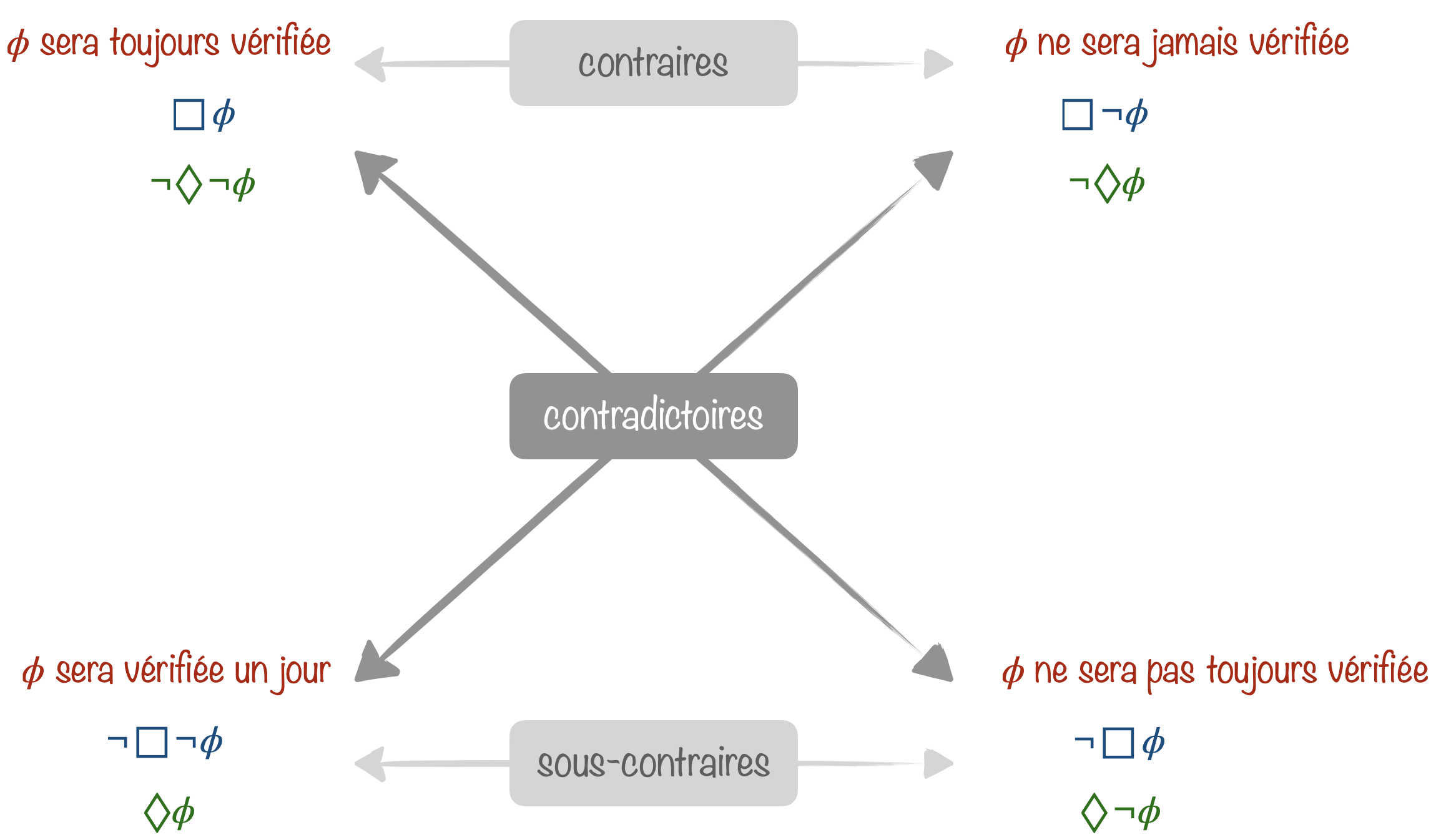
Il y a beaucoup de logiques temporelles qui multiplient généralement les opérateurs modaux. Mais de base, une logique modale temporelle peut exprimer ce qu’on trouve dans le carré des oppositions ci-dessous.
La logique temporale peut aussi bien s’intéresser au passé qu’au futur.
Le temps dont il est question ici est discret, chaque monde possible correspondant à un instant $t$.
Pas de raison particulière pour que la relation d’accessibilité entre ces mondes soit réflexive ou symétrique, par contre, elle se doit d’être transitive pour conserver l’ordonnancement entre les différents instants considérés. L’axiome clé est donc le $\text{(4)}$ et le futur d’un monde correspond alors à l’ensemble des mondes qui lui sont accessibles (l’absence de réflexivité entraîne que le monde actuel ne fasse pas partie du futur).
On peut alors traduire les opérateurs modaux par :
- $\Box \phi$ : $\phi$ sera toujours vérifiée,
- $\Diamond \phi$ : $\phi$ sera vérifiée à un certain moment.
Cela permet d'exprimer des énoncés tels que :
- $\Box\neg(\texttt{started}\land\neg\texttt{ready})$ : il est impossible d’atteindre un état où $\texttt{started}$ est activé, mais pas $\texttt{ready}$,
- $\Box(\texttt{request}\rightarrow\Diamond\texttt{acknowledged})$ : pour tout état, si une demande (de quelque ressource que ce soit) est effectuée, alors elle sera finalement reconnue,
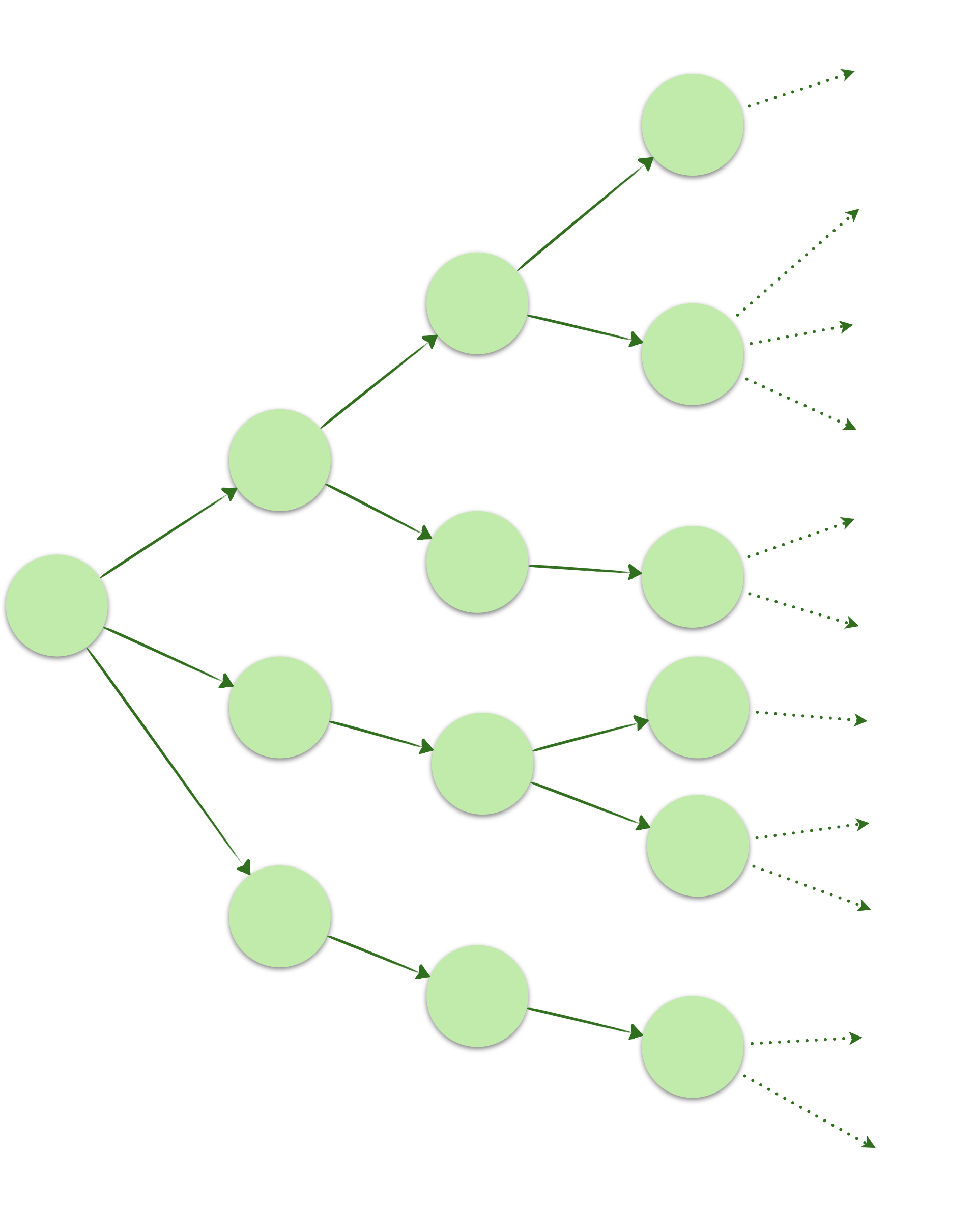
Le temps des logique temporelles peut prendre une forme linéaire ou arborescente.
Dans la logique temporelle linéaire (LTL), les instants s’enchaînent en un collier de perles infini. C’est idéal pour explorer un système déterministe ou une seule branche d’exécution et vérifier efficacement que toutes les spécifications sont satisfaites.

Dans une logique temporelle arborescente (CTL), le champ des possibles s’ouvrent. Elle permet de modéliser des systèmes non déterministes ou des choix amenant sur des branches différentes peuvent être faits.
La logique temporelle est très utilisée en vérification formelle, où la technique de base est essentiellement le model checking.
Logique de la prouvabilité
Souhaitant éprouver la stabilité de l’édifice mathématique, en particulier l’arithmétique (la science des nombres, le cœur des maths), Gödel a imaginé une méthode astucieuse, une sorte de hack qui lui permit de plonger les énoncés logiques dans le champ de l’arithmétique (en particulier sur l’Arithmétique de Peano $\text{PA}$, une théorie - ensemble d’axiomes - en logique du premier ordre dont l’arithmétique des entiers est un modèle). En associant à chaque formule un numéro (le numéro de Gödel ou code de Gödel), noté $\ulcorner\phi\urcorner$, il a permis aux nombres de parler d’eux-mêmes dans une sorte d’épanchement introspectif.
Ce qui semblait à l’époque un processus éminemment complexe est devenu trivial à l’ère de l’informatique. Pour associer un nombre unique à une formule, il suffit par exemple de regarder le code binaire du fichier de traitement de texte où la formule est écrite (et d’ajouter éventuellement un “1” au début si ça commence par des “0”).
On peut même coder sans problème un arbre de preuve complet (tout ce qu’on peut écrire dans un traitement de texte finalement). Dès lors, une formule peut très bien parler du fait qu’une autre formule est démontrable puisqu’il s’agit de dire qu’il existe un entier possédant les propriétés qui le caractérisent comme étant le code d’une preuve de cette formule. C’est ce que fait la formule $\Box\phi$ où l’opérateur de modalité $\Box$ prend alors le sens de “est prouvable” (elle équivaut à la fameuse formule de Gödel $G\leftrightarrow\neg\text{Bew}(\ulcorner G\urcorner)$, $\Box$ correspondant à $\text{Bew}(x)$, “bew” étant le début du mot allemand beweisbar qui signifie prouvable).

Le premier théorème d’incomplétude de Gödel s’appuie sur une formule affirmant sa propre non prouvabilité $\neg\Box\phi\leftrightarrow \phi$. Si on peut démontrer la formule $\neg\Box\phi\leftrightarrow \phi$ dans un système donné, alors on prouve qu’il existe une formule non démontrable et pourtant vraie, ce qui impose l’incomplétude du système.
Lemme de diagonalisation :
Pour toute formule arithmétique $f(x)$, il existe une formule arithmétique $P$ telle que $P\leftrightarrow f(P)$.
C’est l’outil permettant à Gödel de construire des formules autoréférentes comme $\neg\Box\phi\leftrightarrow \phi$.
Le lemme dit que pour toute formule $\phi$, il existe une formule $S(\ulcorner\phi\urcorner)$ qui parle de $\phi$ (une formule méta en somme) telle qu’on peut prouver $\phi$ si et seulement si on peut prouver $S(\ulcorner\phi\urcorner)$ : $\vdash\phi\leftrightarrow S(\ulcorner\phi\urcorner)$.
Pour démontrer le lemme, on va supposer que $n$ est le numéro d’une formule de la forme $A(x)$ où $x$ est une variable et on définit $F(n)=\ulcorner A(\ulcorner A(x)\urcorner)\urcorner$ et si $n$ ne correspond pas à une formule sous cette forme, alors $F(n)=0$.
Notons que $F$ dépend du choix de la variable $x$. Ainsi, $F(\ulcorner y=0 \urcorner)=\ulcorner(\ulcorner y=0 \urcorner) = 0\urcorner$ et $F(\ulcorner x=0 \urcorner)=\ulcorner(\ulcorner x=0 \urcorner) = 0\urcorner$.
Soit $g(w)\equiv S(F(w))$ et $\phi\equiv g(\ulcorner g(x)\urcorner)$.
On obtient :
$$ \begin{aligned} \phi &= g(\ulcorner g(x)\urcorner)\\ &= S(F(\ulcorner g(x)\urcorner) \\ &= S(\ulcorner g(\ulcorner g(x)\urcorner)\urcorner)\\ &= S(\ulcorner\phi\urcorner) \end{aligned} $$
Très informellement, le lemme de diagonalisation exprime l’échec de l’argument de la diagonale de Cantor pour construire une formule $S(x)$ qui ne ferait pas partie de l’ensemble dénombrable des formules prouvables. La clôture de l’ensemble des formules prouvables par action d’une formule sur les éléments de cet ensemble empêche en effet de “diagonaliser à l’extérieur” du domaine.
La formule autoréférente de Gödel est proche du fameux paradoxe du menteur “cette phrase est fausse”.
Premier théorème d’incomplétude :
Dans un système formel consistant (= cohérent = système dans lequel on ne peut pas prouver le faux) suffisamment expressif pour décrire l’arithmétique, on ne peut pas prouver toutes les formules vraies (comme la formule qui affirme sa non prouvabilité). La prouvabilité est plus faible que la vérité.
Montrons dans la logique $\textbf{K4}$ que $\vdash\phi\leftrightarrow\neg\Box\phi$ permet d’arriver à $\vdash\neg\Box\bot\rightarrow\neg\Box\phi$ ; la formule n’est pas prouvable si aucune contradiction n’est prouvable. On obtient donc bien l’essence du premier théorème d’incomplétude.
- $\phi\leftrightarrow\neg\Box\phi$
- $\Box\phi\rightarrow\neg\phi$ (à partir de 1.)
- $\Box(\Box\phi\rightarrow\neg\phi)$ (nécessitation)
- $\Box\Box\phi\rightarrow\Box\neg\phi$ (distribution de la boite grâce à $\text{(K)}$)
- $\Box\phi\rightarrow\Box\neg\phi$ (par l'axiome $\text{(4)}= \Box \phi\rightarrow\Box\Box\phi$ et avec l'étape 4., on déduit $\Box\phi\rightarrow\Box\Box\phi\rightarrow\Box\neg\phi$)
- $\Box\phi\rightarrow\Box\phi\land\Box\neg\phi$ (à partir de 5. et $\Box\phi\rightarrow\Box\phi$)
- $\Box\phi\rightarrow\Box(\phi\land \neg\phi)$
- $\Box\phi\rightarrow\Box\bot$
- $\neg\Box\bot\rightarrow \neg\Box\phi$ (contraposée de 8.)
Le théorème de Löb utilise un autre formule autoréférente, $\Box(\Box\phi\rightarrow\phi)\rightarrow\Box\phi$, s’apparentant plutôt, dans son cas, au paradoxe d’un diseur de vérité “ce que je dis là est vrai” (aucune valeur de vérité ne semble applicable puisqu’un menteur dirait la même chose).
Et la surprise est que de tels points fixes sont prouvables et par conséquent vrais.
Le théorème de Löb stipule que les formules dont on peut prouver que $\Box\phi\rightarrow\phi$ sont les formules prouvables :
Le théorème affirme donc que si on peut prouver une formule en admettant comme axiome qu’on peut la prouver, alors on peut la prouver sans l’axiome. Le théorème est donc une sorte de méthode Coué logique, une prophétie autoréalisatrice ; “si tu crois en toi, ça va le faire”. C’est bizarre, mais ça se démontre.
Preuve du théorème de Löb :
On suppose $\vdash \Box\phi\rightarrow\phi$.
Grâce au lemme de diagonalisation, on construit la formule arithmétique autoréférente suivante :
$\vdash\sigma\leftrightarrow (\Box\sigma\rightarrow\phi)$ ("ma propre prouvabilité implique $\phi$").
- $\vdash\Box(\sigma\rightarrow (\Box\sigma\rightarrow\phi))$ (par nécessitation)
- $\vdash\Box\sigma\rightarrow \Box(\Box\sigma\rightarrow\phi)$ puis $\vdash\Box\sigma\rightarrow (\Box\Box\sigma\rightarrow\Box\phi)$ (distribution de la boite grâce à $\text{(K)}$)
- On a donc $\vdash \Box\sigma\rightarrow\Box\Box\sigma$ et $\vdash \Box\sigma\rightarrow\Box\phi$
- $\vdash \Box\sigma\rightarrow\phi$ (car $\vdash \Box\sigma\rightarrow\Box\phi\rightarrow\phi$ puisqu'on suppose $\vdash \Box\phi\rightarrow\phi$)
- $\vdash (\Box\sigma\rightarrow\phi)\rightarrow\sigma$ (sens réciproque de la formule autoréférente)
- $\vdash\sigma$ par modus ponens de 4. et 5.
- $\vdash\Box\sigma$ par nécessitation.
- $\vdash \phi$ par modus ponens de 4. et 7.
Si un système formel est consistant alors il ne peut pas prouver sa propre consistance. Et donc les seuls systèmes qui peuvent prouver leur consistance sont ceux qui sont inconsistants…
C’est le second théorème d’incomplétude de Gödel.
Ce théorème n’est autre que la contraposée du théorème de Löb !
Avec $\phi=\bot$, on obtient :
si $\vdash\neg\Box\bot$, alors $\vdash\neg\Box(\Box\bot\rightarrow\bot)$ et comme $\Box\bot\rightarrow\bot\equiv\neg\Box\bot\lor\bot\equiv\neg\Box\bot$, on a finalement si $\vdash\neg\Box\bot$, alors $\vdash\neg\Box(\neg\Box\bot)$
Par dualité, $\Diamond P = \neg\Box\neg P$. Donc $\Diamond P$ exprime qu’on ne peut pas prouver que $P$ est faux. Autrement dit, $\Diamond P$ affirme que $P$ est consistant (cohérent) dans le système formel.
$\neg\Box\bot\rightarrow\neg\Box(\neg\Box\bot)$ devient alors $\Diamond\top\rightarrow \neg\Box(\Diamond \top)$ (“si une théorie est consistante, alors on ne peut pas prouver que la théorie est consistante”).
La logique de la prouvabilité de Gödel-Löb ($\textbf{GL}$) est formée à partir du système $\textbf{K}$ auquel on ajoute l’axiome de Löb $\text{(L)}=\Box(\Box\phi\rightarrow\phi)\rightarrow\Box\phi$ (c’est la version formalisée du théorème de Löb).
$\vdash_\textbf{GL}\text{(4)}=\Box\phi\rightarrow\Box\Box \phi$
Et donc $\textbf{K4}≤\textbf{KL}$ ($\textbf{K4}$ se réduit à $\textbf{KL}$).
Obtention d’un premier théorème : $\vdash_\textbf{K}\Box P\rightarrow \Box ((\Box P\land \Box\Box P)\rightarrow(P\land \Box P))$
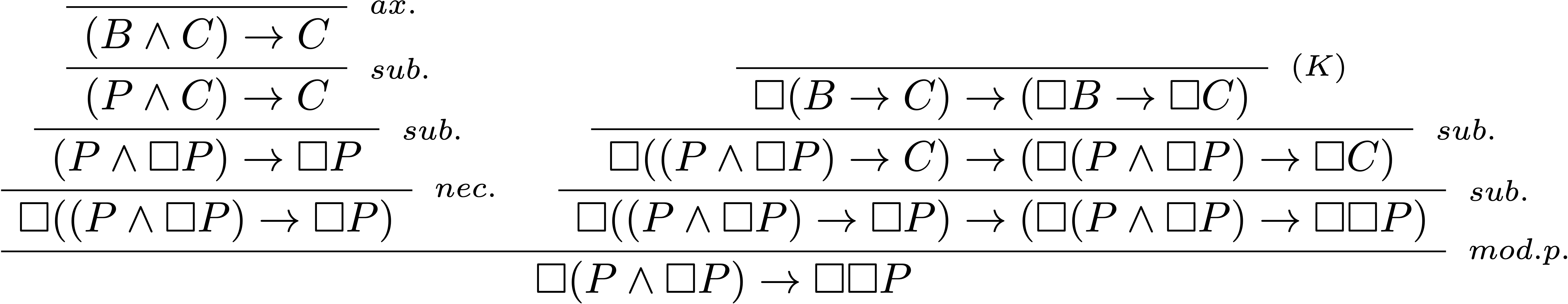
La classe des systèmes de transition qui valide $\textbf{GL}$ est donc transitive !
Montrons de plus que cette classe est irréflexive et asymétrique.
Il suffit de trouver un modèle qui valide $\color{#1DB100}\text{(L)}$ sans valider ni $\color{#FF42A1}\text{(B)}=\Box P\rightarrow \Diamond\Box P$, ni $\color{#F27200}\text{(T)}=\Box P \rightarrow P$.
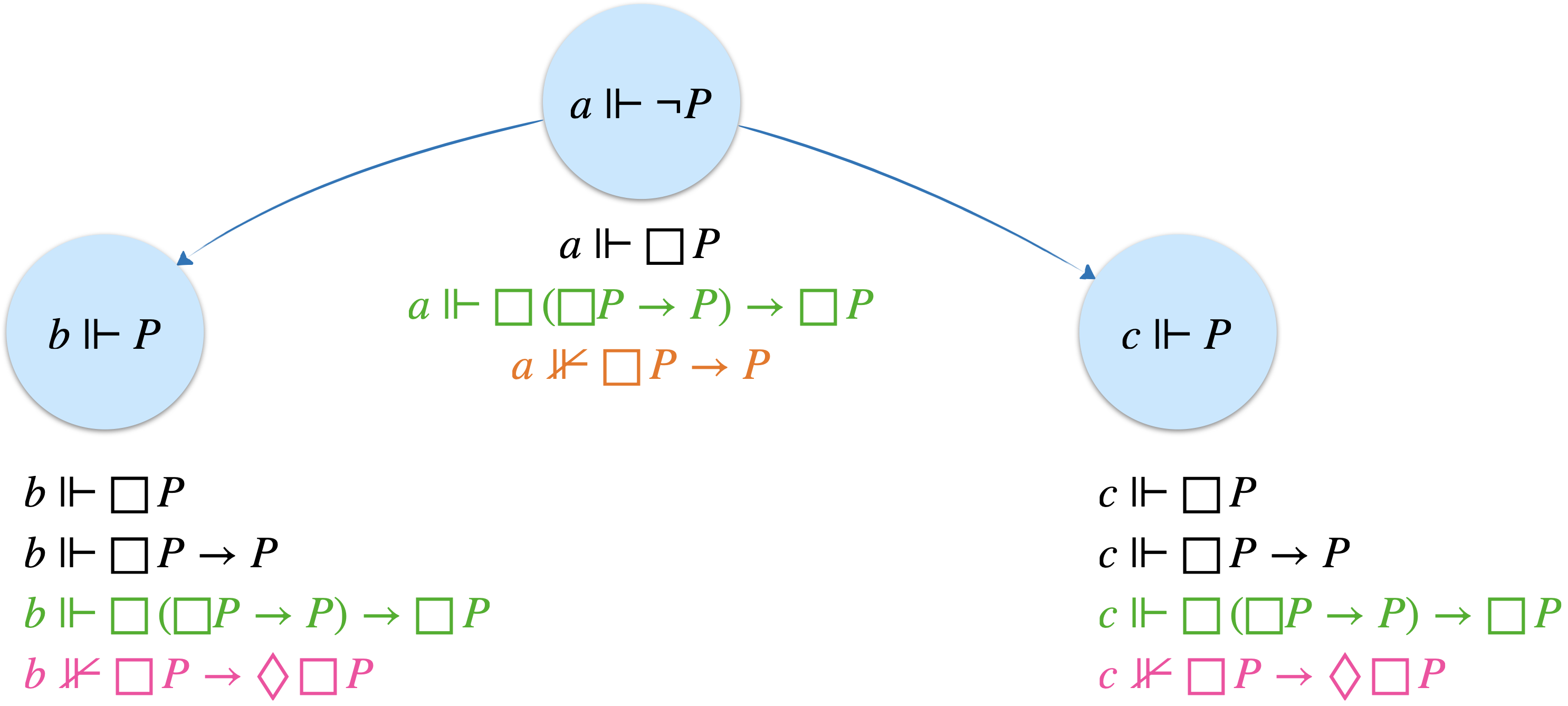
Or un graphe transitif et non réflexif, ni symétrique n’est autre qu’un arbre. On va aller un peu plus loin en montrant que ces arbres doivent être en plus finis. Et c’est plutôt génial que cette logique de la prouvabilité s’exprime naturellement sur des arbres finis qui représentent intuitivement la notion de preuve (la racine représentant la formule prouvée, et les feuilles les axiomes).
La logique $\textbf{GL}$ est correcte et complète par rapport à la classe $\mathscr{C}_{\text{arbres finis}}$ des modèles de Kripke à la fois transitifs, irréflexifs, asymétriques et bornés à droite (sans suite infinie de mondes).
Correction :
Si $ \vdash_\textbf{GL} \phi$, alors $\models_{\mathscr{C}_{\text{arbres finis}}}\phi$.
Comme $\text{(L)}$ est le seule axiome ajouté à $\textbf{K}$, il faut montrer que l’ensemble des systèmes de transition qui valide l’axiome de Löb est restreint aux seuls arbres finis (l’axiome $\text{(K)}$ est valide dans $\mathscr{C}$ et les règles de la logique modale normale conserve la validation).
Supposons que l’axiome ne soit pas satisfait en un nœud $a$ d’un arbre fini $\mathcal{T}=(N,A)$. On a donc $\langle \mathcal{T},a\rangle \not\models \Box(\Box P\rightarrow P)\rightarrow \Box P$.
Cela implique :
- $\langle \mathcal{T},a\rangle \models \Box(\Box P\rightarrow P)$, et
- $\langle \mathcal{T},a\rangle \not\models \Box P$.
Par contre, la première affirmation nous assure que $\langle \mathcal{T},a'\rangle \models \Box P\rightarrow P$.
Par conséquent $\langle \mathcal{T},a'\rangle \not\models \Box P$. Cela signifie qu'il existe un nœud $a''\in N$, successeur de $a'$ ($a'\longrightarrow a''$) tel que $\langle \mathcal{T},a''\rangle \not\models P$.
Par transitivité, $a \longrightarrow a''$. Or si on retourne à l'affirmation $1.$, on a aussi $\langle \mathcal{T},a''\rangle \models \Box P\rightarrow P$, ce qui va conduire de fil en aiguille à une séquence infinie de successeurs de $a$, contredisant ainsi que $\mathcal{T}$ soit fini.
On en conclut que l’axiome de Löb et donc $\textbf{KL}$ est valide dans tout arbre fini.
Complétude :
Si $\models_{\mathscr{C}_{\text{arbres finis}}}\phi$, alors $\vdash_\textbf{GL} \phi$.
Comme entrevu plus haut, l’opérateur de modalité peut s’interpréter comme la formule arithmétique de Gödel $\text{Bew}(x)$. Il s’agit plus précisément d’une formule de l’Arithmétique de Peano $\mathbf{PA}$. Il se trouve qu’on peut traduire toute formule de la logique modale dans $\textbf{PA}$ et on montre alors que tout théorème de $\textbf{GL}$ est prouvable dans $\textbf{PA}$. C’est ce qu’on peut appeler la correction arithmétique de $\textbf{GL}$. Et mieux, Solovay a prouvé aussi sa complétude arithmétique ; toute formule prouvable de l’arithmétique est un théorème de $\textbf{GL}$.