
Notes de lecture du livre La logique pas à pas de Jacques Duparc que je paraphrase allégrement.
Logique modale
Axiomatique : les systèmes logiques
Nous cherchons l’équivalent en logique modale des tautologies pour le calcul des propositions ; des formules vraies dans tous les modèles, ou plutôt dans toute une classe de modèles car comme on va le voir, la topologie d’un modèle contraint la vérité à l’intérieur de celui-ci.
La logique de la classe $\mathscr{C}$ est la classe de toutes les formules qui sont valides dans tous les systèmes de transition de $\mathscr{C}$ : $\mathbb{Log}_\mathscr{C}=\set{\phi|\text{pour tout }\mathcal{S}\in\mathscr{C},\mathcal{S}\Vdash^{\forall a,\forall \mathcal{V}} \phi}$
Cette logique doit contenir toutes les formules qui sont des tautologies du calcul des propositions puisque ces formule de profondeur modale nulle (pas d’opérateurs modaux) sont nécessairement forcées en tout nœud de n’importe quel modèle.
- Si la logique contient la formule $\phi$, elle doit aussi contenir $\Box\phi$. En effet, si $\phi$ est forcée en tout nœud, alors le successeur de tout nœud force aussi $\phi$. On appelle ça la nécessitation (ou généralisation) d'une formule.
- De plus, si $\phi$ appartient à la logique, la satisfaction de $\phi$ en un nœud $a$ donné est indépendante de la valuation $\mathcal{V}$ (que $P$ soit vraie ou fausse, $P$ est forcée au nœud $a$). Par conséquent, que $\psi$ soit vraie ou fausse, la satisfaction de la formule $\phi[\psi/P]$ ne varie pas. Toutes substitutions uniformes opérées sur les variables d'une formule appartenant à la logique sera aussi dans la logique.
- Enfin, la logique de la classe de tous les systèmes de transition est close par modus ponens ; si $\phi \rightarrow\psi$ et $\psi$ appartiennent toutes deux à la logique, alors $\psi$ également. En effet, le modus ponens préserve la validité puisque si un modèle vérifie en un noud à la fois $\psi$ et $\psi\rightarrow\phi$, alors (par définition de l'interprétation de l'implication) il vérifie également $\phi$.
Pour déterminer des nouvelles tautologies en calcul des propositions, on a utilisé des systèmes de déduction (à la Hilbert, déduction naturelle, calcul des séquents). La modalité complique un peu les choses et seul le système à la Hilbert va pouvoir s’adapter facilement.
- Un axiome est une formule.
- Un système formel est un ensemble d'axiomes.
Soient $I$ un ensemble non vide, $\phi$ une formule et $\textbf{S}$ un système formel.
Une preuve de la formule $\varphi$ dans le système formel $\textbf{S}$ est une suite finie de formule $\langle\varphi_1,\varphi_2,\ldots,\varphi_n\rangle$ telle que :
- $\varphi_n=\phi$
- chaque $\varphi_l$ vérifie l'une des quatre conditions suivantes :
- $\varphi_l \in \textbf{S}$ ($\varphi_l$ est un axiome)
- $\varphi_l$ est obtenue par application de la règle du modus ponens à deux formules d'indice inférieurs $\varphi_j$ et $\varphi_k$ où $j , k < l$ ($\varphi_j = \varphi_k\rightarrow\varphi_l$)
- $\varphi_l = \varphi_k[\theta /P]$ où $k < l$ (substitution d'une variable $P$ quelconque par une formule $\theta$ quelconque dans une formule d'indice inférieure)
- $\varphi_l = [i]\varphi_j$ où $j < l$ ($\varphi_l$ est obtenue à partir de l'application de la règle de nécessitation appliquée à une formule d'indice inférieure pour une étiquette $i\in I$ quelconque)
Exemple 1 :
Si $\textbf{S}$ désigne l’ensemble des tautologies du calcul des propositions, alors la suite
En effet :
- $\varphi_1=P\rightarrow(P\lor\neg P)$ est une tautologie du calcul des propositions et donc un axiome du système formel $\textbf{S}$,
- $\varphi_2 = \Diamond Q\rightarrow(\Diamond Q\rightarrow\lor\neg\Diamond Q) = P\rightarrow(P\lor\neg P)[\Diamond Q /P]$ est la substitution de la formule $\Diamond Q$ à $P$ dans $\varphi_0$,
- $\varphi_3 = \Box (\Diamond Q\rightarrow(\Diamond Q\rightarrow\lor\neg\Diamond Q))$ est obtenu par nécessitation de $\varphi_1$,
- $\varphi_4 = \Box (\Diamond \phi\rightarrow(\Diamond \phi\rightarrow\lor\neg\Diamond \phi) = \varphi_3[\phi/Q]$
C’est plus élégant de représenter l’enchaînement sous forme d’arbre :
Exemple 2 :
Si $\textbf{S}$ désigne l’ensemble des tautologies du calcul des propositions auquel on ajoute la formule $P\rightarrow\Diamond P$, alors l’arbre ci-dessous décrit une preuve de $\Box(\phi\rightarrow\Diamond\Diamond\phi)$ dans ce système :
Soient $\textbf{S}$ un système formel et $\Gamma$ un ensemble de formules appelées hypothèses.
On écrit $\Gamma\vdash_\textbf{S}\phi$ s’il existe un ensemble fini de formules $\set{\psi_1,\psi_2,\ldots,\psi_n}\subseteq\Gamma$ tel que la formule $(\psi_1\land\psi_2\land\ldots\land\psi_n)\rightarrow\phi$ puisse être prouvée dans le système formel $\textbf{S}$. Autrement dit le séquent $\vdash_\textbf{S}(\psi_1\land\psi_2\land\ldots\land\psi_n)\rightarrow\phi$ est vérifiée pour un nombre fini de formules bien choisies de $\Gamma$.
Attention, ici les hypothèses n’ont pas le même sens qu’en logique des propositions. En effet, pour prouver le séquent $\phi\vdash_\textbf{S}\psi$, on ne peut pas ajouter $\phi$ aux axiomes et tenter d’atteindre $\psi$ à partir des règles (modus ponens, substitution uniforme et nécessitation). Il faut ici réussir à prouver la formule $\phi\rightarrow\psi$ sur la base des seuls axiomes.
Si on pouvait faire comme en logique des propositions, prouver $\phi\vdash_\textbf{S}\Box\phi$ deviendrait évident : on place $\phi$ dans les axiomes et on applique la règle de nécessitation. Mais non, il faut pouvoir prouver $\vdash_\textbf{S}\phi\rightarrow\Box\phi$ et comme on va le voir, dans le système $\textbf{K}$, la formule $P\rightarrow\Box P$ n’est pas prouvable ($P\nvdash_\textbf{K}\Box P$).
Le système K
Le système $\textbf{K}$ est le plus petit système formel qui contient :
- chaque tautologie du calcul des propositions
- $\text{(K)}$ : $\Box(P\rightarrow Q)\rightarrow (\Box P\rightarrow \Box Q)$
- $\text{(dual)}$ : $\Diamond P\leftrightarrow\neg\Box\neg P$
Le système $\textbf{K}$ est minimal en ce sens qu’il est validé dans tout modèle.
Pour tout modèle $\mathcal{M}=\langle\mathcal{S},\mathcal{V}\rangle$ et tout nœud $a$, si $a\Vdash\Box(P\rightarrow Q)$ et $a\Vdash\Box P$, cela signifie que pour tout nœud $b$ tel que $a\longrightarrow b$, $b\Vdash P\rightarrow Q$ et $b\Vdash P$, par conséquent $b\Vdash Q$ et donc $a\Vdash \Box Q$.
Cela montre que l’axiome $\text{(K)}$ est valide dans tous les systèmes de transition.
Pour montrer que $P\rightarrow\Box P$ n’est pas prouvable dans $\textbf{K}$, il suffit donc de présenter un modèle (et le système $\textbf{K}$ autorise tous les systèmes de transition) où l’implication est fausse pour au moins un nœud. Or on a déjà vu un tel modèle :

Cet axiome $\text{(K)}$ (K en l’honneur de Kripke) est appelé axiome de distribution car il permet de distribuer l’opérateur modal $\Box$ à l’intérieur de l’implication. On l’appelle aussi parfois axiome d’omniscience logique car il stipule que si un agent sait que $P$ implique $Q$, alors s’il sait également que $P$ il doit savoir que $Q$. En d’autres termes, l’agent doit connaître toutes les conséquences logiques de ce qu’il sait déjà.
L’axiome $\text{(dual)}$ permet, lui, de passer d’un opérateur modal à l’autre et est aussi valide dans tout sytème de transition (être sûr de la présence d’un truc revient à ne pas être sûr de son absence, ou pour rester sur la structure du système de transition, dire qu’il existe un chemin vers $P$ revient à ne pas dire que tous les chemins vont vers $\neg P$).
La relation sœur permettant de passer de l’opérateur boite à l’opérateur diamant $\Box P \leftrightarrow \neg\Diamond\neg P$ (si tous les chemins mènent à $P$, il n’existe pas de chemin menant à $\neg P$) est elle aussi vraie partout.
Ces deux relations soulignent bien la nature duale des opérateurs $\Diamond$ et $\Box$.
Mais ce système formel n’est pas encore suffisamment riche pour contenir toutes les formules valides dans tous les modèles quels qu’ils soient. Pour cela, il faudrait également considérer toutes les substitutions uniformes possibles (entre autre dans la formule $\text{(K)}$). On passe alors aux logiques modales.
Logique modale normale
Une logique modale normale $\mathbb{L}$ est un ensemble de formules qui contient le système formel $\textbf{K}$ et qui est clos par :
- modus ponens $$ \begin{prooftree} \AxiomC{$\phi$} \AxiomC{$\phi\rightarrow\psi$} \RightLabel{$\scriptsize\;mod.p.$} \BinaryInfC{$\psi$} \end{prooftree} $$
- substitution uniforme $$ \begin{prooftree} \AxiomC{$\phi$} \RightLabel{$\scriptsize\;sub.$} \UnaryInfC{$\phi[\theta/P]$} \end{prooftree} $$
- nécessitation $$ \begin{prooftree} \AxiomC{$\phi$} \RightLabel{$\scriptsize\;nec.$} \UnaryInfC{$\Box\phi$} \end{prooftree} $$
Toute logique modale normale contient chaque formule $\phi$ prouvable dans le système formel $\textbf{K}$ (si $\vdash_\textbf{K}\phi$ alors $\phi$ fait partie de toute logique modale normale).
La plus petite logique modale normale est construite sur la base du système formel $\textbf{K}$. On la note $\mathbb{L}_\textbf{K}$. Le lien entre la logique normale $\mathbb{L}_\textbf{K}$ et le système formel $\textbf{K}$ est le suivant : $\phi \in \mathbb{L}_\textbf{K}$ ssi $\vdash_\textbf{K}\phi$.
Quelques axiomes usuels
$\text{(K) :}$ $\Box(P\rightarrow Q)\rightarrow(\Box P\rightarrow \Box Q)$
On l’a vu, l’axiome $\text{(K)}$ est à la base des logiques modales normales.
$\text{(D) :}$ $\Box P\rightarrow \Diamond P$
La formule $\text{(D)}$ dit que si quelque chose est nécessaire, alors elle doit être possible. On peut aussi l’interpréter différemment dans d’autres types de logiques que nous allons entrevoir ensuite : en logique déontique, la formule dit que quelque chose d’obligatoire doit être permis ; en logique épistémique, elle dit que si je sais $P$, alors il est faux que je sache $\neg P$ ; et en logique doxastique, que si je crois que $P$, alors il est faux que je crois que $\neg P$.
$\text{(D)}$ est parfois appelé axiome de consistance.
Comme on l’a vu plus tôt, un système de transition qui valide $\text{(D)}$ n’admet pas d’impasse. Autrement dit, les arcs doivent être non bornés à droite.
$\text{(T) :}$ $\Box P\rightarrow P$
La formule $\text{(T)}$ dit que si quelque chose est nécessaire, alors elle est. On l’appelle parfois axiome de factivité.
En logique déontique : ce qui est obligatoire est.
En logique épistémique : si je sais $P$, alors $P$ est avéré.
En logique doxastique : si je crois que $P$, alors $P$ est également avéré.
Et nous avons vu qu’un système de transition valide $\text{(T)}$ si et seulement si ce système est réflexif. $\text{(T)}$ est donc aussi l’axiome de réflexivité.
$\text{(B) :}$ $P\rightarrow \Box\Diamond P$
La formule $\text{(B)}$ dit que si quelque chose est vraie, alors il est nécessaire qu’elle soit possible.
En logique déontique : ce qui est, est obligatoirement permis.
En logique épistémique : si je $P$ est avéré, alors je sais que je ne sais pas $\neg P$.
En logique doxastique : si $P$ est avéré, alors je crois que je ne crois pas $\neg P$.
Et nous avons vu qu’un système de transition valide $\text{(B)}$ si et seulement si ce système est symétrique. $\text{(B)}$ est donc aussi l’axiome de symétrie.
$\text{(4) :}$ $\Box P\rightarrow \Box\Box P$
La formule $\text{(4)}$ dit que si quelque chose est nécessaire, alors elle est nécessairement nécessaire.
En logique déontique : si quelque chose est obligatoire, c’est obligatoire qu’elle le soit.
En logique épistémique : si je sais $P$, alors je sais que je sais $P$. Et transitivement, on sait que l’on sait que l’on sait… Autrement dit, avec la formule (4) nous décrivons des agents parfaitement rationnel.
On appelle $\text{(4)}$ l’axiome d’introspection positive dans le cadre de la logique épistémique.
Et nous avons vu qu’un système de transition valide $\text{(4)}$ si et seulement si ce système est transitif. $\text{(4)}$ est donc aussi l’axiome de transitivité.
$\text{(5) :}$ $\Diamond P\rightarrow \Box\Diamond P$
La formule $\text{(5)}$ dit que s’il n’est pas nécessaire que quelque chose ne soit pas, alors elle est nécessaire.
En logique déontique : si quelque chose est permise, c’est obligatoire qu’elle soit permise.
En logique épistémique : si je ne sais pas quelque chose, alors je sais que je ne le sais pas. L’interprétation épistémique décrit un agent parfaitement conscient de ce qu’il ne sait pas.
En logique doxastique : si je ne crois pas quelsue chose, alors je crois que je ne le crois pas. L’interprétation doxastique décrit un agent parfaitement conscient de ce qu’il ne croit pas.
On appelle $\text{(5)}$ l’axiome d’introspection négative dans le cadre de la logique épistémique.
Et nous avons vu qu’un système de transition valide $\text{(5)}$ si et seulement si ce système est euclidien. $\text{(5)}$ est donc aussi l’axiome d’euclidité.
En prenant ensemble les formules $\text{(5)}$ et $\text{(T)}$, on regarde des systèmes de transition à la fois euclidiens et réflexifs. Or la conjonction de ces deux propriétés est équivalentes à la conjonction des trois propriétés d’une relation d’équivalence !
Un système de transition est à la fois euclidien et réflexif si et seulement si il est à la fois réflexif, symétrique et transitif.
Autrement dit, un graphe euclidien et réflexif est en fait ni plus ni moins qu’un graphe dans lequel la relation d’accessibilité est une relation d’équivalence (relation définie par les trois propriétés réflexivité, symétrie et transitivité).
- $\Rightarrow$ :
- réflexif : c'est immédiat
- symétrique : si on a un arc $a\longrightarrow b$, alors par réflexivité, on a aussi $a\longrightarrow a$, et le caractère euclidien impose donc $b\longrightarrow a$.
- transitif : supposons qu'on ait deux arcs $a\longrightarrow b$ et $b\longrightarrow c$. Comme on a montré la symétrie du graphe, on a aussi un arc $b\longrightarrow a$ et le caractère euclidien impose donc un arc $a\longrightarrow c$.
- $\Leftarrow$ :
- réflexif : c'est immédiat
- euclidien : supposons qu'on ait deux arcs $a\longrightarrow b$ et $a\longrightarrow c$. La symétrie donne un arc $b\longrightarrow a$ et la transitivité impose alors un arc $b\longrightarrow c$.
Quelques systèmes formels et logiques usuels
Par la suite, nous confonderons un système formel et la logique qu’il induit par clôture. Les systèmes formels qu’on va introduire sont tous des extensions du système $\textbf{K}$.
- $\textbf{K}$
- $\textbf{KD}$ : $\textbf{K}\cup\set{\text{(D)}}$
- $\textbf{KB}$ : $\textbf{K}\cup\set{\text{(B)}}$
- $\textbf{KT}$ : $\textbf{K}\cup\set{\text{(T)}}$
- $\textbf{K4}$ : $\textbf{K}\cup\set{\text{(4)}}$
- $\textbf{KB4}$ : $\textbf{K}\cup\set{\text{(B),(4)}}$
- $\textbf{KD4}$ : $\textbf{K}\cup\set{\text{(D),(4)}}$
- $\textbf{KDB}$ : $\textbf{K}\cup\set{\text{(D),(B)}}$
- $\textbf{KTB}$ : $\textbf{K}\cup\set{\text{(T),(B)}}$
- $\textbf{S4} = \textbf{KT4}$ : $\textbf{K}\cup\set{\text{(T),(4)}}$
- $\textbf{S5} = \textbf{KT5}$ : $\textbf{K}\cup\set{\text{(T),(5)}}$
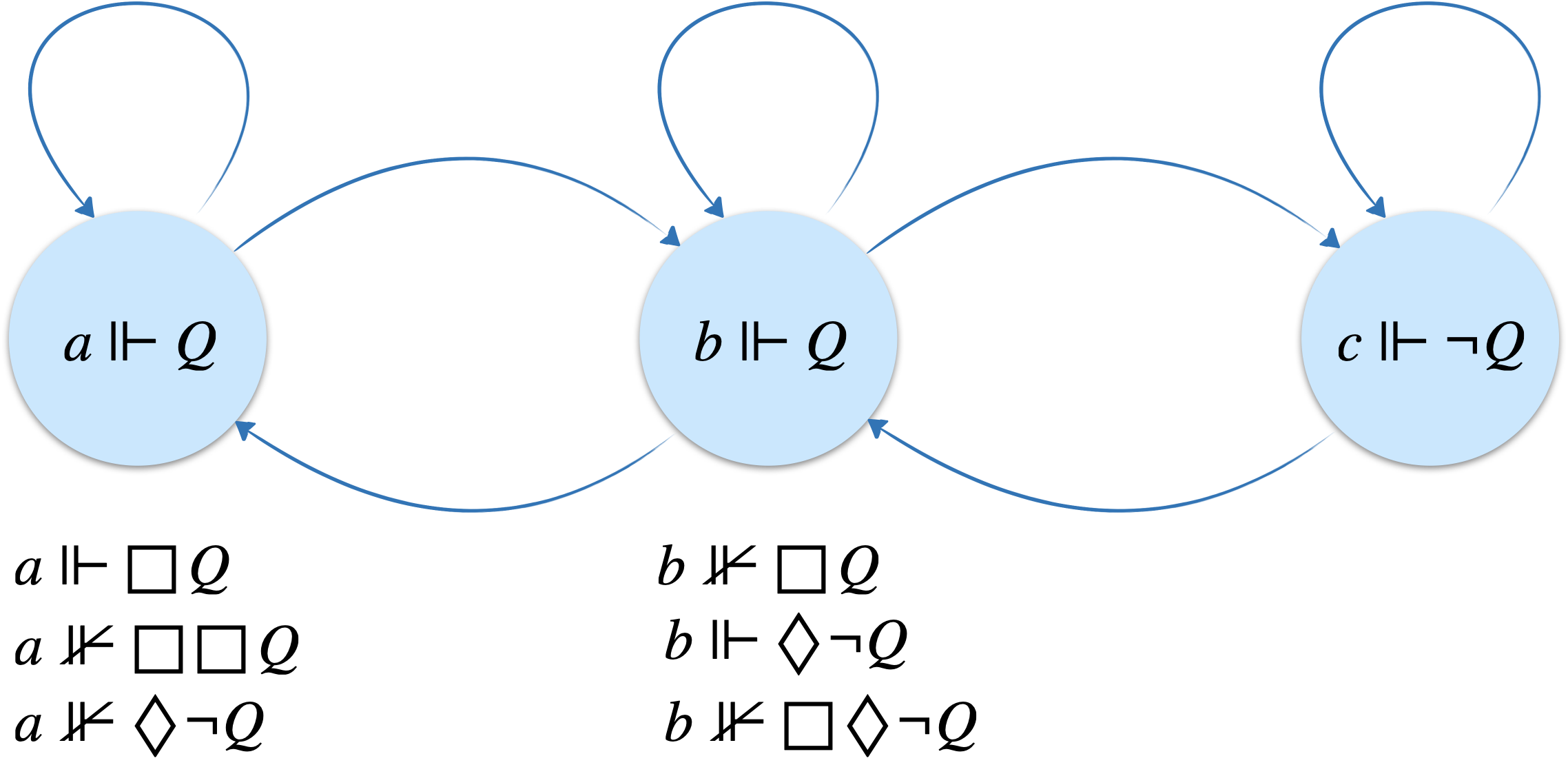
Convainquons-nous dans un premier temps que ces axiomes apportent bien quelque chose de plus en montrant par exemple que la logique $\textbf{KB}$ ne permet pas de prouver l’axiome $\text{(4)}$.
Comme $\text{(B)}$ est vraie dans tout système de transition symétrique, il suffit de trouver un modèle symétrique où au moins un nœud ne satisfait pas $\text{(4)}=\Box P\rightarrow\Box\Box P$ pour montrer que $\textbf{K4}\not\subseteq \textbf{KB}$.

De même, montrons que $\textbf{KTB}$ ne peut prouver ni $\text{(4)}$ ni $\text{(5)}$.
$\text{(T)}$ et $\text{(B)}$ seront vraies ensemble dans tout système de transition à la fois réflexif et symétrique. Exhibons un tel modèle où au moins un nœud ne satisfait ni $\text{(4)}=\Box P\rightarrow\Box\Box P$ ni $\text{(5)}=\Diamond P\rightarrow\Box\Diamond P$.
Mais on va préférer dans la suite mettre au jour les inclusions inverses (qui contient qui) grâce à la notion de réduction.
Soient $\textbf{S}$ et $\textbf{S’}$ deux systèmes formels et $\phi$ une formule quelconque,
$\textbf{S}≤\textbf{S'}$ si et seulement si $\vdash_\textbf{S}\phi\rightarrow \,\vdash_\textbf{S'}\phi$
Cette relation est réflexive ($\textbf{S}≤\textbf{S}$) et transitive (si $\textbf{S}≤\textbf{S’}$ et $\textbf{S’}≤\textbf{S’’}$ alors $\textbf{S}≤\textbf{S’’}$).
$\textbf{S}≤\textbf{S’}$ se lit $\textbf{S}$ se réduit à $\textbf{S’}$. Tout ce qui est prouvé à l’aide de $\textbf{S}$ peut également l’être à l’aide de $\textbf{S’}$.
Si $\textbf{S}$ se réduit à $\textbf{S’}$, cela signifie que $\textbf{S’}$ permet de prouver au moins autant de formules (appelées théorèmes) que $\textbf{S}$ et par conséquent, que la classe des systèmes de transition dans lesquels tous les théorèmes de $\textbf{S’}$ sont valides est incluse dans celle des systèmes de transition qui tous valident les théorèmes de $\textbf{S}$ (c’est plus dur de raconter plus de choses, ça restreint l’ensemble des modèles possibles).
Autrement dit,
si $\mathscr{C}_\textbf{S}$ et $\mathscr{C}_\textbf{S’}$ désignent respectivement la classe de tous les systèmes de transition qui valident $\textbf{S}$ et $\textbf{S’}$ :
$\textbf{S}≤\textbf{S'}$ si et seulement si $\mathscr{C}_\textbf{S'}\subseteq\mathscr{C}_\textbf{S}$.
Par contre, les logiques modales normales étant des ensembles de formules satisfaites, pour elles l’inclusion est dans l’autre sens :
Lorsque $\textbf{S}$ et $\textbf{S’}$ contiennent tous les deux le système formel $\textbf{K}$, les logiques modales normales qu’ils engendrent ($\mathbb{L}_\textbf{S}$ et $\mathbb{L}_\textbf{S’}$) vérifient la relation suivante :
$\textbf{S}≤\textbf{S'}$ si et seulement si $\mathbb{L}_\textbf{S}\subseteq\mathbb{L}_\textbf{S'}$.
On obtient alors immédiatement les réductions suivantes :
- $\textbf{K}≤\textbf{K4}$
- $\textbf{K}≤\textbf{KB}$
- $\textbf{K}≤\textbf{KD}$
- $\textbf{K4}≤\textbf{KB4}$
- $\textbf{K4}≤\textbf{KD4}$
- $\textbf{KB}≤\textbf{KB4}$
- $\textbf{KB}≤\textbf{KDB}$
- $\textbf{KD}≤\textbf{KDB}$
- $\textbf{KD}≤\textbf{KD4}$
- $\textbf{KT}≤\textbf{KTB}$
- $\textbf{KT}≤\textbf{KT4}$
Montrons maintenant que :
$\textbf{KD}≤\textbf{KT}$
Il suffit de montrer que la formule $\text{(D)}$ peut être prouvée grâce au système $\textbf{KT}$, c’est-à-dire : $\vdash_\textbf{KT} \Box P\rightarrow\Diamond P$.

On en déduit immédiatement :
- $\textbf{KDB}≤\textbf{KTB}$
- $\textbf{KD4}≤\textbf{ KT4=S4}$
On peut aussi montrer que :
$\textbf{KTB}≤\textbf{S5}$
Il suffit de montrer que la formule $\text{(B)}$ peut être prouvée grâce au système $\textbf{KT5}$, c’est-à-dire : $\vdash_\textbf{S5} P\rightarrow\Box\Diamond P$.
Montrons d’abord que $\vdash_\textbf{KT}P\rightarrow\Diamond P$, ce qui montre également que $\vdash_\textbf{KT5}P\rightarrow\Diamond P$.
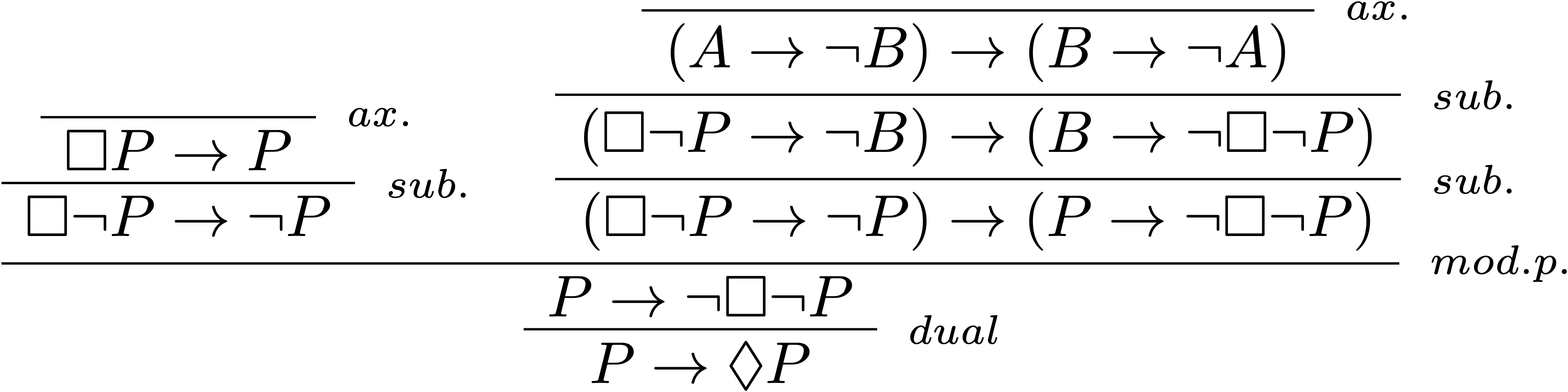
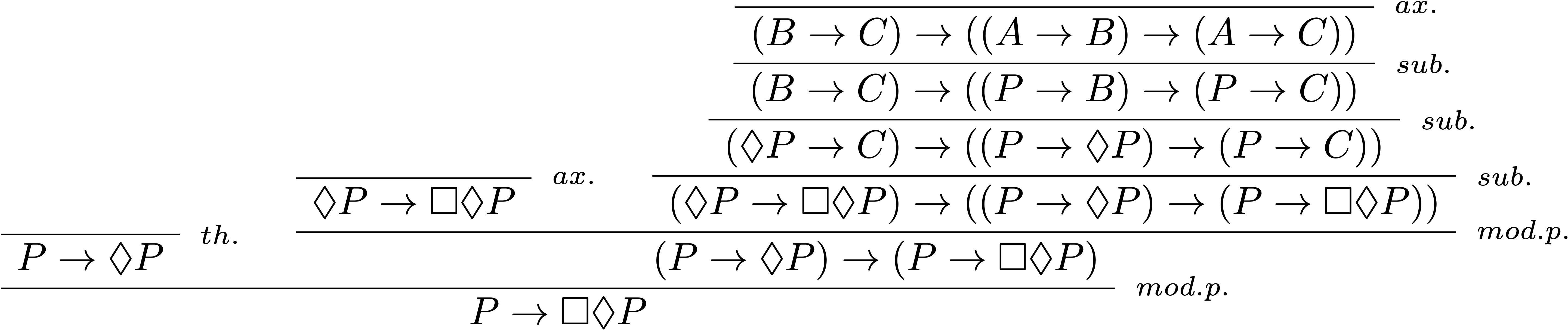
$\textbf{S4}≤\textbf{S5}$
Il suffit de montrer que la formule $\text{(4)}$ peut être prouvée grâce au système $\textbf{KT5}$, c’est-à-dire : $\vdash_\textbf{S5} \Box P\rightarrow\Box\Box P$.
On commence par montrer $\vdash_\textbf{S5} \Box P\rightarrow\Box\Diamond\Box P$ en ajoutant juste une substitution au théorème précédant :
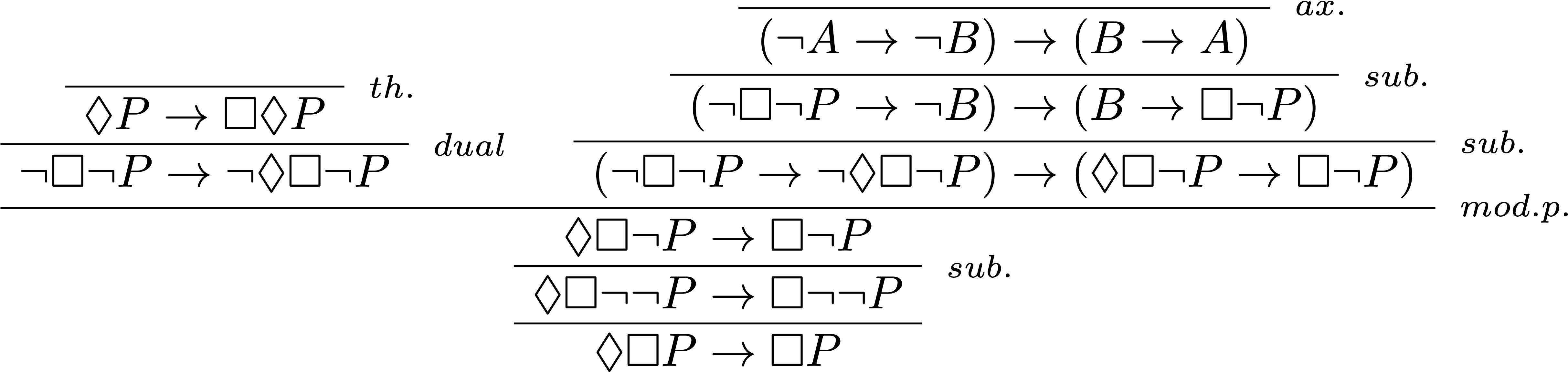
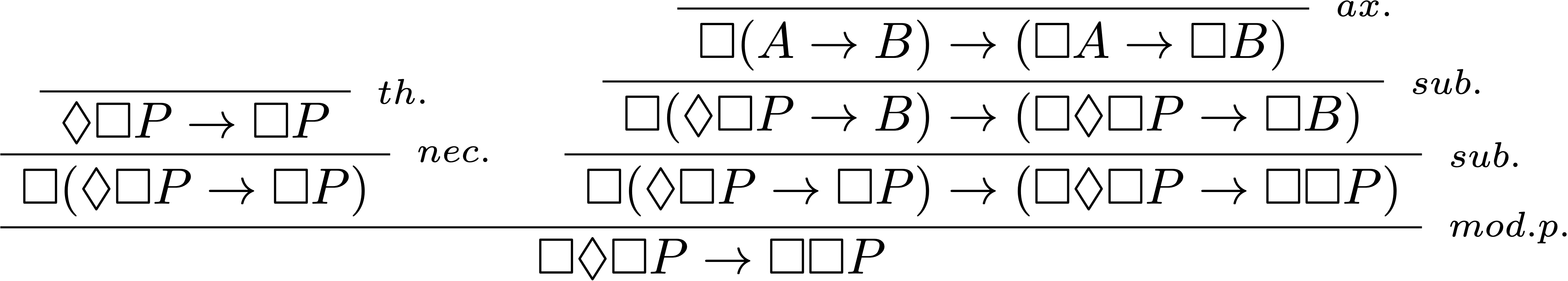
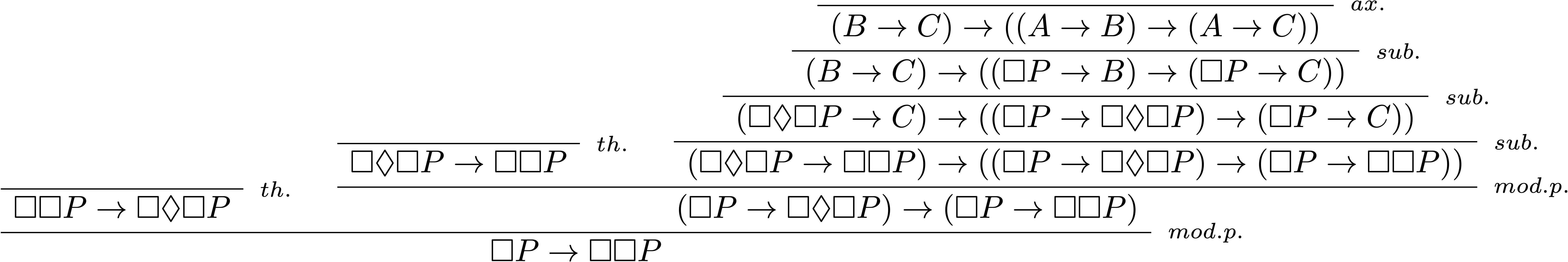
$\textbf{KB4}≤\textbf{S5}$
Il faut montrer à la fois que :
- la formule $\text{(4)}$ peut être prouvée dans le système $\textbf{S5}$ et on l'a fait dans la démonstration de la réduction de $\textbf{S4}$ à $\textbf{S5}$,
- la formule $\text{(B)}$ peut être prouvée dans le système $\textbf{S5}$ et on l'a fait dans la démonstration de la réduction de $\textbf{KTB}$ à $\textbf{S5}$,
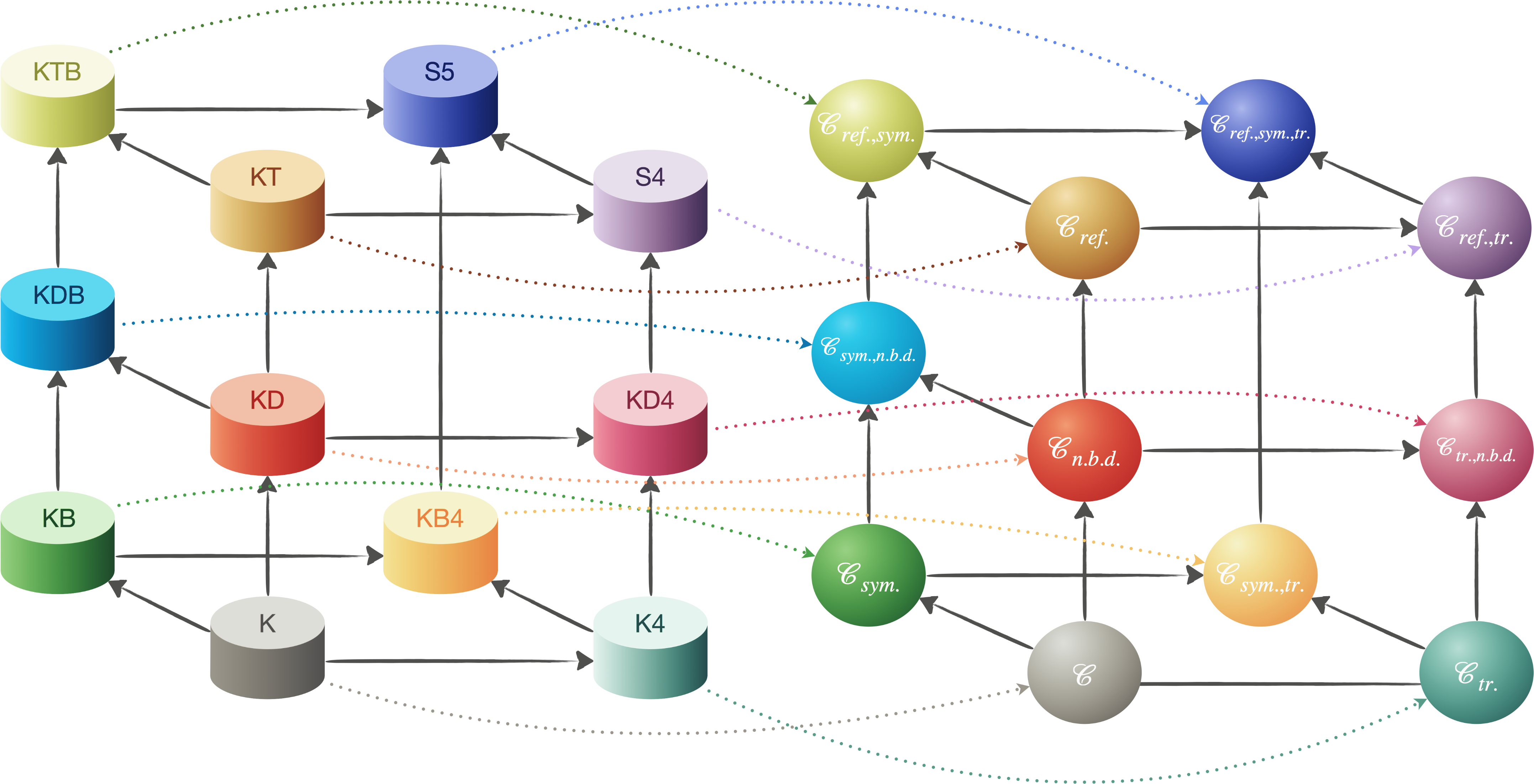
Représentons tout ça graphiquement en utilisant le code suivant : une flèche allant de $\textbf{S}$ à $\textbf{S’}$ signifie que la relation $\textbf{S}≤\textbf{S’}$ est avérée ($\textbf{S}$ se réduit à $\textbf{S’}$).
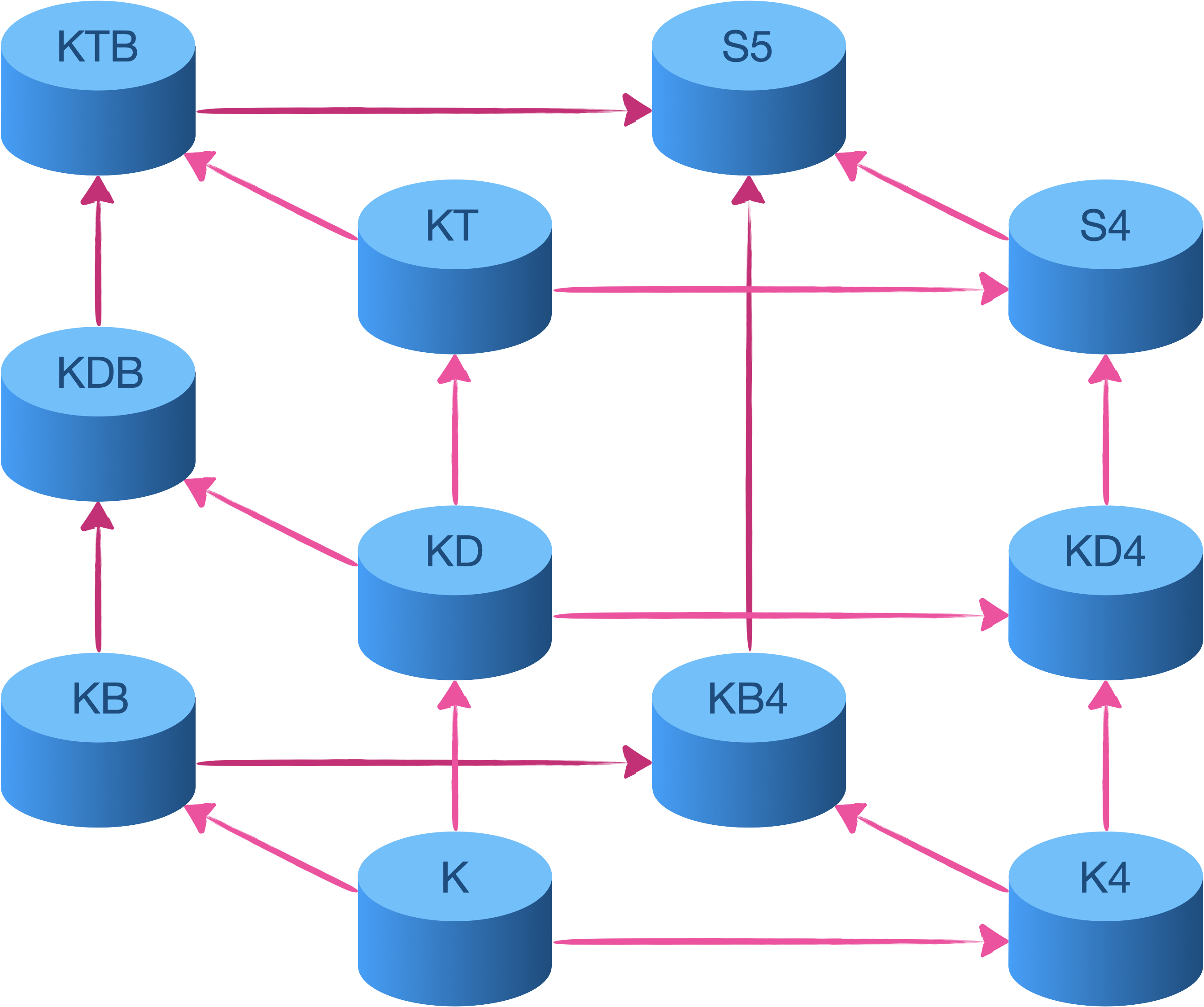
Et comme on l’a vu, la réduction d’un système formel à un autre implique l’inclusion inverse entre les classes de tous les systèmes de transition qui valident ces systèmes formels.
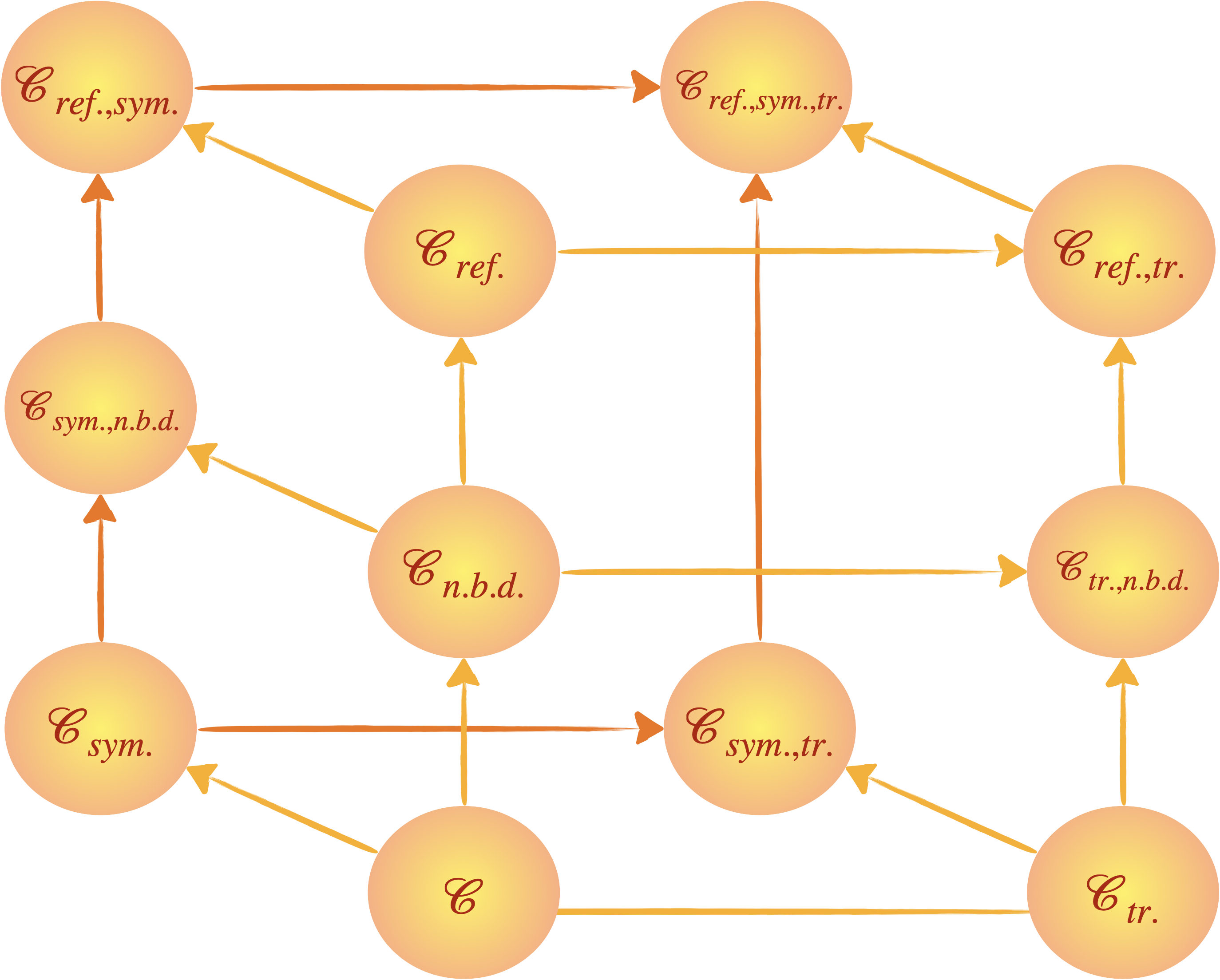
Dans le graphique suivant, une flèche allant de $\mathscr{C}$ à $\mathscr{C’}$ désigne donc l’inclusion inverse $\mathscr{C}\supseteq\mathscr{C’}$.
Le projet est maintenant de préciser le rapport entre axiomatique et sémantique avec l’espoir que l’ensemble des formules valides sur les structures d’un certain type soit identique à l’ensemble des axiomes et théorèmes d’un certain système (ce qu’on a appelé une logique modale), car ainsi la validité formera une interprétation du système. Mais pour s’assurer de cette adéquation entre sémantique et axiomatique, il faut d’une part obtenir la correction (ou solidité, soundness en anglais) du système (toutes les formules prouvables sont vraies), et sa réciproque, la complétude (toutes les formules vraies sont prouvables).
Dit autrement, on doit pouvoir déduire du système formel tout le vrai (complétude) et rien que le vrai (correction).
On va d’abord chercher à faire correspondre une logique modale normale à chaque classe de systèmes de transitions.
Soit $\mathscr{C}$ une classe de systèmes de transition et $\mathbb{L}$ une logique modale normale, $\mathbb{L}$ est correcte par rapport à la classe $\mathscr{C}$ (noté $\mathscr{C}$-correcte) si pour toute formule $\phi$ et pour tout système de transition $\mathcal{S}$ de la classe $\mathscr{C}$, si $\vdash_\mathbb{L}\phi$ alors $\mathcal{S}\Vdash^{\forall a,\forall \mathcal{V}}\phi$.
Ce qu’on peut aussi écrire :
$$\text{si } \vdash_\mathbb{L}\phi \text{ alors }\models_{\mathscr{C}}\phi$$
À chacune des onze classes, on peut faire correspondre une logique modale normale qui se trouve être correcte pour cette classe.
- si $\vdash_\textbf{K}\phi$ alors $\models_{\mathscr{C}}\phi$
- si $\vdash_\textbf{K4}\phi$ alors $\models_{\mathscr{C}_{tr.}}\phi$
- si $\vdash_\textbf{KD}\phi$ alors $\models_{\mathscr{C}_{n.b.d.}}\phi$
- si $\vdash_\textbf{KD4}\phi$ alors $\models_{\mathscr{C}_{tr.,n.b.d.}}\phi$
- si $\vdash_\textbf{KT}\phi$ alors $\models_{\mathscr{C}_{ref.}}\phi$
- si $\vdash_\textbf{S4}\phi$ alors $\models_{\mathscr{C}_{ref.,tr.}}\phi$
- si $\vdash_\textbf{KB}\phi$ alors $\models_{\mathscr{C}_{sym.}}\phi$
- si $\vdash_\textbf{KB4}\phi$ alors $\models_{\mathscr{C}_{sym.,tr.}}\phi$
- si $\vdash_\textbf{KDB}\phi$ alors $\models_{\mathscr{C}_{sym.,n.b.d.}}\phi$
- si $\vdash_\textbf{KTB}\phi$ alors $\models_{\mathscr{C}_{ref.,sym.}}\phi$
- si $\vdash_\textbf{S5}\phi$ alors $\models_{\mathscr{C}_{ref.,sym.,tr.}}\phi$
On a déjà en fait déjà tout démontré.
En effet, on a montré que les axiomes de la logique normale minimale (tautologies du calcul des propositions, $\text{(K)}$ et $\text{(dual)}$) sont satisfaites en tout nœud et pour toute valuation de tous les systèmes de transitions. Et on a montré que les trois opérations utilisés pour les preuves (la nécéssitation, la substitution uniforme et le modus ponens) préservent la validité. Donc une formule prouvable dans $\textbf{K}$ est valide dans tout système de transition ( $\textbf{K}$ est $\mathscr{C}$-correcte).
Ensuite, on a montré que chacun des axiomes modaux supplémentaires ajoutés à $\textbf{K}$ pour obtenir les autres logiques normales ont une validité limitée à une classe spécifique de systèmes de transition.
- $\text{(T)}$ est valide dans tout système de transition réflexif.
- $\text{(B)}$ est valide dans tout système de transition symétrique.
- $\text{(4)}$ est valide dans tout système de transition transitif.
- $\text{(D)}$ est valide dans tout système de transition non borné à droite.
- $\text{(4)}$ est valide dans tout système de transition euclidien.
Et on a montré qu’un graphe est à la fois réflexif et euclidien si et seulement si il est réflexif, symétrique et transitif.
On représente graphiquement par une flèche “$\textbf{X}\longrightarrow\mathscr{C}_x$” la relation de correction : “si $\vdash_\textbf{X}\phi$, alors $\models_{\mathscr{C}_x}\phi$”.
On va essayer maintenant d’associer les classe aux logiques, la sémantique à la syntaxe.
Soit $\mathscr{C}$ une classe de systèmes de transition et $\mathbb{L}$ une logique modale normale.
- $\mathbb{L}$ est faiblement complète par rapport à la classe $\mathscr{C}$ (noté $\mathscr{C}$-faiblement complète) si pour toute formule $\phi$ :
$$\text{si }\models_\mathscr{C}\phi \text{ alors } \vdash_\mathbb{L}\phi$$ - $\mathbb{L}$ est fortement complète par rapport à la classe $\mathscr{C}$ (noté $\mathscr{C}$-fortement complète) si pour toute formule $\phi$ et tout ensemble de formules $\Gamma$ :
$$\text{si } \Gamma \models_\mathscr{C}\phi \text{ alors } \Gamma \vdash_\mathbb{L}\phi$$
On a alors le théorème de forte complétude suivant :
- si $\Gamma\models_{\mathscr{C}}\phi$ alors $\Gamma\vdash_\textbf{K}\phi$
- si $\Gamma\models_{\mathscr{C}_{tr.}}\phi$ alors $\Gamma\vdash_\textbf{K4}\phi$
- si $\Gamma\models_{\mathscr{C}_{n.b.d.}}\phi$ alors $\Gamma\vdash_\textbf{KD}\phi$
- si $\Gamma\models_{\mathscr{C}_{tr.,n.b.d.}}\phi$ alors $\Gamma\vdash_\textbf{KD4}\phi$
- si $\Gamma\models_{\mathscr{C}_{ref.}}\phi$ alors $\Gamma\vdash_\textbf{KT}\phi$
- si $\Gamma\models_{\mathscr{C}_{ref.,tr.}}\phi$ alors $\Gamma\vdash_\textbf{S4}\phi$
- si $\Gamma\models_{\mathscr{C}_{sym.}}\phi$ alors $\Gamma\vdash_\textbf{KB}\phi$
- si $\Gamma\models_{\mathscr{C}_{sym.,tr.}}\phi$ alors $\Gamma\vdash_\textbf{KB4}\phi$
- si $\Gamma\models_{\mathscr{C}_{sym.,n.b.d.}}\phi$ alors $\Gamma\vdash_\textbf{KDB}\phi$
- si $\Gamma\models_{\mathscr{C}_{ref.,sym.}}\phi$ alors $\Gamma\vdash_\textbf{KTB}\phi$
- si $\Gamma\models_{\mathscr{C}_{ref.,sym.,tr.}}\phi$ alors $\Gamma\vdash_\textbf{S5}\phi$
Pour le démontrer on va avoir besoin de nouvelles définitions et de plusieurs lemmes.
Soient $\textbf{S}$ un système formel et $\Gamma$ un ensemble de formules,
$\Gamma$ est $\textbf{S}$-consistant si et seulement si $\Gamma\nvdash_\textbf{S}\bot$.
Dans le cas contraire, $\Gamma$ est dit $\textbf{S}$-inconsistant.Soient $\mathscr{C}$ une classe de système de transition et $\mathbb{L}$ une logique modale normale,
$\mathbb{L}$ est $\mathscr{C}$-(fortement) complète si et seulement si pour tout $\Gamma\subseteq\mathbb{L}$ qui est $\mathbb{L}$-consistant, il existe $\mathcal{S}\in\mathscr{C},\mathcal{V}$ et $a$ tels que $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\Gamma$.
- $\Rightarrow$ :
puisque $\mathbb{L}$ est $\mathscr{C}$-complète, un ensemble de formules quelconque $\mathbb{L}$-consistant $\Gamma\subseteq\mathbb{L}$ est nécessairement satisfaisable pour un système de transition de la classe $\mathscr{C}$. En effet, si ce n'était pas le cas, l'expression $\Gamma\models_\mathscr{C}\bot$ serait vraie, mais alors nous pourrions en déduire $\Gamma\vdash_\mathbb{L}\bot$ en utilisant la $\mathscr{C}$-complétude de $\mathbb{L}$. - $\Leftarrow$ :
montrons la contraposée. On suppose donc que $\mathbb{L}$ n'est pas $\mathscr{C}$-complète. Soit donc $\Gamma$ un ensemble de formules et $\phi$ une formule tels que $\Gamma\models_\mathscr{C}\phi$ mais $\Gamma\nvdash_\mathbb{L}\phi$. Il apparaît dès lors que $\Gamma\cup\set{\neg\phi}\nvdash_\mathbb{L}\bot$ est vérifiée, car $\Gamma\cup\set{\neg\phi}\vdash_\mathbb{L}\bot$ entraînerait $\Gamma\vdash_\mathbb{L}\neg\phi\rightarrow\bot$ puis, en passant par la contraposée, $\Gamma\vdash_\mathbb{L}\phi$. Par conséquent $\Gamma\cup\set{\neg\phi}$ est $\mathbb{L}$-consistant et pourtant, pour tout système de transition $\mathcal{S}\in\mathscr{C}$, $\mathcal{V}$ et $a$, $\langle\mathcal{S},\mathcal{V},a\rangle\nVdash\Gamma\cup\set{\neg\phi}$.
L’idée pour démontrer la complétude est de chercher un modèle $\langle\mathcal{S},\mathcal{V}\rangle$ dont le système de transition fait partie de la classe considérée et un nœud $a$ tels que $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\Gamma$ où $\Gamma$ est un ensemble de formules $\mathbb{L}$-consistant.
On va mettre au point un tel modèle en modelant les nœuds de son système de distribution directement à partir d’ensembles de formules ! La sémantique détourne ainsi la syntaxe à son profit en donnant vie à une sorte de Golem syntaxique.
Soient $\mathbb{L}$ une logique modale normale et $\Gamma$ un ensemble de formules,
$\Gamma$ est maximal $\mathbb{L}$-consistant (MC) si et seulement si $\Gamma\nvdash_\mathbb{L}\bot$ et pour tout ensemble $\Gamma \subsetneq \Gamma'$, $\Gamma'\vdash_\mathbb{L}\bot$.
Remarques :
si $\Gamma$ est maximal $\mathbb{L}$-consistant, alors :
- $\mathbb{L}\subseteq\Gamma$
- $\Gamma$ est clos par modus ponens
- pour toute formule $\phi$, $\phi\in\Gamma$ ou $\neg\phi\in\Gamma$
- pour toutes formules $\phi$ et $\psi$, $\phi\lor\psi\in\Gamma$ si et seulement si $\phi\in\Gamma$ ou $\psi\in\Gamma$
Si $\Gamma$ est $\mathbb{L}$-consistant, alors il existe $\Gamma_{max}$ maximal $\mathbb{L}$-consistant tel que $\Gamma\subseteq\Gamma_{max}$.
Soit $(\phi_n)_{n\in\mathbb{N}}$ une énumération de toutes les formules. On définit :
- $\Gamma_0=\Gamma$
- $\Gamma_{n+1}=\begin{cases}\Gamma_n\cup\set{\phi_n} \text{ si } \Gamma_n\cup\set{\phi_n}\nvdash_\mathbb{L}\bot\\ \Gamma_n\cup\set{\neg\phi_n} \text{ sinon}\end{cases}$
- $\displaystyle \Gamma_{max}=\bigcup_{n\in\mathbb{N}}\Gamma_n$
$\Gamma_{max}$ est maximal car sinon il existerait $\Gamma’$ $\mathbb{L}$-consistant tel que $\Gamma_{max}\subsetneq\Gamma’$. Dans ce cas, une formule quelconque $\psi$ telle que $\psi\in\Gamma’\setminus\Gamma_{max}$ apparaîtrait dans l’énumération $(\phi_n)_{n\in\mathbb{N}}$ de toutes les formules et il existerait ainsi un entier $n$ tel que $\psi=\phi_n$. Par construction de $\Gamma_{max}$, comme $\phi_n\not\in\Gamma_{max}$, $\Gamma_n\cup\set{\phi_n}\vdash_\mathbb{L}\bot$ est vérifiée. Donc $\Gamma_{max}\cup\set{\phi_n}\vdash_\mathbb{L}\bot$ ce qui entraîne $\Gamma’\vdash_\mathbb{L}\bot$, contredisant la $\mathbb{L}$-consistance de $\Gamma’$.
Soit $\mathbb{L}$ une logique modale normale, le modèle canonique $\mathcal{M}_\mathbb{L}$ est défini par $\mathcal{M}_\mathbb{L}=\langle N_\mathbb{L},A_\mathbb{L},\mathcal{V}_\mathbb{L}\rangle$ avec :
- $N_\mathbb{L}=\set{\Gamma|\Gamma\text{ maximal }\mathbb{L}\text{-consistant}}$
- $A_\mathbb{L}$ défini par $\Gamma\longrightarrow\Gamma'$ si et seulement si pour toute formule $\phi$, si $\phi\in\Gamma'$ alors $\Diamond\phi\in\Gamma$ (c.-à-d. $\Gamma\supseteq\set{\Diamond\phi : \phi\in\Gamma'}$)
- $\mathcal{V}_\mathbb{L}$ est défini par $\mathcal{V}_\mathbb{L}(P)=\set{\Gamma\in N_\mathbb{L}|P\in\Gamma}$ (c.-à-d. $\Gamma\Vdash P$ si et seulement si $P\in\Gamma$)
Soit $\mathbb{L}$ une logique modale normale et $\mathcal{M}_\mathbb{L}=\langle N_\mathbb{L},A_\mathbb{L},\mathcal{V}_\mathbb{L}\rangle$ le modèle canonique associé à $\mathbb{L}$. Pour tout nœud $\Gamma,\Gamma’\in N_\mathbb{L}$, on a :
$\Gamma\longrightarrow\Gamma'$ si et seulement si pour toute formule $\phi$, si $\Box\phi\in\Gamma$ alors $\phi\in\Gamma'$.
- $\Rightarrow$ :
Raisonnons par l'absurde en supposant $\Box\phi\in\Gamma$ et $\phi\not\in\Gamma'$. Par maximale $\mathbb{L}$-consistance de $\Gamma'$, $\neg\phi\in\Gamma'$. Par définition de l'arc $\Gamma\longrightarrow\Gamma'$, $\Diamond\neg\phi\in\Gamma$ et puisque $\Gamma$ est consistant, $\neg\Diamond\neg\phi\not\in\Gamma$, d'où $\Box\phi\not\in\Gamma$ (où on a utilisé la dualité entre $\Diamond$ et $\Box$). Contradiction. - $\Leftarrow$ :
Soit $\phi\in\Gamma'$. Raisonnons par l'absurde en supposant $\Diamond\phi\not\in\Gamma$ (ce qui signifie que $\Gamma\,\,\not\!\!\longrightarrow\Gamma'$). Alors par maximale $\mathbb{L}$-consistance $\neg\Diamond\phi\in\Gamma$, par conséquent $\neg\Diamond\neg\neg\phi\in\Gamma$ et donc $\Box\neg\phi\in\Gamma$ (où on a utilisé la dualité entre $\Diamond$ et $\Box$). Par hypothèse, $\Box\neg\phi\in\Gamma$ entraîne $\neg\phi\in\Gamma'$, ce qui contredit la $\mathbb{L}$-consistance de $\Gamma'$.
Soit $\mathbb{L}$ une logique modale normale et $\mathcal{M}_\mathbb{L}=\langle N_\mathbb{L},A_\mathbb{L},\mathcal{V}_\mathbb{L}\rangle$ le modèle canonique associé à $\mathbb{L}$. Pour tout nœud $\Gamma,\Gamma’\in N_\mathbb{L}$ :
Si $\Diamond\phi\in\Gamma$ alors il existe $\Gamma'$ tel que $\Gamma\longrightarrow\Gamma'$ et $\phi\in\Gamma'$.
Supposons $\Diamond\phi\in\Gamma$. Pour obtenir $\Gamma’$, on construit d’abord $\Theta=\set{\phi}\cup\set{\psi|\Box\psi\in\Gamma}$. Cet ensemble est consistant car sinon il existerait $\psi_1,\ldots,\psi_k\in\Theta$ tels que $\vdash_\mathbb{L}(\psi_1\land\ldots\land\psi_k)\rightarrow\neg\phi$. Par nécessitation, $\vdash_\mathbb{L}\Box((\psi_1\land\ldots\land\psi_k)\rightarrow\neg\phi)$. Et par distributivité (utilisation de l’axiome $\text{(K)}$) $\vdash_\mathbb{L}\Box(\psi_1\land\ldots\land\psi_k)\rightarrow\Box\neg\phi$. Et puisque dans toute logique normale $\vdash_\mathbb{L}(\Box\psi_1\land\ldots\land\Box\psi_k)\rightarrow\Box(\psi_1\land\ldots\land\psi_k)$, on obtient finalement $\vdash_\mathbb{L}(\Box\psi_1\land\ldots\land\Box\psi_k)\rightarrow\Box\neg\phi$. Par conséquent $\Gamma\vdash_\mathbb{L}\Box\neg\phi$, ce qui implique que $\Box\neg\phi\in\Gamma$ par maximalité, et donc également $\neg\Diamond\phi\in\Gamma$ (par dualité). Or par hypothèse, $\Diamond\phi\in\Gamma$, ce qui entraîne l’inconsistance de $\Gamma$. Contradiction.
Comme on vient de montrer que l’ensemble $\Theta=\set{\phi}\cup\set{\psi|\Box\psi\in\Gamma}$ est $\mathbb{L}$-consistant, il suffit de prendre pour $\Gamma’$ l’ensemble $\Theta_{max}$ maximal $\mathbb{L}$-consistant donné par le lemme de Lindenbaum tel que $\Theta\subseteq\Theta_{max}$. On a bien ainsi un nœud de $N_\mathbb{L}$ contenant $\phi$.
Soit $\mathbb{L}$ une logique modale normale et $\mathcal{M}_\mathbb{L}=\langle N_\mathbb{L},A_\mathbb{L},\mathcal{V}_\mathbb{L}\rangle$ le modèle canonique associé à $\mathbb{L}$. Pour tout nœud $\Gamma\in N_\mathbb{L}$ :
$\langle\mathcal{M}_\mathbb{L},\Gamma\rangle\Vdash\phi$ si et seulement si $\phi\in\Gamma$
La démonstration se fait par induction sur la hauteur de la formule $\phi$.
- si $ht(\phi)=0$, alors $\phi=\top$ ou $\phi=\bot$ ou $\phi$ est une variable propositionnelle et $\Gamma\Vdash\phi$ ssi $\phi\in\Gamma$ est la définition même de la valuation $\mathcal{V}_\mathbb{L}$.
- si $ht(\phi)=n+1$
- si $\phi=\neg\psi$, alors $\Gamma\Vdash\neg\phi$ ssi $\Gamma\nVdash\psi$. Or par hypothèse d'induction $\Gamma\nVdash\psi$ ssi $\psi\not\in\Gamma$. Par maximalité de $\Gamma$, on obtient $\neg\psi\in\Gamma$.
- si $\phi=(\psi_1\lor\psi_2)$, alors $\Gamma\Vdash(\psi_1\lor\psi_2)$ ssi $\Gamma\Vdash\psi_1$ ou $\Gamma\Vdash\psi_2$.
Par hypothèse d'induction, $\Gamma\Vdash\psi_1$ ssi $\psi_1\in\Gamma$ et $\Gamma\Vdash\psi_2$ ssi $\psi_2\in\Gamma$. Et par maximalité de $\Gamma$, $\psi_1\in\Gamma$ ou $\psi_2\in\Gamma$ ssi $(\psi_1\lor\psi_2)\in\Gamma$. - si $\phi=(\psi_1\land\psi_2)$, alors $\Gamma\Vdash(\psi_1\lor\psi_2)$ ssi $\Gamma\Vdash\psi_1$ et $\Gamma\Vdash\psi_2$.
Par hypothèse d'induction, $\Gamma\Vdash\psi_1$ ssi $\psi_1\in\Gamma$ et $\Gamma\Vdash\psi_2$ ssi $\psi_2\in\Gamma$. Or par $\mathbb{L}$-consistance, $\psi_1\in\Gamma$ et $\psi_2\in\Gamma$ ssi $(\psi_1\land\psi_2)\in\Gamma$. - si $\phi=(\psi_1\rightarrow\psi_2)$. On déduit ce cas de $\neg\psi_1\lor\psi_2$.
- si $\phi=(\psi_1\leftrightarrow\psi_2)$. On déduit ce cas de $(\psi_1\rightarrow\psi_2)\land(\psi_2\rightarrow\psi_1)$.
- si $\phi=\Diamond\psi$, alors $\Gamma\Vdash\Diamond \psi$ ssi il existe $\Gamma',\Gamma\longrightarrow\Gamma'$ et $\Gamma'\Vdash\psi$. Or par hypothèse d'induction $\Gamma'\Vdash\psi$ ssi $\psi\in\Gamma'$. Finalement, par définition de la relation $\Gamma\longrightarrow\Gamma'$ et par le lemme ($\longrightarrow$ et $\Diamond$) $\psi\in\Gamma'$ ssi $\Diamond\psi\in\Gamma$.
- si $\phi=\Box\psi$, alors $\Gamma\Vdash\Box\phi$ ssi $\Gamma\Vdash\neg\Diamond\neg\psi$ ssi $\neg\Diamond\neg\psi\in\Gamma$ ssi $\Box\psi\in\Gamma$ (par maximal $\mathbb{L}$-consistance).
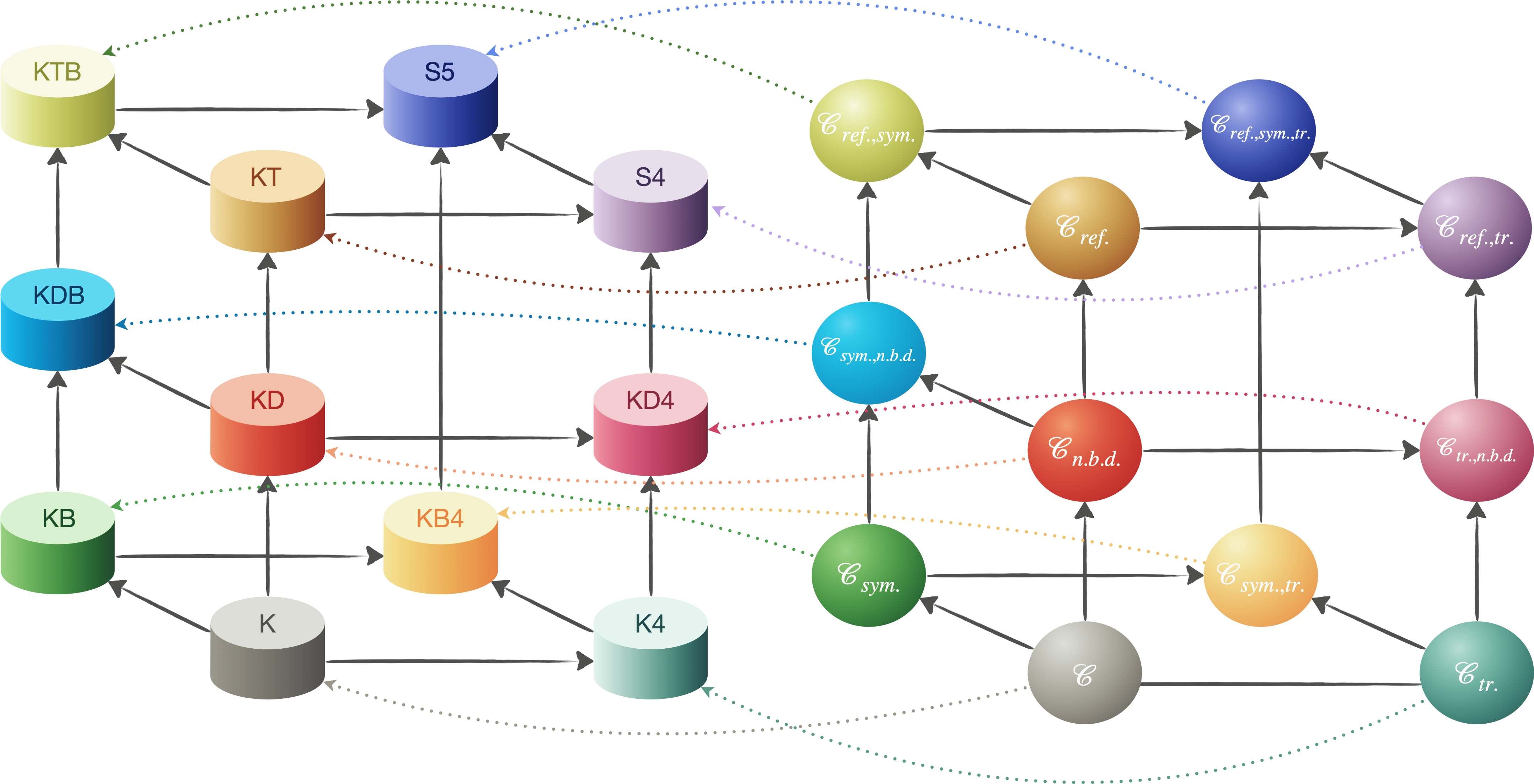
Nous voilà parés pour démontrer la complétude forte des onze logiques normales décrites grâce au modèle canonique de chacune.
Le lemme d’existence nous dit que $\mathbb{L}$ est $\mathscr{C}$-fortement complète ssi pour tout $\Gamma\subseteq\mathbb{L}$, $\mathbb{L}$-consistant, il existe $\mathcal{S}\in\mathscr{C}$, $\mathcal{V}$ et $a$ tels que $\langle\mathcal{S},\mathcal{V},a\rangle\Vdash\Gamma$.
Pour chaque logique normale, nous allons choisir le modèle canonique $\mathcal{M}_\mathbb{L}=\langle N_\mathbb{L},A_\mathbb{L},\mathcal{V}_\mathbb{L}\rangle$ associé. Et pour le nœud $a$, nous allons prendre $\Gamma_{max}$. Le lemme de vérité nous dit alors que $\langle\mathcal{M}_\mathbb{L},\Gamma_{max}\rangle\Vdash\phi$ ssi $\phi\in\Gamma_{max}$. En conséquence, puisque $\Gamma\subseteq\Gamma_{max}$, il ressort que $\langle\mathcal{M}_\mathbb{L},\Gamma_{max}\rangle\Vdash\Gamma$.
Il ne reste plus qu’à vérifier à chaque fois que le modèle canonique est bien construit sur la base d’un système de transition de la classe $\mathscr{C}$ considérée.
- $\mathcal{M}_\textbf{K}\in\mathscr{C}$ : comme $\mathscr{C}$ désigne la classe de tous les systèmes de transition, il n'ya rien à montrer.
- $\mathcal{M}_\textbf{K4}\in\mathscr{C}_{tr.}$ :
il faut montrer que pour tout nœud $\Xi_1$, $\Xi_2$ et $\Xi_3$ de $\mathcal{M}_\textbf{K4}$, si $\Xi_1\longrightarrow \Xi_2$ et $\Xi_2\longrightarrow \Xi_3$, alors $\Xi_1\longrightarrow \Xi_3$.
La formule $\text{(4)}=\Box p\rightarrow\Box\Box P$ est équivalente (par dualité) à la formule $\neg\Diamond\neg P\rightarrow\neg\Diamond\neg\neg\Diamond\neg P$ elle même équivalente à $\Diamond\Diamond\neg P\rightarrow\Diamond\neg P$ (en passant par la contraposée et en éliminant les doubles négations). Comme $\Diamond\Diamond\neg P\rightarrow\Diamond\neg P\in\Gamma$, on a aussi $\Diamond\Diamond\neg P\rightarrow\Diamond\neg P\in\Xi_1$ et puisque $\Xi_1$ est clos par substitution uniforme, $\Diamond\Diamond\neg \neg\phi\rightarrow\Diamond\neg \neg\phi\in\Xi_1$. Et donc chaque formule $\Diamond\Diamond\rightarrow\Diamond$ appartient à $\Xi_1$.
Par définition de $\Xi_1\longrightarrow \Xi_2$ et $\Xi_2\longrightarrow \Xi_3$, pour une formule $\phi$ quelconque, si $\phi\in\Xi_3$, alors $\Diamond\phi\in\Xi_2$ et $\Diamond\Diamond\phi\in\Xi_1$. Et comme $\Xi_1$ est clos par modus ponens, si à la fois $\Diamond\Diamond\phi\in\Xi_1$ et $\Diamond\Diamond\phi\rightarrow\Diamond\phi\in\Xi_1$, alors $\Diamond\phi\in\Xi_1$. Cela prouve que pour toute formule $\phi$, si $\phi\in\Xi_3$, alors $\Diamond\phi\in\Xi_1$, et par conséquent $\Xi_1\longrightarrow\Xi_3$. - $\mathcal{M}_\textbf{KD}\in\mathscr{C}_{n.b.d.}$ :
il faut montrer que pour tout nœud $\Xi_1$ de $\mathcal{M}_\textbf{KD}$, il existe $\Xi_2$ tel que $\Xi_1\longrightarrow \Xi_2$.
D'après le lemme ($\longrightarrow$ et $\Diamond$), si $\Diamond\phi\in\Xi_1$, alors il existe $\Xi_2$ tel que $\Xi_1\longrightarrow \Xi_2$ et $\phi\in\Xi_2$. Or l'axiome $\text{(D)}$ dit précisément $\Box P\rightarrow\Diamond P$. Comme $\Xi_1$ est clos par substitution uniforme, la formule $\Box\top\rightarrow\Diamond\top$ est dans $\Xi_1$. Or $\Xi_1$ vérifie nécessairement $\Box\top$ (car une tautologie est vraie partout) et comme $\Xi_1$ est clos par modus ponens, $\Diamond\top\in\Xi_1$, et donc d'après le lemme ($\longrightarrow$ et $\Diamond$), il existe $\Xi_2$ tel que $\Xi_1\longrightarrow \Xi_2$ et $\top\in\Xi_2$. - $\mathcal{M}_\textbf{KD4}\in\mathscr{C}_{tr.,n.b.d.}$ :
Conséquence de 2. et 3. - $\mathcal{M}_\textbf{KT}\in\mathscr{C}_{ref.}$ :
Il faut montrer que $\Xi\longrightarrow \Xi$ est vérifié pour tout nœud $\Xi$ de $\mathcal{M}_\textbf{KT}$.
La formule $\text{(T)}=\Box P\rightarrow P$ est équivalente à $\neg\Diamond\neg P\rightarrow P$ et par contraposition à $\neg P\rightarrow\diamond\neg P$. Comme $\Xi$ est clos par substitution uniforme, la formule $\neg \neg \phi\rightarrow\diamond\neg \neg\phi$ est dans $\Xi$ et donc $\phi\rightarrow\Diamond\phi$ est dans $\Xi$. La cloture par modus ponens permet alors de déduire que pour toute formule $\phi\in\Xi$, $\Diamond\phi\in\Xi$, ce qui est la condition nécessaire à la relation $\Xi\longrightarrow \Xi$. - $\mathcal{M}_\textbf{S4}\in\mathscr{C}_{ref.,tr.}$ :
Conséquence de 2. et 5. - $\mathcal{M}_\textbf{KB}\in\mathscr{C}_{sym.}$ :
il faut montrer que pour tout couple de nœuds $\Xi_1$ et $\Xi_2$ de $\mathcal{M}_\textbf{KB}$, $\Xi_1\longrightarrow \Xi_2$ alors $\Xi_2\longrightarrow \Xi_1$.
$\text{(B)}= P\rightarrow \Box\Diamond P$ . Comme $\Xi_1$ est clos par substitution uniforme, les formules $\phi\rightarrow\Box\Diamond\phi$ sont dans $\Xi_1$. La cloture par modus ponens de $\Xi_1$ nous dit alors que si $\phi\in\Xi_1$, alors $\Box\Diamond\phi\in\Xi_1$. Or d'après le lemme ($\longrightarrow$ et $\Box$), si $\Xi_1\longrightarrow\Xi_2$ alors pour toute formule $\phi$, si $\Box\phi\in\Xi_1$, alors $\phi\in\Xi_2$. Par conséquent, pour tout $\phi\in\Xi_1$, $\Diamond\phi\in\Xi_2$, ce qui est la condition nécessaire pour définir $\Xi_2\longrightarrow\Xi_1$. - $\mathcal{M}_\textbf{KB4}\in\mathscr{C}_{sym.tr.}$ :
Conséquence de 2. et 7. - $\mathcal{M}_\textbf{KDB}\in\mathscr{C}_{sym.,n.b.d.}$ :
Conséquence de 3. et 7. - $\mathcal{M}_\textbf{KTB}\in\mathscr{C}_{ref.sym.}$ :
Conséquence de 5. et 7. - $\mathcal{M}_\textbf{S5}\in\mathscr{C}_{ref.,sym.tr.}$ :
Conséquence de 2. et 5. et 7.
On représente graphiquement par une flèche “$\mathscr{C}_x\longrightarrow\textbf{X}$” la relation de forte-complétude : “si $\Gamma\models_{\mathscr{C}_x}\phi$, alors $\Gamma\vdash_\textbf{X}\phi$”.
La notion de conséquence sémantique $\models$ demande une satisfaction sur tous les modèle alors que la notion de conséquence syntaxique $\vdash$ demande seulement l’existence d’une preuve.
Dit autrement, $\models$ est définie avec un quantificateur universel $\forall$ et $\vdash$ avec un quantificateur existentiel $\exists$ or la négation du quantificateur universel est le quantificateur existentiel et inversement.
Démontrer qu’une formule est non démontrable est donc très difficile du côté de la théorie de la démonstration puisque cela oblige à montrer que toutes les preuves échouent. Par contre, sur le versant sémantique, il suffit de trouver un modèle où la négation de la formule est satisfaite (un contre-exemple suffit).
C’est la correction qui nous permet le changement de versant (on passe de la syntaxe à la sémantique).
On peut trouver d’ailleurs un peu douloureux que la correspondance de loin la plus difficile à démontrer (la complétude) apporte si peu d’applications concrètes.