
Notes de lecture du livre La logique pas à pas de Jacques Duparc que je paraphrase allégrement.
Calcul des propositions
Théorie de la démonstration
Une preuve ou une démonstration :
- est de longueur finie,
- est vérifiable mécaniquement,
- s’appuie sur des hypothèses,
- aboutit à une conclusion.
Une démonstration permet de mettre au jour une vérité syntaxique (s’appuyant sur un jeu de règles) plutôt que sémantique (faisant intervenir les modèles d’une théorie).
On a vu que $\phi$ est une conséquence sémantique de la théorie $\mathcal{T}$, noté $\mathcal{T}\models \phi$, si $\phi$ est vraie dans tous les modèles de $\mathcal{T}$.
On va maintenant se pencher sur la conséquence syntaxique de la théorie $\mathcal{T}$. $\phi$ est une conséquence syntaxique de $\mathcal{T}$, noté $\mathcal{T} \vdash \phi$, s’il existe une démonstration de $\phi$ sur la base d’hypothèses contenues dans la théorie $\mathcal{T}$. Fini les modèles, on ne s’intéresse plus qu’à la syntaxe par un jeu de réécriture.
Quel est le lien entre les conséquences sémantiques et syntaxiques ?
Si on veut que nos démonstrations aboutissent à des résultats ayant du sens, il faut qu’ils correspondent aux conséquences sémantiques. Et à l’inverse, on souhaite qu’une conséquence sémantique puisse se démontrer mécaniquement. Le système de règles de démonstrations va être consciencieusement mis au point afin d’aboutir à l’équivalence entre les deux conséquences : $\mathcal{T}\models \phi$ si et seulement si $\mathcal{T} \vdash \phi$. Et en particulier, on veut qu’une formule soit une tautologie si et seulement si elle est prouvable sans hypothèse : $\models \phi$ ssi $\vdash \phi$.
On va distinguer trois familles de systèmes de démonstration différents pour le calcul des propositions :
- les systèmes axiomatiques,
- la déduction naturelle,
- le calcul des séquents.
Les systèmes axiomatiques
Les systèmes axiomatiques ou systèmes “à la Hilbert” reposent sur un petit nombre de vérités élémentaires, les axiomes, et sur des règles de construction qui préservent la vérité.
Les démonstrations obtenues sont concises mais très peu explicatives. Ça marche, mais on ne sait pas pourquoi, faute au manque de structure de ces preuves.
Exemple d’un système axiomatique reposant sur le système complet de connecteur $\set{\neg,\rightarrow}$ et comportant 3 axiomes pour une seule règle :
| Axiomes | ||
|---|---|---|
| $(1)\quad\phi\rightarrow (\psi\rightarrow\phi)$ | $(2)\quad(\phi\rightarrow (\psi\rightarrow\theta))\rightarrow ((\phi\rightarrow\psi)\rightarrow(\phi\rightarrow\theta))$ | $(3)\quad(\neg\psi\rightarrow \neg\phi) \rightarrow ((\neg \psi\rightarrow\phi)\rightarrow \psi)$ |
| Règle | ||
| modus ponens : de $\phi$ et $\phi\rightarrow \psi$ on déduit $\psi$ | ||
La déduction de $\phi$ à partir d'un ensemble de formules $\Gamma$ est une suite finie de formules $\langle \phi_1,\phi_2,\ldots,\phi_n\rangle$ telle que :
- chaque $\phi_i$ vérifie une des trois conditions suivantes :
- $\phi_i$ est un axiome,
- $\phi_i$ est une hypothèse ($\phi_i \in \Gamma$),
- $\phi_i$ est obtenue à partir de l’application de la règle du modus ponens à deux formules $\phi_j$ et $\phi_k$ telles que $j,k≤i$.
- $\phi_n=\phi$
Exemple de la démonstration de la formule $(\phi\rightarrow\phi)$ sans hypothèse :
$ \begin{array}{llr} (1)& (\phi\rightarrow ((\phi\rightarrow \phi)\rightarrow\phi))\rightarrow ((\phi\rightarrow (\phi\rightarrow \phi))\rightarrow(\phi\rightarrow\phi)) & \text{(axiome 2 avec } \psi = (\phi\rightarrow \phi) \text{ et }\theta = \phi )\\ (2)& \phi\rightarrow ((\phi\rightarrow \phi)\rightarrow\phi) & \text{(axiome 1 avec } \psi = (\phi\rightarrow \phi) )\\ (3)& (\phi\rightarrow (\phi\rightarrow \phi))\rightarrow(\phi\rightarrow\phi) & (\textit{modus ponens} \text{ (1) - (2))}\\ (4)& \phi\rightarrow (\phi\rightarrow \phi) & \text{(axiome 1 avec } \psi = \phi )\\ (5)& \phi\rightarrow\phi & (\textit{modus ponens} \text{ (3) - (4))} \end{array} $
On ne peut pas dire que la démonstration nous éclaire beaucoup sur la vérité de $\phi\rightarrow \phi$…
En conclusion, les systèmes à la Hilbert sont utiles pour démontrer des trucs mais pas pour étudier les démonstrations elles-mêmes.
La déduction naturelle
Un séquent, noté $\Gamma\vdash\phi$, est un couple où :
- $\Gamma$ est un ensemble fini de formules,
- $\phi$ est une formule.
Remarques :
- $\Gamma$ représente les hypothèses que l’on veut utiliser.
- $\phi$ est la conclusion du séquent, la formule à démontrer.
- $\vdash$ se lit “démontre” ou “prouve”.
- On écrit $\vdash\phi$ si $\phi$ se démontre sans hypothèse ($\Gamma=\emptyset $).
- Un séquent est prouvable s'il peut être obtenu par une application finie de règles de démonstration.
- Une formule $\phi$ est prouvable si le séquent $\vdash\phi$ est prouvable.
On écrit $\Gamma\nvdash\phi$ si $\Gamma\vdash\phi$ n’est pas prouvable.
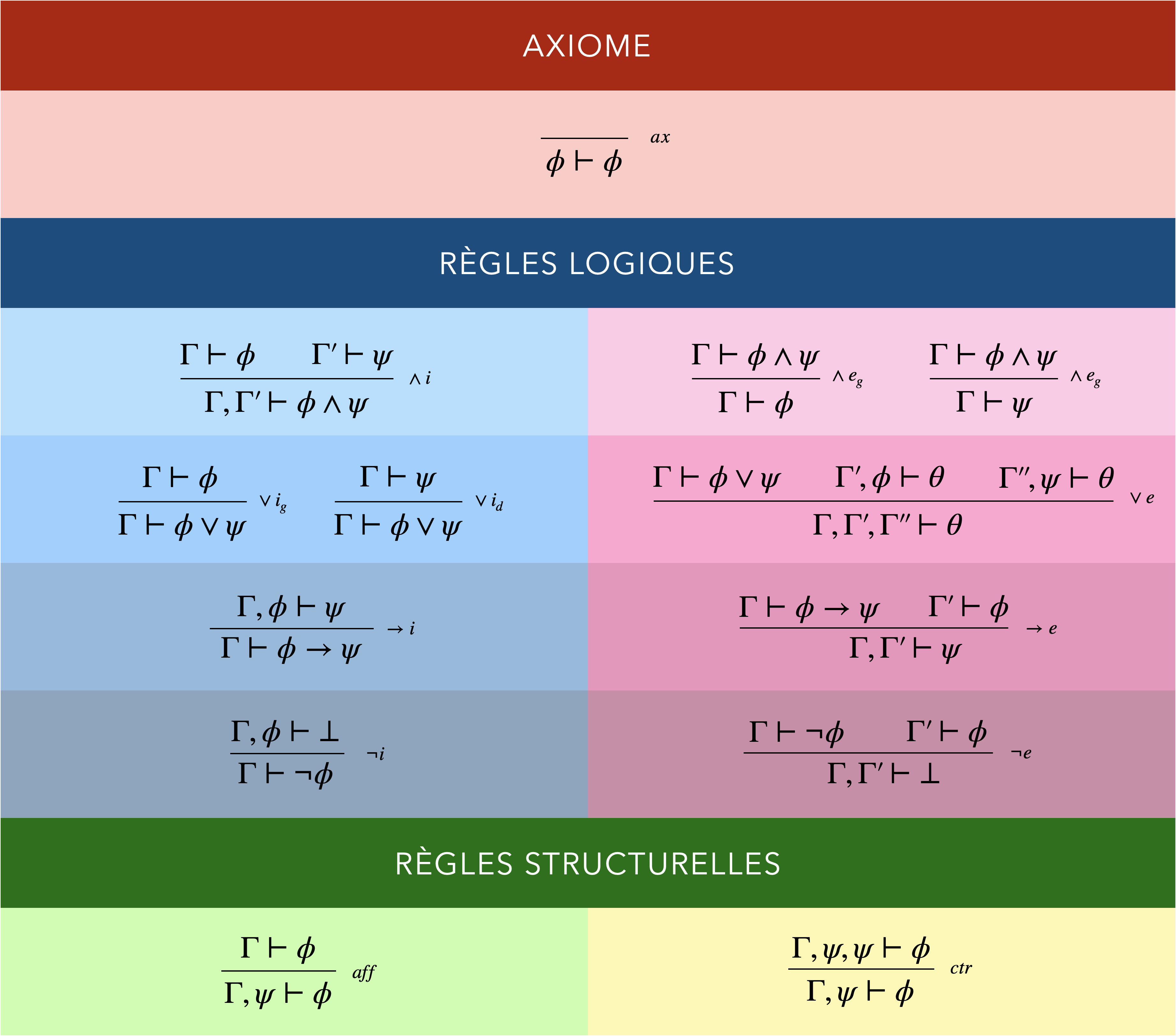
La règle est la brique de base de la démonstration. Une démonstration est ainsi un assemblage de règles généralement représenté sous forme d’arbre.
Chaque règle est composée :
- d’un ensemble de prémisses (de 0 à 3), chacune étant un séquent.
- d’un séquent conclusion.
- d’une barre horizontale qui sépare les deux (on identifie la règle à droite de la barre).
Pour chaque connecteur logique, on a deux types de règles :
- les règles d’introduction,
- et les règles d’élimination.
On va dans la suite considérer le système complet de connecteur $\set{\neg,\land,\lor,\rightarrow}$.
En dehors des axiomes représentés par le séquent $\phi \vdash\phi$, les règles peuvent être regroupées en deux catégories :
- les règles logiques (règles d’introduction et d’élimination des différents connecteurs).
- les règles structurelles permettant de manipuler les hypothèses ; l’affaiblissement permet d’ajouter de nouvelles hypothèses et la contraction permet de fusionner deux occurrences de la même hypothèse.
Logique minimale
Règles de la logique minimale :
- Axiome
$ \begin{prooftree} \AxiomC{} \RightLabel{$\;\scriptsize ax$} \UnaryInfC{$\phi\vdash\phi$} \end{prooftree} $
Un séquent dont la conclusion est aussi l'hypothèse est prouvable. - Introduction de la conjonction
$ \begin{prooftree} \AxiomC{$\Gamma\vdash\phi$} \AxiomC{$\Gamma'\vdash\psi$} \RightLabel{$\;\scriptsize \land i$} \BinaryInfC{$\Gamma,\Gamma' \vdash\phi\land\psi$} \end{prooftree} $
Si $\phi$ et $\psi$ sont prouvées, alors on prouve $\phi\land\psi$. - Élimination de la conjonction
$ \begin{array}{cc} \begin{prooftree} \AxiomC{$\Gamma\vdash\phi\land\psi$} \RightLabel{$\;\scriptsize \land e_g$} \UnaryInfC{$\Gamma \vdash\phi $} \end{prooftree} & \begin{prooftree} \AxiomC{$\Gamma\vdash\phi\land\psi$} \RightLabel{$\;\scriptsize \land e_d$} \UnaryInfC{$\Gamma \vdash\psi $} \end{prooftree} \end{array} $
De $\phi\land\psi$, on peut déduire $\phi$ et $\psi$. - Introduction de la disjonction
$ \begin{array}{cc} \begin{prooftree} \AxiomC{$\Gamma\vdash\phi$} \RightLabel{$\;\scriptsize \lor i_g$} \UnaryInfC{$\Gamma \vdash \phi\lor\psi $} \end{prooftree} & \begin{prooftree} \AxiomC{$\Gamma\vdash\psi$} \RightLabel{$\;\scriptsize \lor i_d$} \UnaryInfC{$\Gamma \vdash \phi\lor\phi $} \end{prooftree} \end{array} $
Si on a prouvé une formule, alors a fortiori, on a prouvé cette formule ou une autre. - Élimination de la disjonction
$ \begin{prooftree} \AxiomC{$\Gamma \vdash \phi \lor \psi$} \AxiomC{$\Gamma',\phi \vdash \theta$} \AxiomC{$\Gamma'',\psi \vdash \theta$} \RightLabel{$\;\scriptsize \lor e$} \TrinaryInfC{$\Gamma,\Gamma',\Gamma''\vdash \theta$} \end{prooftree} $
Si on a prouvé $\phi\lor\psi$, alors pour prouver $\theta$, il suffit de prouver $\theta$ en supposant $\phi$ ou prouver $\theta$ en supposant $\psi$. - Introduction de l'implication
$ \begin{prooftree} \AxiomC{$\Gamma,\phi\vdash\psi$} \RightLabel{$\;\scriptsize \rightarrow i$} \UnaryInfC{$\Gamma \vdash\phi\rightarrow\psi$} \end{prooftree} $
Pour prouver $\phi\rightarrow \psi$, il suffit de prouver $\psi$ avec $\phi$ ajoutée aux hypothèses. - Élimination de l'implication (modus ponens)
$ \begin{prooftree} \AxiomC{$\Gamma\vdash\phi\rightarrow\psi$} \AxiomC{$\Gamma'\vdash\phi$} \RightLabel{$\;\scriptsize \rightarrow e$} \BinaryInfC{$\Gamma,\Gamma'\vdash\psi$} \end{prooftree} $
Si on a prouvé $\phi$ et $\phi\rightarrow\psi$, alors on a prouvé $\psi$. - Introduction de la négation
$ \begin{prooftree} \AxiomC{$\Gamma,\phi \vdash\bot$} \RightLabel{$\;\scriptsize \neg i$} \UnaryInfC{$\Gamma\vdash\neg\phi$} \end{prooftree} $
Pour montrer $\neg\phi$, il suffit d'aboutir à une contradiction en supposant $\phi$. - Élimination de la négation
$ \begin{prooftree} \AxiomC{$\Gamma \vdash \neg\phi$} \AxiomC{$\Gamma' \vdash \phi$} \RightLabel{$\;\scriptsize \neg e$} \BinaryInfC{$\Gamma,\Gamma'\vdash \bot$} \end{prooftree} $
Si on a prouvé à la fois $\phi$ et $\neg\phi$, alors on a prouvé une contradiction. - Affaiblissement
$ \begin{prooftree} \AxiomC{$\Gamma \vdash \phi$} \RightLabel{$\;\scriptsize aff$} \UnaryInfC{$\Gamma,\psi\vdash \phi$} \end{prooftree} $
Si on peut prouver $\phi$ avec les hypothèses $\Gamma$, alors on peut prouver $\phi$ en ajoutant d'autres hypothèses à $\Gamma$ (il peut y avoir des hypothèses qui ne servent pas). - Contraction
$ \begin{prooftree} \AxiomC{$\Gamma,\psi,\psi \vdash \phi$} \RightLabel{$\;\scriptsize ctr$} \UnaryInfC{$\Gamma,\psi\vdash \phi$} \end{prooftree} $
L'ensemble d'hypothèses $\Gamma\cup\set{\psi,\psi}$ est le même que $\Gamma\cup\set{\psi}$.
Chaque règle peut être regardée comme un arbre simple lu de haut en bas et dont la racine est en bas (pour une fois). Le séquent conclusion est donc la racine et les prémisses sont les feuilles.
- L’axiome n’est qu’une racine.
- Les éliminations de la conjonction, les introductions de la disjonctions, l’introduction de l’implication, l’introduction de la négation, l’affaiblissement et la contraction sont des arbres à une racine et une feuille.
- l’introduction de la conjonction, l’élimination de l’implication et l’élimination de la négation sont des arbres à une racine et deux feuilles.
- l’élimination de la disjonction et un arbre à une racine et trois feuilles.
Pour construire une preuve, on va assembler ces arbres.
Une déduction (en logique minimale) dans le système de la déduction naturelle est un arbre fini dont les nœuds sont des séquents $\left(S_i\right)_{i≤k}$, et tel que pour chaque nœud $S_i$ de la déduction :
- $S_i$ est une feuille si et seulement si $S_i$ est un axiome,
- si $S_i$ n'est pas une feuille, alors l'arbre dont $S_i$ est la racine et les enfants de $S_i$ sont les feuilles est une instance de l'une des règles du tableau.
Une formule $\phi$ est déductible des hypothèses $\Gamma$ s’il existe une déduction dont la racine soit le séquent $\Delta\vdash\phi$ pour un ensemble d’hypothèses $\Delta \subseteq \Gamma$. On note alors $\Gamma\vdash_m \phi$.
Exemples de preuves :
Prouver que $(\phi\rightarrow (\psi\rightarrow\theta))\rightarrow ((\phi\rightarrow\psi)\rightarrow(\phi\rightarrow\theta))$ est bien un théorème du calcul des propositions revient à obtenir une déduction du séquent $\vdash_{\! m} \;(\phi\rightarrow (\psi\rightarrow\theta))\rightarrow ((\phi\rightarrow\psi)\rightarrow(\phi\rightarrow\theta)$ :
Preuve du séquent $\vdash_{\!m}\; \phi\rightarrow\neg\neg\phi$ :
Par contre, on ne peut pas prouver l’implication inverse avec les règles de la logique minimale ($\nvdash_{\!m} \neg\neg\phi\rightarrow\phi$). On ne peut donc pas éliminer les doubles négations (on verra plus loin qu’il manque la règle de l’absurdité classique pour y parvenir).
Montrons que $\vdash_{\!m} \,\neg\phi\leftrightarrow (\phi\rightarrow\bot)$ :
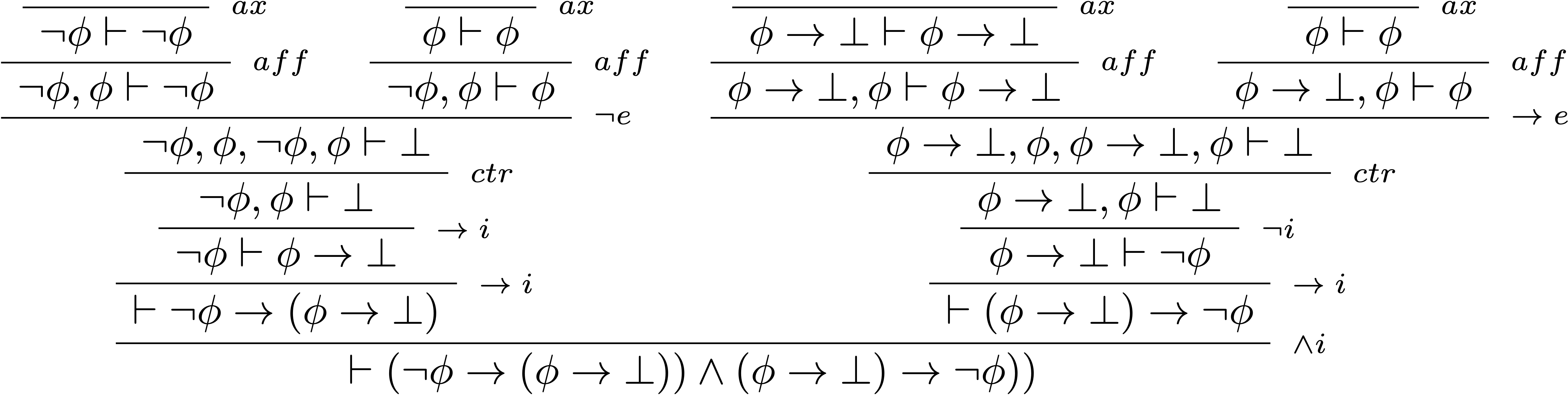
Rq : pour raccourcir les preuves, on va intégrer dorénavant les affaiblissements et contractions aux autres règles.
La notion de preuve telle qu’on l’a défini ne s’appuie que sur un enchaînement de règles pour aboutir à la conclusion. Il s’agit donc d’une conséquence syntaxique des formules en hypothèse.
De la même manière qu’on a défini l’équivalence sémantique à partir de la notion de conséquence sémantique, on va définir une équivalence au sens syntaxique à partir des séquents.
Deux formules $\phi$ et $\psi$ sont équivalentes pour la logique minimale si on a à la fois $\phi\vdash_{\!m}\psi$ et $\psi\vdash_{\!m}\phi$, et on écrit $\phi\equiv_m\psi$
Logique intuitionniste
Certains raisonnements ne sont pas possibles avec la logique minimale. On va enrichir le pouvoir expressif de notre système déductif grâce à de nouvelles règles. Ces règles concernent la contradiction $\bot$, et plus précisément son élimination.
Absurdité intuitionniste (ou élimination de la contradiction)
$
\begin{prooftree}
\AxiomC{$\Gamma\vdash\bot$}
\RightLabel{$\;\scriptsize \bot e_i$}
\UnaryInfC{$\Gamma\vdash\phi$}
\end{prooftree}
$
Si une contradiction découle d’un jeu d’hypothèses, alors n’importe quelle formule est démontrable avec ces mêms hypothèses.
On obtient ainsi un nouveau système déductif ; celui de la logique intuitionniste.
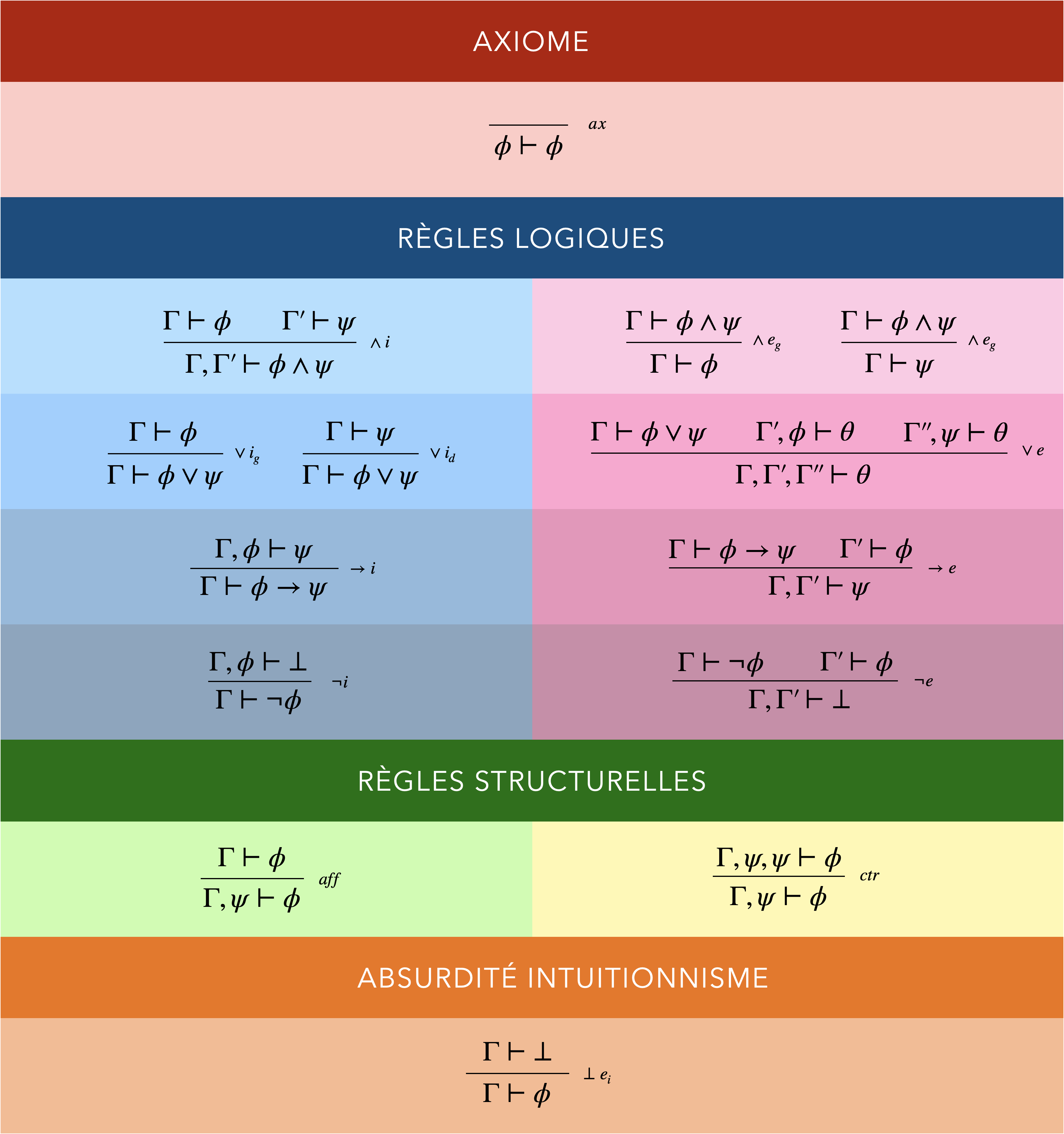
La règle de l’absurdité intuitionniste n’est pas démontrable dans le cadre de la logique minimale. Les déductions qui utilisent cette règle ne sont donc pas possibles en logique minimale. Il existe par conséquent des formules qui sont des théorèmes en logique intuitionniste (des séquents démontrables), mais restent non prouvables en logique minimale.
Deux formules $\phi$ et $\psi$ sont équivalentes pour la logique intuitionniste si on a à la fois $\phi\vdash_{\!i}\psi$ et $\psi\vdash_{\!i}\phi$, et on écrit $\phi\equiv_i\psi$.
La logique classique
Absurdité classique
$
\begin{prooftree}
\AxiomC{$\Gamma,\neg\phi\vdash\bot$}
\RightLabel{$\;\scriptsize \bot e_c$}
\UnaryInfC{$\Gamma\vdash\phi$}
\end{prooftree}
$
Si une contradiction découle d’un jeu d’hypothèse auquel on ajoute la négation d’une formule, alors la formule est démontrable à partir du jeu d’hypothèses de départ.
En ajoutant à la logique minimale non pas la règle de l’absurdité intuitionniste mais cette règle de l’absurdité classique, on obtient la logique classique.
L’absurdité classique n’est démontrable ni en logique minimale, ni en logique intuitionniste, alors que l’absurdité intuitionniste n’est qu’un cas particulier de l’absurdité classique.
Cela montre que la logique classique est un upgrade par rapport à la logique intuitionniste.
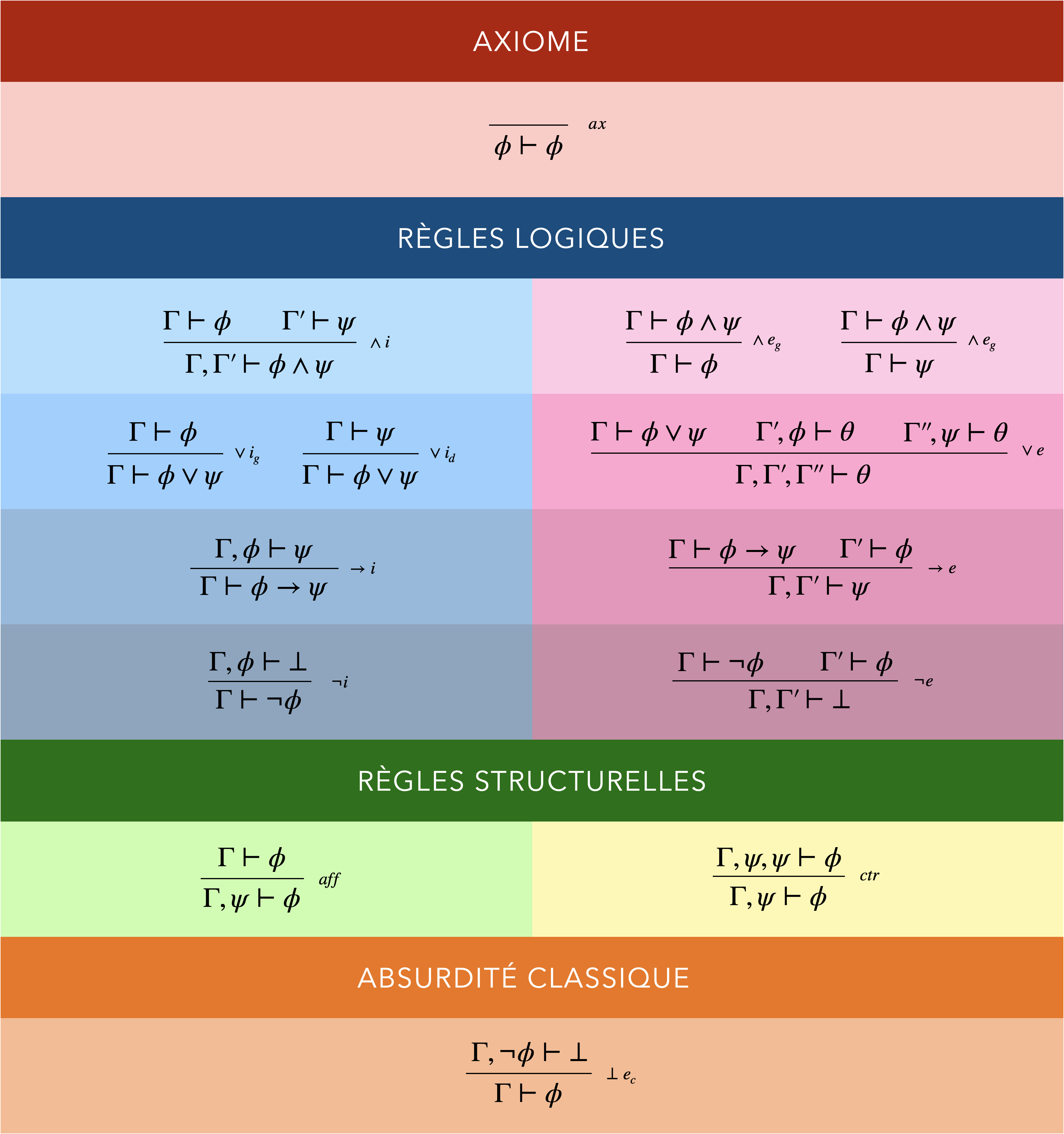
Des raisonnements comme la loi du tiers exclu ou l’élimination des doubles négations deviennent enfin démontrables (ils ne l’étaient pas en logique intuitionniste et a fortiori pas non plus en logique minimale).
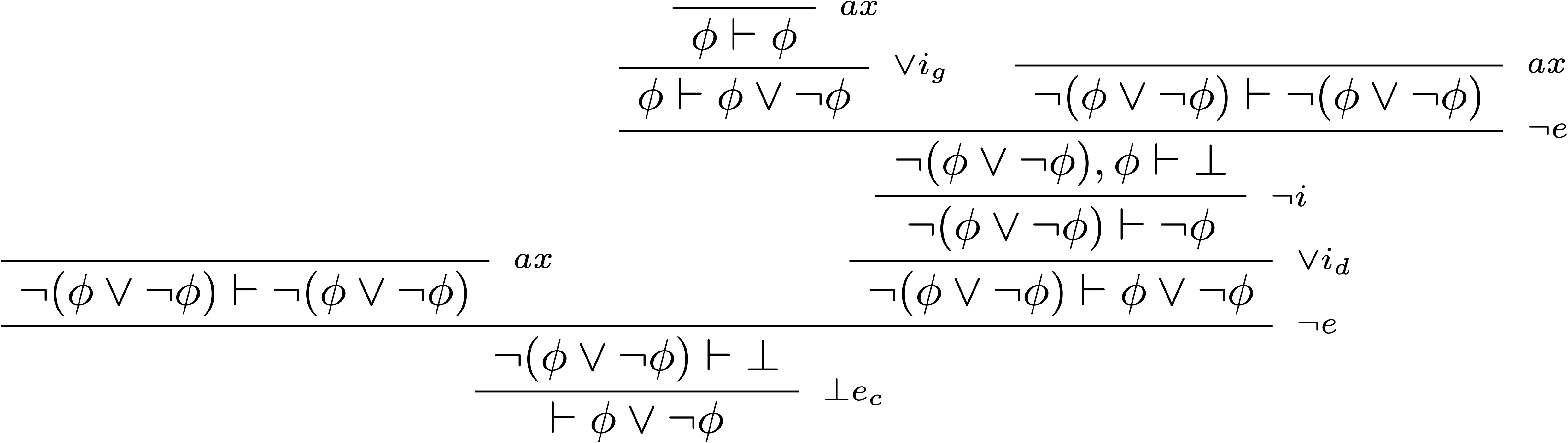
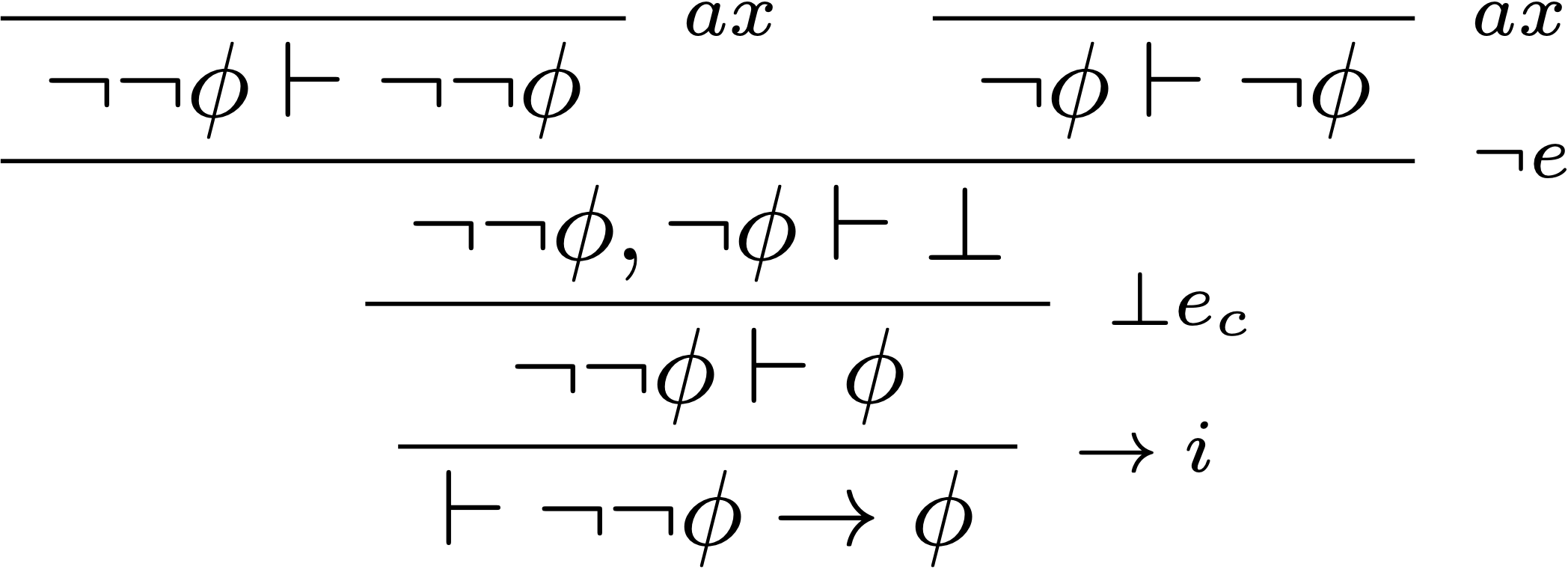
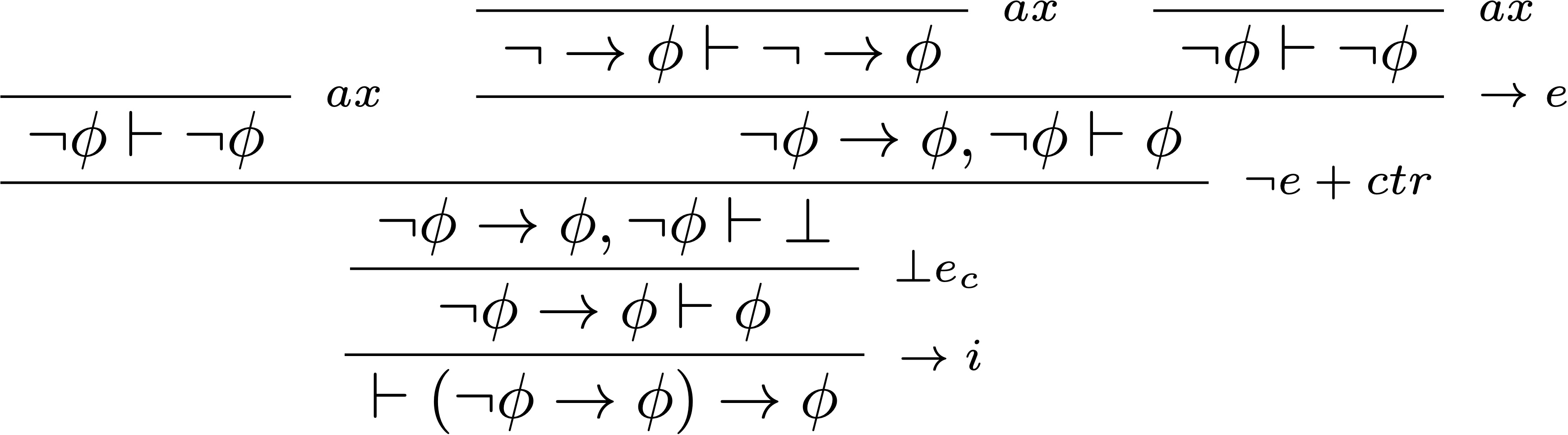
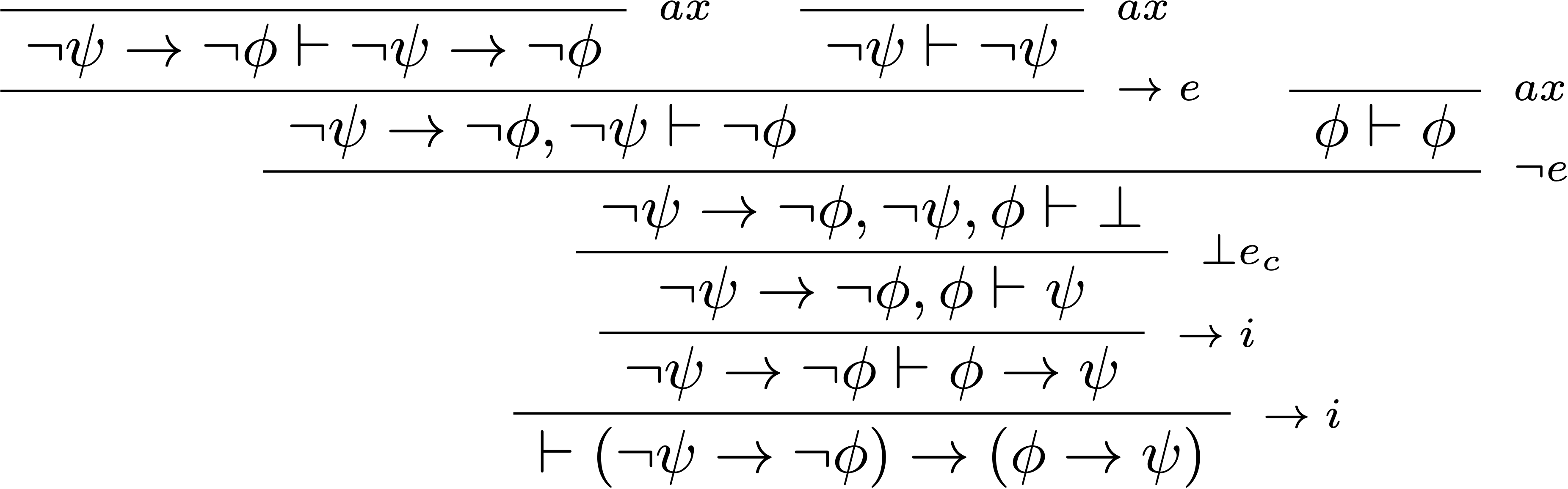
L’ajout de l’absurdité classique aux règles de la logique minimale n’est pas le seul chemin pour obtenir la logique classique. En utilisant chacun des quatre différents séquents que l’on vient de démontrer comme axiome, on peut augmenter soit la logique minimale, soit la logique intuitionniste en logique classique.
- logique classique = logique intuitionniste + principe du tiers exclu
- logique classique = logique intuitionniste + loi de Peirce
- logique classique = logique minimale + élimination des doubles négations
- logique classique = logique minimale + contraposition
Nous allons montré que les inclusions sont vérifiées dans les deux sens.
- Pour le sens $\supset$, c'est déjà fait.
En effet, on a démontré plus haut que chacun des axiomes ajoutés peut se démontrer en logique classique sans hypothèse supplémentaire. - Sens $\subset$ : il suffit de vérifier à chaque fois que la règle de l'absurde classique peut être obtenue à partir de la logique considérée à laquelle on a ajouté l'axiome.
- logique classique $\subset$ logique intuitionniste + principe du tiers exclu :
$$ \begin{prooftree} \AxiomC{} \RightLabel{$\scriptsize\;ax$} \UnaryInfC{$\color{#970E53}\vdash\phi\lor\neg\phi$} \AxiomC{} \RightLabel{$\scriptsize\;ax$} \UnaryInfC{$\phi\vdash\phi$} \AxiomC{$\Gamma,\neg\phi\vdash\bot$} \RightLabel{$\scriptsize\;\bot e_i$} \UnaryInfC{$\Gamma,\neg\phi\vdash\phi$} \RightLabel{$\scriptsize\;\lor e$} \TrinaryInfC{$\Gamma\vdash\phi$} \end{prooftree} $$ - logique classique $\subset$ logique intuitionniste + loi de Peirce :
$$ \begin{prooftree} \AxiomC{} \RightLabel{$\scriptsize\;ax$} \UnaryInfC{$\color{#970E53}\neg\phi\rightarrow\phi\vdash\phi$} \RightLabel{$\scriptsize\;\rightarrow i$} \UnaryInfC{$\vdash (\neg\phi\rightarrow\phi)\rightarrow\phi$} \AxiomC{$\Gamma,\neg\phi\vdash\bot$} \RightLabel{$\scriptsize\;\bot e_i$} \UnaryInfC{$\Gamma,\neg\phi\vdash\phi$} \RightLabel{$\scriptsize\;\rightarrow i$} \UnaryInfC{$\Gamma\vdash \neg\phi\rightarrow\phi$} \RightLabel{$\scriptsize\;\lor e$} \BinaryInfC{$\Gamma\vdash\phi$} \end{prooftree} $$ - logique classique $\subset$ logique minimale + élimination des doubles négations :
$$ \begin{prooftree} \AxiomC{} \RightLabel{$\scriptsize\;ax$} \UnaryInfC{$\color{#970E53}\vdash\neg\neg\phi\rightarrow\phi$} \AxiomC{$\Gamma,\neg\phi\vdash\bot$} \RightLabel{$\scriptsize\;\neg i$} \UnaryInfC{$\Gamma\vdash\neg\neg\phi$} \RightLabel{$\scriptsize\;\lor e$} \BinaryInfC{$\Gamma\vdash\phi$} \end{prooftree} $$ - logique classique $\subset$ logique minimale + contraposition
On va utiliser une instance de la contraposition où $\psi:=\phi$ et $\phi:=\neg\bot$ :
$$ \begin{prooftree} \AxiomC{} \RightLabel{$\scriptsize\;ax$} \UnaryInfC{$\color{#970E53}\neg\phi\rightarrow\neg\neg\bot\vdash\neg\bot\rightarrow\phi$} \RightLabel{$\scriptsize\;\rightarrow i$} \UnaryInfC{$\vdash (\neg\phi\rightarrow\neg\neg\bot)\rightarrow(\neg\bot\rightarrow\phi)$} \AxiomC{} \RightLabel{$\scriptsize\;ax$} \UnaryInfC{$\bot\vdash\bot$} \AxiomC{} \RightLabel{$\scriptsize\;ax$} \UnaryInfC{$\neg\bot\vdash\neg\bot$} \RightLabel{$\scriptsize\;\rightarrow e$} \BinaryInfC{$\bot,\neg\bot\vdash\bot$} \RightLabel{$\scriptsize\;\neg i$} \UnaryInfC{$\bot\vdash\neg\neg\bot$} \RightLabel{$\scriptsize\;\rightarrow i$} \UnaryInfC{$\vdash \bot\rightarrow\neg\neg\bot$} \AxiomC{$\Gamma,\neg\phi\vdash\bot$} \RightLabel{$\scriptsize\;\rightarrow e$} \BinaryInfC{$\Gamma,\neg\phi\vdash\neg\neg\bot$} \RightLabel{$\scriptsize\;\rightarrow i$} \UnaryInfC{$\Gamma\vdash\neg\phi\rightarrow\neg\neg\bot$} \RightLabel{$\scriptsize\;\rightarrow e$} \BinaryInfC{$\Gamma\vdash\neg\bot\rightarrow\phi$} \AxiomC{} \RightLabel{$\scriptsize\;ax$} \UnaryInfC{$\bot\vdash\bot$} \RightLabel{$\scriptsize\;\neg i$} \UnaryInfC{$\vdash\neg\bot$} \RightLabel{$\scriptsize\;\rightarrow e$} \BinaryInfC{$\Gamma\vdash\phi$} \end{prooftree} $$
- logique classique $\subset$ logique intuitionniste + principe du tiers exclu :
La logique intuitionniste, contrairement à la logique classique, vise à obtenir des preuves constructives. Établir la vérité de $\phi$ ne suffit pas, il faut la construire étape par étape. Or les raisonnements par l’absurde classique ne construisent pas réellement la vérité de $\phi$ puisqu’ils se contentent d’établir une contradiction mettant en jeu $\neg\phi$. De même, le tiers exclu nous affirme que $\phi=\psi\lor\neg\psi$ sans jamais établir la vérité de $\psi$ ou $\neg\psi$.
Exemple classique de l’utilisation du tiers exclu en mathématique :
prouvons qu’il existe un couple de nombres irrationnels $(a,b)$ ($a,b\in\mathbb{R}\setminus \mathbb{Q}$) tels que $a^b$ soit rationnel ($a^b\in\mathbb{Q}$).
Sachant que $\sqrt{2}$ est irrationnel, on distingue deux cas :
si $\sqrt{2}^\sqrt{2}$ est rationnel, alors on prend $a=b=\sqrt{2}$
si $\sqrt{2}^\sqrt{2}$ est irrationnel, alors on prend $a=\sqrt{2}^\sqrt{2}$ et $b=\sqrt{2}$ puisqu’ainsi $a^b=2$.
On a donc bien répondu à la question puisque d’après le principe du tiers exclu, on est dans un cas ou dans l’autre. Mais pour savoir laquelle des deux options est la bonne, il faudrait savoir si $\sqrt{2}^\sqrt{2}$ est rationnel ou non (et démontrer qu’il ne l’est pas est beaucoup plus lourd)…
En logique intuitionniste, si l’on a réussi à démontrer le séquent $\vdash_{\! i}\phi\lor\psi$, c’est qu’on a démontré un des deux séquents $\vdash_{\! i}\phi$ ou $\vdash_{\! i}\psi$. Il n’y a pas de vérité intermédiaire indéterminée.
Un autre grief contre la logique classique concerne l’implication matérielle : $\phi\rightarrow\psi$ est considérée comme vraie si $\neg\phi$ sans qu’on n’ait jamais eu à construire de lien entre $\phi$ et $\psi$. La philosophe Dorothy Edgington en a tiré une démonstration de l’existence de Dieu grâce à la formule suivante : si Dieu n’existe pas ($\neg G$), il n’est pas vrai que si je prie ($P$), alors mes prières seront entendues ($A$). L’affirmation ne semble pas choquante. Sous forme de formule, cela donne : $(\neg G)\rightarrow \neg(P\rightarrow A)$. La formule peut se réécrire en éliminant les implications : $G\lor\neg(\neg P \lor A)$. Et voilà maintenant le coup de grâce, sous la forme d’une deuxième formule : $\neg P$, “je ne prie pas”. Et si $P$ est faux, seul $G$ survit dans la formule principale ; “Dieu existe”.
Les règles de la logique classique permettent de faire coïncider les notions de conséquence syntaxique et de conséquence sémantique.
Correction de la logique classique :
Soient $\Gamma$ un ensemble fini de formules et $\phi$ une formule du calcul des propositions,
Si $\Gamma\vdash_{\!c}\phi$ alors $\Gamma\models\phi$
Une preuve étant une suite finie de séquent, on va procéder par induction sur la longueur de la preuve.
- Si la preuve a une longueur 1, le séquent ne peut être qu'un axiome de la forme $\phi\vdash\phi$.
Reste à montrer que $\phi\models\phi$ est vraie. Et c'est bien sûr le cas : par définition, $\phi\models\phi$ est vraie si $\phi$ est vraie dans chaque modèle où $\phi$ est vraie...
- On suppose maintenant la propriété vraie pour toutes les preuves de longueur $n$.
Une preuve de longueur $n+1$ est une preuve de longueur $n$ à laquelle on ajoute un séquent qui est soit un axiome (on revient au cas précédent), soit une des règles.
Il faut montrer que les règles ont été judicieusement choisies pour "conserver" la notion de conséquence sémantique entre els prémisses et la conclusion.
Ici, les prémisses sont bien des conséquences sémantiques par application de l'hypothèse d'induction (elles correspondent à des séquents de longueur $≤n$).
On doit maintenant vérifier sur chaque règle que le séquent conclusion est une conséquence sémantique des prémisses.
Montrons-le pour la règle d'élimination de l'implication $ \begin{prooftree} \AxiomC{$\Gamma\vdash\phi\rightarrow\psi$} \AxiomC{$\Gamma'\vdash\phi$} \RightLabel{$\scriptsize\;\rightarrow e$} \BinaryInfC{$\Gamma,\Gamma'\vdash\psi$} \end{prooftree} $ :
Par hypothèse d'induction, on sait que $\Gamma\models\phi\rightarrow\psi$ et $\Gamma'\models\phi$. Donc dans les modèles de $\Gamma \cup \Gamma'$ (ensemble des modèles où les formules de $\Gamma$ et $\Gamma'$ sont vraies simultanément), à la fois $\phi\rightarrow\psi$ et $\phi$ sont vérifiées. Et comme lorsque $\phi$ est vraie, $\phi\rightarrow\psi$ n'est vraie que si $\psi$ est vraie, il en résulte que $\psi$ est vraie dans ces modèles : $\Gamma,\Gamma'\models\psi$.
On peut montrer de manière équivalente que cela marche pour chaque règle...
Une conséquence de la correction de la logique classique est que pour toute théorie finie $\Gamma$ et pour tout modèle $\mathcal{M}$ de cette théorie, si une formule est démontrable à partir des hypothèses $\Gamma$, alors elle est vraie dans $\mathcal{M}$.
Tout ce que l’on peut déduire syntaxiquement d’une théorie est vrai dans un modèle quelconque de cette théorie.
Complétude de la logique classique :
Soient $\Gamma$ un ensemble fini de formules et $\phi$ une formule du calcul des propositions,
Si $\Gamma\models\phi$ alors $\Gamma\vdash_{\!c}\phi$
Soit $\phi$, une formule quelconque du calcul des propositions dont les variables sont parmis $\set{P_1,\ldots,P_n}$, et $\mathcal{M}$, un modèle possible de $\phi$. On note :
- $P_i^\mathcal{M} = P_i$ si $P_i$ est vraie dans $\mathcal{M}$,
- $P_i^\mathcal{M} = \neg P_i$ sinon.
On pose également :
- $\phi^\mathcal{M} = \phi$ si $\mathcal{M}\models\phi$,
- $\phi^\mathcal{M} = \neg\phi$ sinon.
Par induction sur la hauteur de $\phi$ on veut montrer le résultat suivant : $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\phi^{\mathcal{M}}$
- si $ht(\phi)=0$, $\phi$ est une variable propositionnelle $P_i$ et il est alors immédiat que $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}P_i^{\mathcal{M}}$
- si $ht(\phi)=n+1$, alors on a une des possibilités suivantes : $\phi=\neg\psi$, $\phi=\psi_1\rightarrow\psi_2$, $\phi=\psi_1\lor\psi_2$ ou $\phi=\psi_1\land\psi_2$.
Chaque $\psi$, de hauteur $n$, respecte par hypothèse la propriété et on doit montrer dans chaque cas que cela implique le même respect de la propriété pour $\phi$.Prenons par exemple le cas $\phi=\psi_1\rightarrow\psi_2$ pour voir le type de raisonnement qu’il faut mener :
- Si $\mathcal{M}\not\models\psi_1$, alors $\mathcal{M}\models\phi$ et donc $\phi^\mathcal{M}=\phi$, et $\psi_1^\mathcal{M}=\neg\psi_1$.
Par hypothèse d'induction, $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\neg\psi_1$
Considérons la règle suivante :
- Si $\mathcal{M}\not\models\psi_1$, alors $\mathcal{M}\models\phi$ et donc $\phi^\mathcal{M}=\phi$, et $\psi_1^\mathcal{M}=\neg\psi_1$.
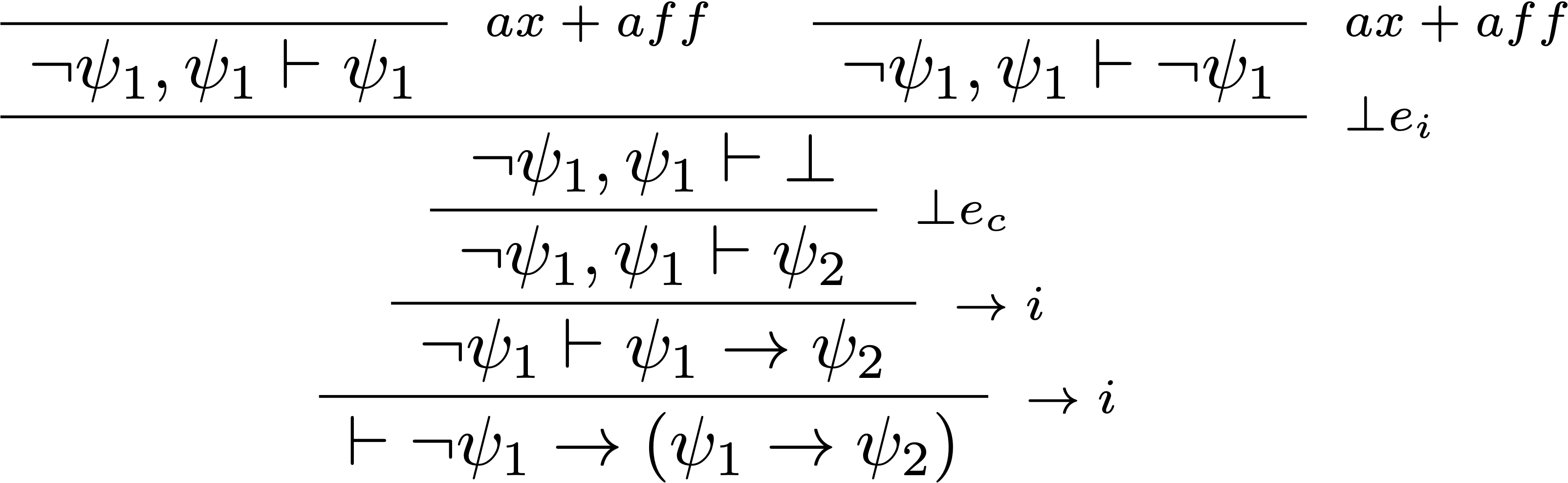
- L'utilisation de cette règle et du modus ponens permet d'obtenir : $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\psi_1\rightarrow\psi_2$, ce qui est bien ce que l'on voulait montrer puisque $\psi_1\rightarrow\psi_2=\phi^\mathcal{M}$
- Si $\mathcal{M}\models\psi_1$, alors :
- Si $\mathcal{M}\models\psi_2$, alors $\mathcal{M}\models\phi$ et donc $\phi^\mathcal{M}=\phi$, $\psi_1^\mathcal{M}=\psi_1$ et $\psi_2^\mathcal{M}=\psi_2$.
Par hypothèse d'induction, on a : $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\psi_1^\mathcal{M}$ et $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\psi_2^\mathcal{M}$
C'est-à-dire : $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\psi_1$ et $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\psi_2$
De $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\psi_2$, on déduit par affaiblissement $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}},\psi_1 \vdash_{\!c}\psi_2$, puis par introduction de l'implication : $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\psi_1 \rightarrow\psi_2$ - Si $\mathcal{M}\not\models\psi_2$, alors $\mathcal{M}\not\models\phi$ et donc $\phi^\mathcal{M}=\neg\phi$, $\psi_1^\mathcal{M}=\psi_1$ et $\psi_2^\mathcal{M}=\neg\psi_2$.
Par hypothèse d'induction, on a : $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\psi_1^\mathcal{M}$ et $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\psi_2^\mathcal{M}$
C'est-à-dire : $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\psi_1$ et $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\neg\psi_2$
On en déduit : $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\psi_1\land\neg\psi_2$.
Considérons la règle suivante :
- Si $\mathcal{M}\models\psi_2$, alors $\mathcal{M}\models\phi$ et donc $\phi^\mathcal{M}=\phi$, $\psi_1^\mathcal{M}=\psi_1$ et $\psi_2^\mathcal{M}=\psi_2$.
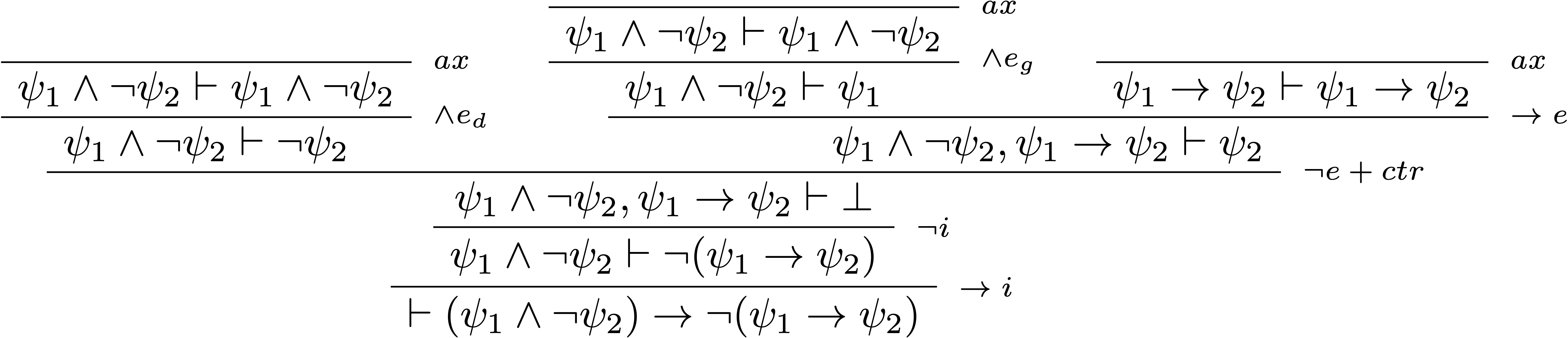
- On applique ensuite la règle du modus ponens pour obtenir $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\neg(\psi_1\rightarrow\psi_2)$ qui est bien le résultat recherché.
Supposons qu’on ait passé en revue tous les autres cas pour finir de montrer que $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\phi^{\mathcal{M}}$.
Nous allons maintenant prouver que pour toute formule $\phi$, si $\phi$ est une tautologie, alors $\phi$ est un théorème de la logique classique.
Soit $\phi$, une formule quelconque du calcul des propositions dont les variables sont $P_1,\ldots,P_n$. Et soit $\mathcal{M}$ un modèle possible de $\phi$. On a montré que $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\phi^{\mathcal{M}}$. Or $\mathcal{M}\models\phi$ est vérifié, donc $\phi^\mathcal{M}=\phi$. D’où $\set{P_1^{\mathcal{M}},\ldots,P_n^{\mathcal{M}}} \vdash_{\!c}\phi$.
Si $\phi$ est une tautologie, ce résultat est valable pour n’importe quel modèle. Choisissons les modèles $\mathcal{M}$ et $\mathcal{M’}$ qui distribuent les mêmes valeurs de vérité pour toutes les variables $P_i$ sauf $P_n$. $\mathcal{M}\models P_n$ alors que $\mathcal{M’}\models \neg P_n$.
On a à la fois $\set{P_1^{\mathcal{M}},\ldots,P_{n-1}^{\mathcal{M}},P_n^{\mathcal{M}}} \vdash_{\!c}\phi$ et $\set{P_1^{\mathcal{M’}},\ldots,P_{n-1}^{\mathcal{M’}},P_n^{\mathcal{M’}}} \vdash_{\!c}\phi$.
D’où $\set{P_1^{\mathcal{M}},\ldots,P_{n-1}^{\mathcal{M}},P_n} \vdash_{\!c}\phi$ et $\set{P_1^{\mathcal{M}},\ldots,P_{n-1}^{\mathcal{M}},\neg P_n} \vdash_{\!c}\phi$ qu’on peut aussi écrire $\set{P_1^{\mathcal{M}},\ldots,P_{n-1}^{\mathcal{M}}},P_n \vdash_{\!c}\phi$ et $\set{P_1^{\mathcal{M}},\ldots,P_{n-1}^{\mathcal{M}}},\neg P_n \vdash_{\!c}\phi$.
Construisons la règle suivante en appliquant le tiers exclu :
Et en dernière étape, on obtient $P_1\vdash_{\!c}\phi$ et $\neg P_1\vdash_{\!c}\phi$. D'où l'on déduit $\vdash_{\!c}\phi$ par application du tiers exclu.
Nous avons donc bien réussi à prouver que $\models\phi$ implique $\vdash_{\!c}\phi$.
Il ne nous reste plus qu’à montrer que pour toute formule $\phi$ et pour tout ensemble fini d’hypothèses $\Gamma=\set{\psi_1,\ldots,\psi_k}$, $\Gamma\models\phi$ implique $\Gamma\vdash_{\!c}\phi$.
Il apparait immédiatement que $\Gamma\models\phi$ si et seulement si $\models(\psi_1\land\psi_2\land\ldots\land\psi_k)\rightarrow\phi $.
Le résultat précédent sur les tautologies nous permet de déduire que $\vdash_{\!c}(\psi_1\land\psi_2\land\ldots\land\psi_k)\rightarrow \phi$.
Il est évident par ailleurs que $\Gamma\vdash_{\!c}(\psi_1\land\psi_2\land\ldots\land\psi_k)$.
Par modus ponens, on obtient donc $\Gamma\vdash_{\!c}\phi$.
De façon informelle, la correction stipule que toute formule prouvable est vraie, alors que la complétude, de son côté, affirme que toutes les formules vraies sont prouvables.
Et dit autrement encore, on peut prouver toute la vérité (complétude) et rien que la vérité (correction).
Corollaire :
$\models\phi$ ssi $\vdash_{\!c}\phi$
Toute tautologie est démontrable sans utiliser d’hypothèse et à l’inverse, toute formule démontrable sans hypothèse est une tautologie.
Corollaire :
Soient $\phi$ et $\psi$ deux formules du calcul des propositions,
$\Gamma\equiv\psi$ ssi $\Gamma\equiv_c\psi$
On a montré finalement que la sémantique du calcul des propositions correspond à la logique classique. On peut d’ailleurs parler de “sémantique classique”. Mais qu’en est-il de la logique intuitionniste ? Peut-on définir une sémantique qui lui soit adaptée afin d’obtenir un théorème de complétude pour la logique intuitionniste ?
Oui, grâce aux modèles de Kripke.
Les modèles de Kripke du calcul des propositions intuitionniste
On a vu qu’une formule est démontrable en logique classique si et seulement si elle est vraie dans tous les modèles (classiques) possibles. On va aboutir à une proposition similaire grâce aux modèles de Kripke : une formule est démontrable en logique intuitionniste si et seulement si elle est réalisée dans tous les modèles de Kripke possibles.
Soit $\set{P_1,\ldots,P_k}$ un ensemble de variables propositionnelles.
$\mathcal{K}=(\mathcal{T}_\mathcal{K},\Vdash)$ est un modèle de Kripke arborescent fini sur les variables $P_1,\ldots,P_k$ si :
- $\mathcal{T}_\mathcal{K}$ est un arbre fini dont la relation d'ancestralité entre deux nœuds est noté $\alpha≤\beta$ ($\alpha$ est un ancêtre de $\beta$).
- $\Vdash$ est une relation binaire appelée relation de forcing entre les nœuds de $\mathcal{T}_\mathcal{K}$ et les variables propositionnelles qui vérifie :
- pour tout nœud $\alpha$ : $\alpha\not\Vdash\bot$
- pour tout nœud $\alpha$, $\beta$ et variable propositionnelle $P_i$, si à la fois $\alpha≤\beta$ et $\alpha\Vdash P_i$ alors on a $\beta\Vdash P_i$.
Un modèle de Kripke avec un seul nœud peut être vu comme un modèle de la logique classique car les conditions de la relations de forcing ($\Vdash$) sont alors identiques à celles de la relation de vérité sémantique ($\models$).
La relation de forcing fait en sorte que si une formule est vraie dans un nœud (qui représente un monde, comme on le verra en logique modale), alors elle reste vraie dans tous les nœuds accessibles depuis le nœud de départ (tous les mondes accessibles).
Soit $\mathcal{K}=(\mathcal{T}_\mathcal{K},\Vdash)$ un modèle de Kripke arborescent fini sur les variables $P_1,\ldots,P_k$, $\alpha$ un nœud de $\mathcal{T}_\mathcal{K}$ et $\phi$, $\psi$ des formules du calcul des propositions dont les variables sont parmi $\set{P_1,\ldots,P_k}$,
- $\alpha\Vdash \phi\land\psi$ ssi $\alpha\Vdash\phi$ et $\alpha\Vdash\psi$
- $\alpha\Vdash \phi\lor\psi$ ssi $\alpha\Vdash\phi$ ou $\alpha\Vdash\psi$
- $\alpha\Vdash \phi\rightarrow\psi$ ssi pour tout nœud $\beta$ de $\mathcal{T}_\mathcal{K}$ tel que $\alpha≤\beta$, si $\beta\Vdash\phi$ alors $\beta\Vdash\psi$.
On cherche ici à construire explicitement la vérité de $\psi$ à partir de celle de $\phi$ (alors qu'en logique classique, l'établissement de la vérité de $\phi$ n'est pas nécessaire puisque l'implication est considérée comme vraie soit par l'absence de $\phi$, soit par la présence de $\psi$). - $\alpha\Vdash \neg\phi$ ssi pour tout nœud $\beta$ de $\mathcal{T}_\mathcal{K}$ tel que $\alpha≤\beta$, $\beta\not\Vdash\phi$.
Dit autrement, aucun nœud ne force le faux.
En effet, la négation $\neg\phi$ est interprétée ici comme la formule $\phi\rightarrow\bot$. La définition de la relation de forcing de l'implication dit que : $\alpha\Vdash\phi\rightarrow\bot$ ssi pour tout nœud $\beta$ de $\mathcal{T}_\mathcal{K}$ tel que $\alpha≤\beta$, si $\beta\Vdash\phi$ alors $\beta\Vdash\bot$. Or la condition $\beta\Vdash\bot$ est interdite par définition des modèles de la logique intuitionniste, donc $\beta\Vdash\bot$ n'est satisfait nulle part. D'où $\beta\not\Vdash\phi$.
Voilà un exemple de modèle de Kripke sur les variables $P$, $Q$, $R$.
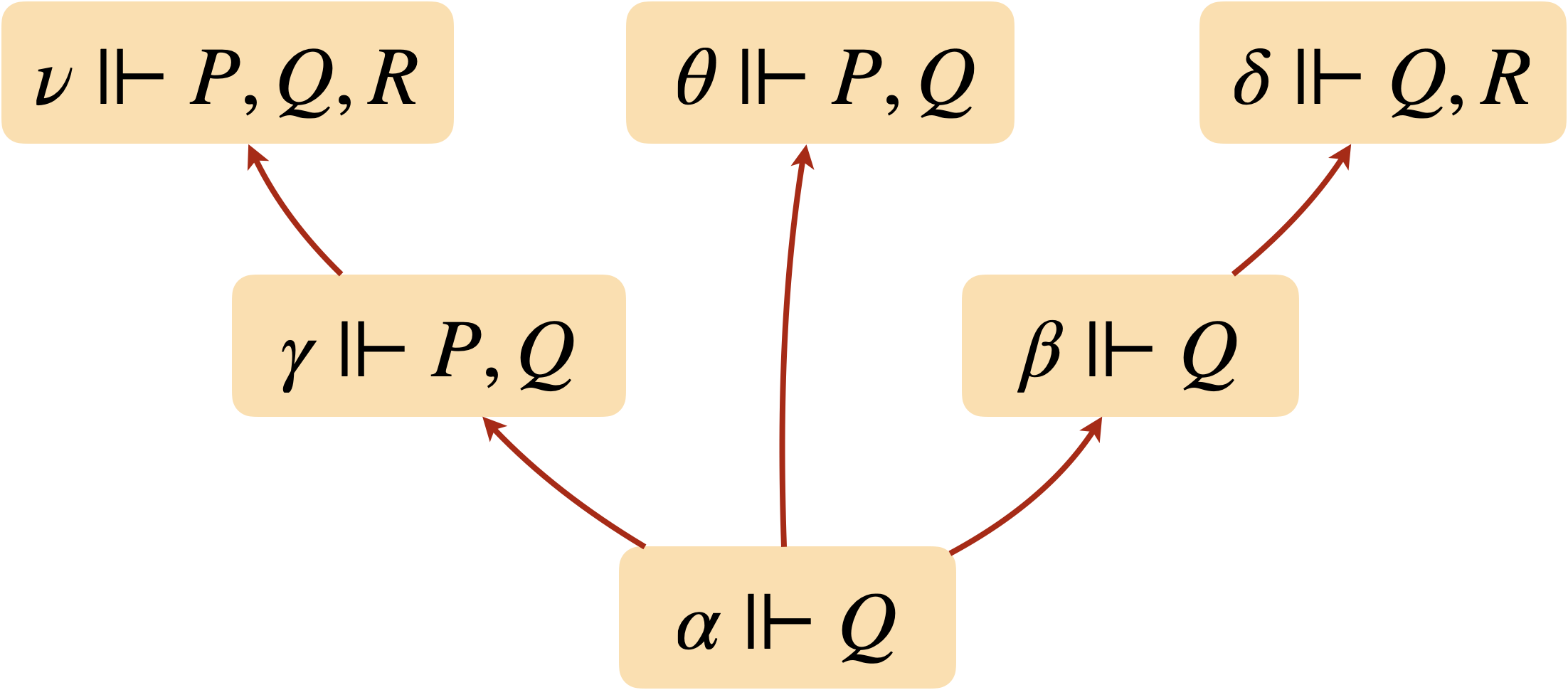 On y trouve les relations de forcing suivantes :
On y trouve les relations de forcing suivantes :
- $\theta\Vdash Q\land P$ mais $\beta\not\Vdash Q\land P$
- $\alpha\Vdash P\rightarrow Q$ mais $\alpha\not\Vdash Q\rightarrow P$
- $\beta\Vdash\neg P$ mais $\alpha\not\Vdash\neg P$
- $\alpha\not\Vdash P$, $\alpha\not\Vdash \neg P$ et $\alpha\not\Vdash \neg\neg P$
Soit $\mathcal{K}=(\mathcal{T}_\mathcal{K},\Vdash)$ un modèle de Kripke arborescent fini sur les variables $P_1,\ldots,P_k$, $\alpha$ un nœud de $\mathcal{T}_\mathcal{K}$, $\phi$ une formule et $\Gamma$ un ensemble fini de formules dont les variables sont parmi $\set{P_1,\ldots,P_k}$,
- $\alpha\Vdash \Gamma$ ssi $\alpha\Vdash\phi$ pour toute formule de $\Gamma$.
- $\phi$ (respectivement $\Gamma)$ est réalisée dans $\mathcal{K}$ si pour tout nœud $\alpha$ de $\mathcal{T}_\mathcal{K}$, $\alpha\Vdash\phi$ (respectivement $\alpha\Vdash\Gamma$).
- $\phi$ est une conséquence intuitionniste de $\Gamma$, noté $\Gamma\Vdash_i\phi$, ssi pour tout modèle de Kripke $\mathcal{K}=(\mathcal{T}_\mathcal{K},\Vdash)$ et tout nœud $\alpha$ si $\alpha\Vdash\Gamma$ alors $\alpha\Vdash\phi$.
En particulier, on note $\Vdash_i \phi$ si $\phi$ est réalisée dans tout modèle de Kripke.
 Ce modèle ne réalise ni le tiers exclu $(P\lor\neg P)$, ni l’élimination des doubles négations $(\neg\neg P\rightarrow P)$.
Ce modèle ne réalise ni le tiers exclu $(P\lor\neg P)$, ni l’élimination des doubles négations $(\neg\neg P\rightarrow P)$.
En effet :
-
$\alpha \not\Vdash P$ par définition et $\alpha\not\Vdash \neg P$ puisque $\alpha≤\beta$ et $\beta\Vdash P$. Donc $\alpha\not\Vdash P\lor\neg P$.
-
$\alpha\not\Vdash\neg P$ et $\beta\not\Vdash\neg P$ d’où $\alpha\Vdash \neg\neg P$ et $\beta\Vdash \neg\neg P$. D’où $\beta\Vdash\neg\neg P\rightarrow P$ et $\alpha\not\Vdash\neg\neg P\rightarrow P$ (puisque $\alpha \not\Vdash P$).
Cela permet de constater l’adaptation des modèles de Kripke à la logique intuitionniste ; il peut exister des modèles où ni $\phi$, ni $\neg\phi$ ne sont établis comme vrais.
Correction et complétude de la logique intuitionniste :
Soient $\Gamma$ un ensemble fini de formules et $\phi$ une formule du calcul des propositions,
$\Gamma\Vdash_i\phi$ ssi $\Gamma\vdash_{\!i} \phi$
Corollaire :
$\Vdash_i\phi$ ssi $\vdash_{\!i} \phi$
En abandonnant la condition “pour tout nœud $\alpha$ : $\alpha\not\Vdash\bot$” on obtient le modèle de Kripke adaptée à la logique minimale.
La condition de forcing de la négation devient alors $\alpha\Vdash\neg\phi$ ssi $\alpha\Vdash\phi\rightarrow\bot$ (pour tout nœud $\beta$ de $\mathcal{T}_\mathcal{K}$ tel que $\alpha≤\beta$, si $\beta\Vdash\phi$ alors $\beta\Vdash\bot$).
On obtient cette fois-ci :
Correction et complétude de la logique minimale :
Soient $\Gamma$ un ensemble fini de formules et $\phi$ une formule du calcul des propositions,
$\Gamma\Vdash_m\phi$ ssi $\Gamma\vdash_{\!m} \phi$
D’où découle $\Vdash_m\phi$ ssi $\vdash_{\!m} \phi$
 Dans ce modèle de Kripke de la logique minimale, $\neg\neg(\neg\neg P\rightarrow P)$ n’est pas réalisée.
Dans ce modèle de Kripke de la logique minimale, $\neg\neg(\neg\neg P\rightarrow P)$ n’est pas réalisée.
En effet, $\beta\not\Vdash P$ par définition, d’où $\beta\Vdash \neg P$. Mais on a également $\beta\Vdash\neg\neg P$ puisque $\beta\Vdash \bot$. Mais alors $\beta\not\Vdash \neg\neg P\rightarrow P$. Par conséquent $\beta\Vdash\neg(\neg\neg P\rightarrow P)$ et toujours à cause du fait que $\beta\Vdash \bot$, on obtient $\beta\Vdash \neg\neg(\neg\neg P\rightarrow P)$.
$\alpha\not\Vdash P$ et $\beta\not\Vdash P$ par définition, d’où $\beta\Vdash \neg P$. Mais $\alpha\not\Vdash \neg\neg P$ puisque $\alpha\not\Vdash\bot$. On a aussi $\alpha\not\Vdash\neg\neg P\rightarrow P$ puisque $\beta\Vdash \neg\neg P$ et $\beta\not\Vdash P$. Par conséquent, $\alpha\Vdash \neg(\neg\neg P\rightarrow P)$ puisqu’à la fois $\alpha\not\Vdash\neg\neg P \rightarrow P$ et $\beta\not\Vdash \neg\neg P\rightarrow P$. D’où $\alpha\not\Vdash\neg\neg(\neg\neg P\rightarrow P)$ puisqu’à la fois $\alpha\Vdash\neg(\neg\neg P \rightarrow P)$ et $\alpha\not\Vdash\bot$.
Il existe donc un nœud du modèle qui ne force pas la formule $\neg\neg(\neg\neg P\rightarrow P)$. Le théorème de complétude de la logique minimale nous dit alors que $\neg\neg(\neg\neg P\rightarrow P)$ n’est pas un théorème de la logique minimale.
Or on a montré que cette formule était un théorème de la logique intuitionniste. Le séquent $\vdash\neg\neg(\neg\neg P\rightarrow P)$ est donc prouvable en logique intuitionniste mais pas en logique minimale. Cela prouve que la logique minimale forme un sous-ensemble strict de la logique intuitionniste, elle-même strictement inclue dans la logique classique.
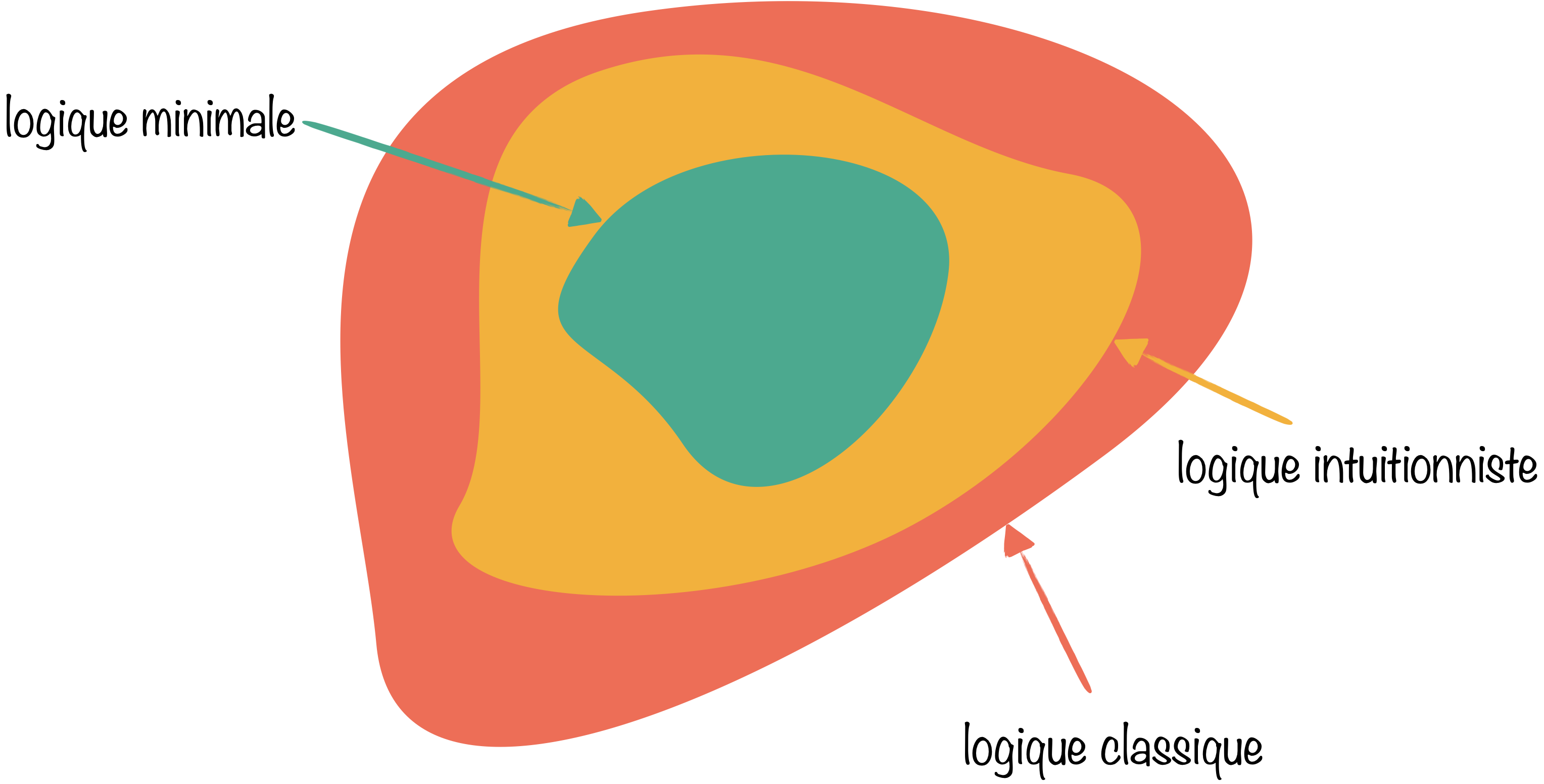
Le calcul des séquents
Comme la déduction naturelle, le calcul des séquents a été mis au point par Gerhard Gentzen. Son but est de mettre encore mieux en lumière les propriétés mathématiques de la notion de démonstration.
Les différences principales avec la déduction naturelle sont que la partie droite des séquents n’est plus une seule formule conclusion mais un ensemble fini de formules, et les règles d’élimination sont remplacées par des règles d’introduction à gauche afin de rendre le système de démonstration symétrique.
Un séquent (noté $\Gamma\vdash\Delta$) est un couple où :
- $\Gamma$ est un ensemble fini de formules, appelé la partie gauche du séquent,
- $\Delta$ est également un ensemble fini de formules, appelé la partie droite du séquent.
Intuitivement, un séquent $\Gamma\vdash\Delta$ où $\Gamma=\set{\phi_1,\ldots,\phi_n}$ et $\Delta=\set{\psi_1,\ldots,\psi_k}$ est interprété comme $\bigwedge_{1≤i≤n}\phi_i \vdash \bigvee_{1≤j≤k} \psi_j$. Une conjonction d’hypothèses prouve une disjonction de conclusions.
La conjonction vide d’hypothèse est interprété comme le vrai, alors que la disjonction vide de conclusion est interprétée comme le faux.
$\vdash\Delta$ signifie donc $(\psi_1\lor\psi_2\lor\ldots\lor\psi_k)$, alors que le séquent $\Gamma\vdash$ signifie $(\phi_1\land\phi_2\land\ldots\land\phi_n)\rightarrow\bot$, c’est-à-dire $\neg(\phi_1\land\phi_2\land\ldots\land\phi_n)$.
Enfin $\vdash$, qui signifie “vrai implique faux”, est interprété comme l’absurde (il correspond au séquent $\vdash\bot$ de la déduction naturelle).
Les règles du calcul des séquents sont très proches de celles de la déduction naturelle.
D’un ensemble de prémisses (0, 1 ou 2), on déduit un séquent conclusion.
Les règles d’introduction sont conservées, mais elles deviennent des règles d’introduction à droite. Les règles d’élimination deviennent, elles, des règles d’introduction à gauche.
Les règles structurelles sont symétrisées et on ajoute un axiome ainsi qu’une nouvelle règle, la règle de coupure :
En déduction naturelle, cela correspond aux deux prémisses $\Gamma\vdash\phi$ et $\phi\vdash\psi$ desquels on déduit $\Gamma\vdash\psi$.
La règle de coupure est souvent utilisée dans les preuves pour simplifier la déduction en introduisant des lemmes ou des théorèmes intermédiaires.
Étant donné qu’il n’y a plus de règles d’élimination, c’est la règle de coupure qui permet de rétablir la transitivité dans les déductions.

L’affaiblissement à droite reflète l’idée que si on a une preuve que quelque chose est vrai à partir d’un ensemble de prémisses, ajouter une conclusion supplémentaire comme possibilité n’enlève rien à la validité de cette preuve.
En remplaçant $\Delta$ par $\emptyset$, on retrouve la règle d’absurdité intuitionniste.
Les deux formules précédentes se ressemblent fortement mais seule la première est prouvable en logique intuitionniste.
Les deux preuves en calcul des séquents sont quasiment les mêmes, mais l’ordre d’introduction des négations est inversé (gauche-droite pour la première et droite-gauche pour la deuxième).
La logique intuitionniste est la version du calcul des séquents dont les règles sont restreintes aux séquents avec au plus une formule à droite, la contraction à droite étant considérée comme implicite.
L’idée est d’obliger une preuve à indiquer spécifiquement la conclusion dérivée, sans ambiguïté.
Et la négation est interprétée comme l’absence de preuve puisque puisque c’est maintenant seulement $\phi\vdash\bot$ qui donne $\vdash\neg\phi$. Cela rend par conséquent l’utilisation de la négation à droite impossible dans la deuxième preuve alors qu’il n’y a pas de problème dans la première.

La logique minimale est la version du calcul des séquents sans la règle de l’affaiblissement à droite et dont les règles sont restreintes aux séquents avec au plus une formule à droite (la contraction à droite n’est ici pas considérée comme implicite).
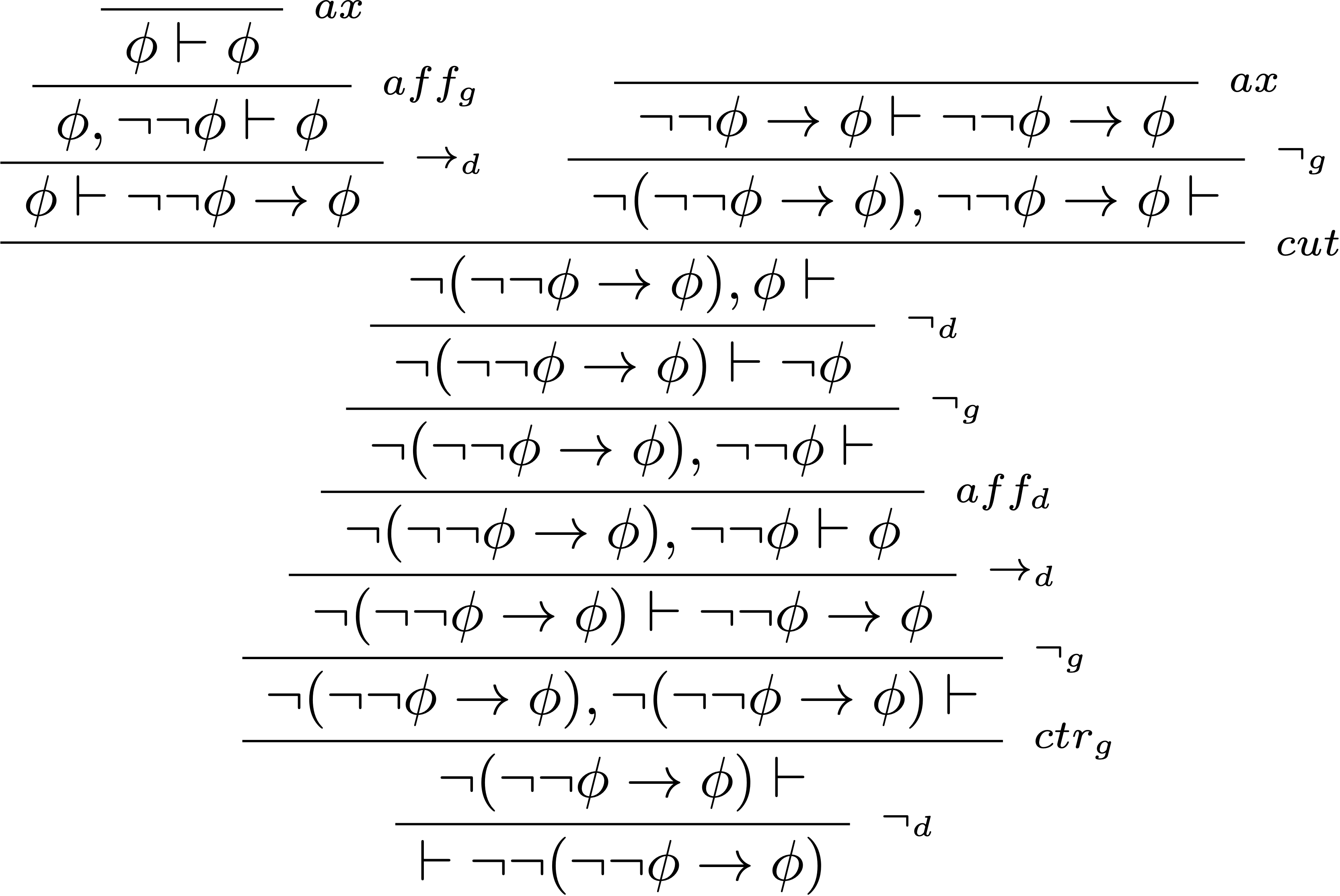
Chaque nœud de l’arbre de preuve ne contient pas plus d’une formule à droite du symbole du séquent, par contre la règle d’affaiblissement à droite est utilisée, ce qui situe cette preuve dans le cadre de la logique intuitionniste mais pas de la logique minimale.
La règle de coupure correspond, en déduction naturelle, à l’introduction de l’implication suivie aussitôt de son élimination :
Cette règle est essentielle pour tenir compte de la manière dont nous raisonnons puisqu’il arrive très souvent que l’on utilise les conclusions d’un raisonnements antérieur comme hypothèses pour de nouvelles démonstrations (hypothèses que nous faisons disparaître sur la base du fait que nous les avons démontrées).
Mais si notre objectif est d’automatiser les preuves, de les algorithmiser, les règles de coupure deviennent un handicap.
Élimination des coupures
S’il existe, en calcul des séquents classique (respectivement intuitionniste), une preuve du séquent $\Gamma\vdash\Delta$, alors il existe une preuve en calcul des séquents classique (respectivement intuitionniste) de ce séquent sans utilisation de la règle de coupure.
Tout séquent est donc prouvable par utilisation des seuls axiomes, règles logiques et règles structurelles. La démonstration du théorème consiste alors justement à remplacer dans une preuve donnée chaque utilisation de la règle de coupure par d’autres règles.
Corollaire : le séquent “$\vdash$” n’est pas prouvable en logique classique.
“$\vdash$” signifie que le vrai entraîne le faux. Nous voilà plutôt soulagé d’être dans l’incapacité de prouver ce résultat qui ferait s’effondrer tout l’édifice logique patiemment construit. Si $\vdash$ était prouvable, alors par affaiblissement, tout séquent $\vdash\Delta$ le serait également…
S’il existait une preuve du séquent $\vdash$, il en existerait aussi une sans utilisation de la règle de coupure. Or toutes les autres règles introduisent une formule soit à droite, soit à gauche, soit des deux côtés à la fois. La seule règle permettant de faire disparaître une formule est la règle de contraction, mais elle ne la fait pas disparaître complètement puisqu’elle se contente d’en faire disparaître les occurences. On ne pourra donc jamais aboutir à “$\vdash$” sans la règle de coupure et donc d’après le théorème d’élimination des coupures, on ne peut pas démontrer $\vdash$ en calcul des séquents. Youpi.
Propriété de la sous-formule
Si le séquent $\Gamma\vdash\Delta$ est prouvable en logique classique (respectivement intuitionniste), alors il existe une preuve en logique classique (respectivement intuitionniste) de ce séquent dans laquelle n’apparaîssent que des séquents constitués de sous-formules des formules de $\Gamma$ et de $\Delta$.
Il existe une preuve sans coupure de $\Gamma\vdash\Delta$. Or on peut vérifier règle par règle, par induction sur la hauteur de cette preuve sans coupure, qu’elle peut ne faire apparaître que des sous-formules de $\Gamma$ et de $\Delta$.
Une conséquence de la propriété de la sous-formule est qu’une preuve d’une disjonction en logique intuitionniste passe nécessairement par une preuve d’un des termes de la disjonction :
$\vdash_{\!i}\phi\lor\psi$ si et seulement si ($\vdash_{\!i}\phi$ ou $\vdash_{\!i}\psi$).
Par exemple, prouver une instance du tiers exclu $\Gamma\vdash_{\!i}\phi\lor\neg\phi$ en logique intuitionniste suppose qu’on a été capable soit de prouver $\Gamma\vdash_{\!i}\phi$, soit de prouver $\Gamma\vdash_{\!i}\neg\phi$, et ce n’est pas le cas en logique classique.
La conséquence majeure de la propriété de la sous-formule est de permettre (tout particulièrement en logique intuitionniste) une recherche de preuve automatique. La production mécanique de preuve comme par exemple la preuve de correction de programmes informatiques devient en effet possible une fois qu’on se débarrasse du caractère abstrait des preuves par coupures. Cela donne des preuves longues mais simples ne faisant appel qu’aux sous-formules des formules du séquent qu’il s’agit de prouver.