
Notes de lecture du livre La logique pas à pas de Jacques Duparc que je paraphrase allégrement.
Calcul des propositions
Le calcul des propositions (ou calcul propositionnel ou logique des propositions) permet de modéliser des raisonnements simples. Son pouvoir expressif est assez limité mais c’est sur ses fondations que se construisent les logiques plus évoluées.
Syntaxe
Langage
Le langage du calcul des propositions est constitué
- de variables propositionnelles $P$, $Q$, $R$,...,
- de connecteurs logiques $\neg, \lor, \land, \rightarrow, \leftrightarrow$
- et de parenthèses.
On désigna par $VAR=\Set{P,Q,R\dots}$ l’ensemble des variables propositionnelles, potentiellement infini.
- Le connectecteur logique $\neg$ est unaire (ou d'arité 1) puisqu'il transforme à lui seul une formule en une autre formule. C'est le symbole de négation et il se dit non.
- Les autres connecteurs logiques sont binaires (d'arité 2) puisqu'ils lient deux formules en une nouvelle.
- $\lor$ est le symbole de disjonction ("ou")
- $\land$ est le symbole de conjonction ("et")
- $\rightarrow$ est le symbole d'implication ("mplique")
- $\leftrightarrow$ est le symbole de double implication ou d'équivalence ("si et seulement si" ou "équivaut à")
Le langage du calcul des propositions est alors l’ensemble suivant : $\mathcal{L} = VAR\cup\Set{\neg,\lor,\land,\rightarrow,\leftrightarrow,(,)}$
Formules
On peut représenter les formules du calcul propositionnel par des arbres dont les feuilles sont des variables propositionnelles et les nœuds sont des connecteurs.
L'ensemble $\mathcal{F}$ des formules du calcul propositionnel est le plus petit ensemble d'arbres qui
- contient chaque arbre réduit à sa racine qui est une variable propositionnelle.
- chaque fois qu'il contient des formules $\phi$ et $\psi$ contient également les formules suivantes :

La hauteur d’une formule est la longueur de sa plus longue branche.
C’est une définition par récurrence (ou inductive) : on a d’abord défini les feuilles, cas de base de hauteur 0, puis on a donné la recette pour passer d’un arbre de hauteur $n$ à un arbre de hauteur $n+1$.
Une sous formule d’une formule $\phi$ est un sous-arbre de $\phi$ dont l’un des nœuds de $\phi$ est la racine.
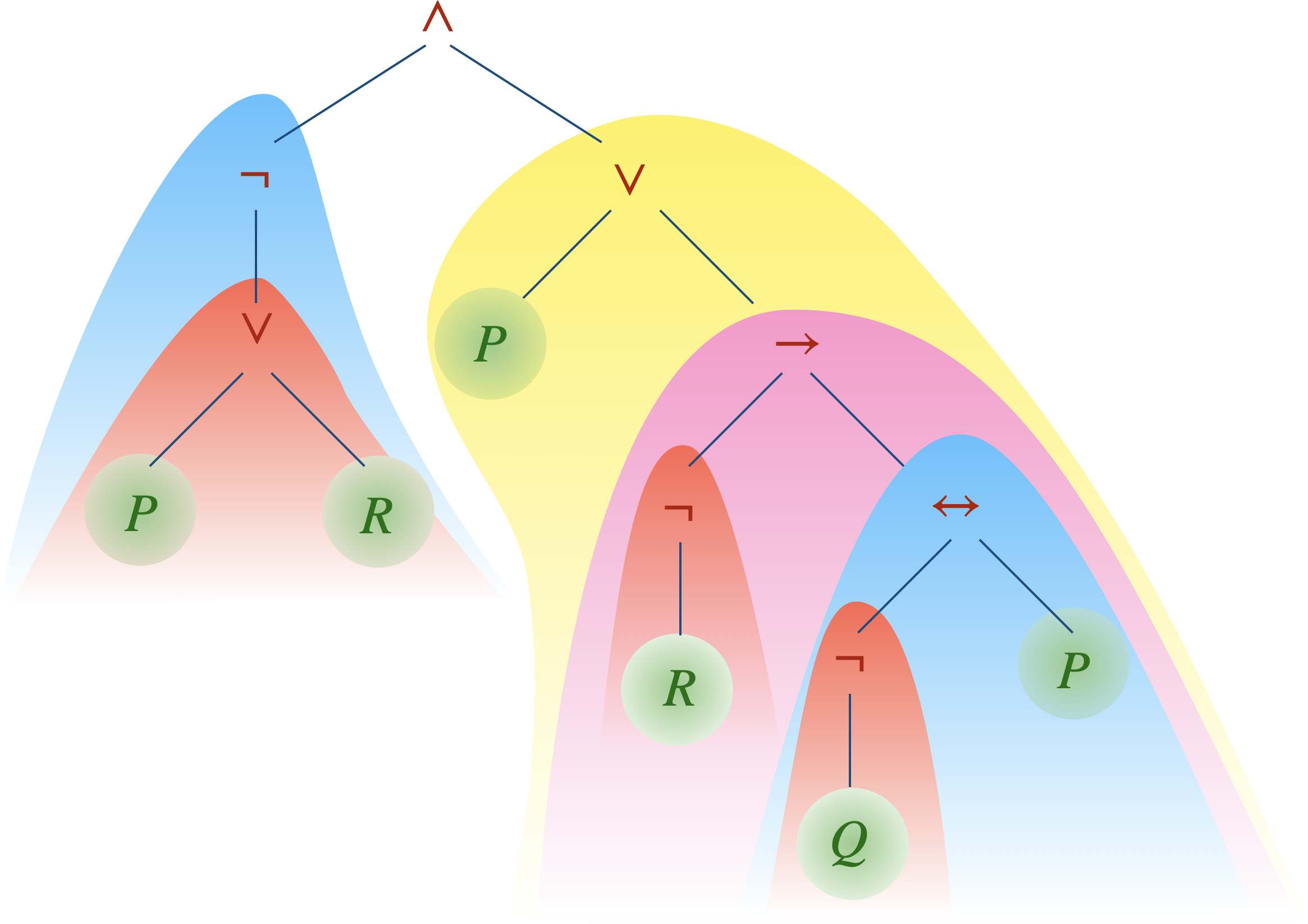
La formule de hauteur 5 ci-dessus contient :
- 5 feuilles, sous-formules de hauteur 0 (en vert),
- 3 sous-formules de hauteur 1 (en rouge),
- 2 sous-formules de hauteur 2 (en bleu),
- 1 sous-formule de hauteur 3 (en rose),
- 1 sous-formule de hauteur 4 (en jaune).
Lorsqu’une sous-formule apparaît plusieurs fois dans une formule, on dit qu’elle a plusieurs occurences.
Linéarisation d’une formule
La linéarisation d’une formule $\theta$ peut s’obtenir par induction :
- une feuille $\color{#007100}P$ se linéarise en $\color{#007100}P$ : $\theta=\color{#007100}P$
- les linéarisations des sous-formules suivantes
 sont données respectivement par $\theta=\left(\color{#B51700}{\neg}\color{#007100}{\phi}\color{#000} \right)$, $\theta=\left(\color{#007100}{\phi} \color{#B51700}{\lor} \color{#007100}{\psi} \color{#000} \right)$, $\theta=\left( \color{#007100}{\phi} \color{#B51700}{\land} \color{#007100}{\psi} \color{#000} \right)$, $\theta=\left( \color{#007100}{\phi} \color{#B51700}{\rightarrow} \color{#007100}{\psi} \color{#000} \right)$, $\theta=\left( \color{#007100}{\phi} \color{#B51700}{\leftrightarrow} \color{#007100} \psi \color{#000} \right)$.
sont données respectivement par $\theta=\left(\color{#B51700}{\neg}\color{#007100}{\phi}\color{#000} \right)$, $\theta=\left(\color{#007100}{\phi} \color{#B51700}{\lor} \color{#007100}{\psi} \color{#000} \right)$, $\theta=\left( \color{#007100}{\phi} \color{#B51700}{\land} \color{#007100}{\psi} \color{#000} \right)$, $\theta=\left( \color{#007100}{\phi} \color{#B51700}{\rightarrow} \color{#007100}{\psi} \color{#000} \right)$, $\theta=\left( \color{#007100}{\phi} \color{#B51700}{\leftrightarrow} \color{#007100} \psi \color{#000} \right)$.
Exemple :
La linéarisation de cette formule $\phi$ donne :
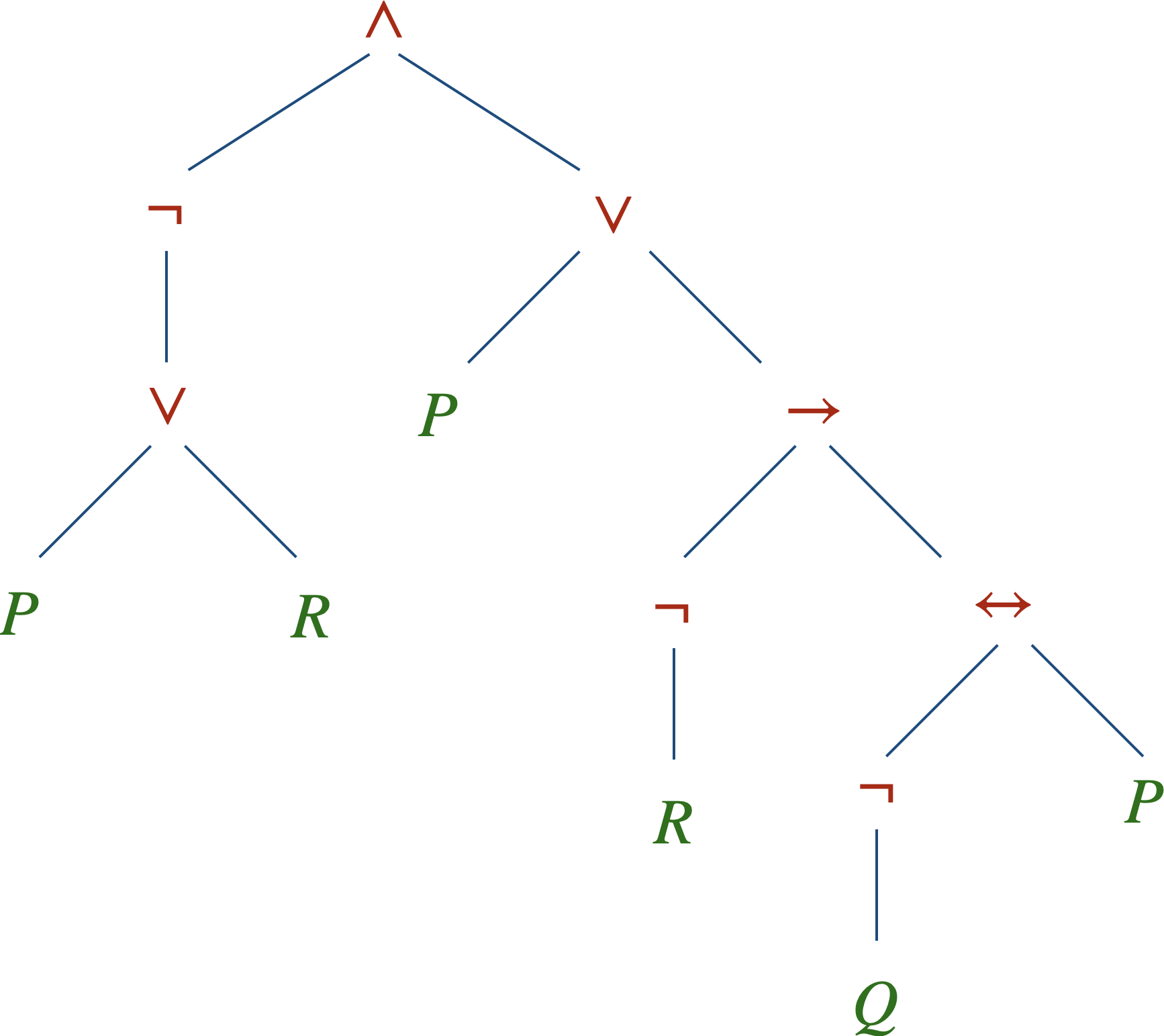
$$\displaystyle \phi = ( \color{#B51700}{\neg}\color{#000} ( \color{#007100}{P} \color{#B51700}{\lor} \color{#007100}{R}\color{#000} ) ) \color{#B51700}{\land} \color{#000} (\color{#007100}{P} \color{#B51700}{\lor}\color{#000} ( ( \color{#B51700}{\neg} \color{#007100}{R}\color{#000} ) \color{#B51700}{\rightarrow} \color{#000}( ( \color{#B51700}{\neg} \color{#007100}{Q}\color{#000} ) \color{#B51700}{\leftrightarrow} \color{#007100}{P} \color{#000} ) )) $$
La syntaxe, c’est l’articulation des symboles. La sémantique, c’est ce que ça raconte.