Algorithmique
Généralités
La notion de complexité permet de classer des algorithmes réalisant la même tâche comme dans la vidéo suivante. C’est finalement une sorte d’échelle de raffinement ; descendre d’un barreau la complexité temporelle ou spatiale demande le plus souvent de pousser la réflexion plus loin voire de repenser entièrement le problème. Et c’est ainsi qu’une recherche de doublons dans une liste se transforme en la chasse de cycles sur un graphe dans l’ultime mouture pour atteindre le Graal ($\mathcal{O}(n)$ en temps et $\mathcal{O}(1)$ en espace sans mutation).
La notion est aussi au centre d’une des plus importantes conjectures des mathématiques : $\mathrm{P}\stackrel{?}{=}\mathrm{NP}$.
Grossièrement, la conjecture revient à se demander si l’ensemble $\mathrm{NP}$ des problèmes dont les solutions sont facilement vérifiables (en temps polynomial) est le même que l’ensemble $\mathrm{P}$ des problèmes faciles (qu’on peut résoudre en temps polynomial).
Prenons l’exemple classique du voyageur de commerce.
Le problème (dans sa version décisionnelle) demande s’il existe un trajet de longueur inférieure à une valeur $K$ passant une et une seule fois par un ensemble de villes. Pour valider une solution, il suffit donc de vérifier que chaque ville est bien là une et une seule fois, calculer la distance et la comparer à $K$. Cela se fait bien sûr en temps polynomial rendant le problème $\mathrm{NP}$.
Par contre, aucun algorithme connu à ce jour ne sait aboutir à la solution en un temps mieux qu’exponentiel…
Or si $\mathrm{P=NP}$, cela voudrait dire qu’un algorithme polynomial existe bel et bien.
La grande majorité des chercheurs se rangent dans le camp pessimiste $\mathrm{P≠NP}$.
Le meilleur algorithme (non quantique) permettant de résoudre de manière exacte le problème du voyageur de commerce, l’algorithme de Held-Karp, utilise la programmation dynamique dont la logique est présentée dans la vidéo suivante.
Une implémentation de l’algorithme de Held-Karp est donnée ci-dessous. Elle utilise la technique du masquage pour parcourir tous les sous-ensembles de villes visitées possibles et pour pouvoir tester rapidement l’appartenance ou non d’une ville à ce sous-ensemble.
Code
def tsp_chemin(distance, depart=0):
"""
Résout le problème du voyageur de commerce (TSP) en utilisant une programmation dynamique basée sur les masques binaires.
Cette fonction calcule, pour chaque sous-ensemble de villes et pour chaque ville terminale, le coût minimal pour parcourir l'ensemble des villes spécifié par le masque et terminer dans cette ville.
Elle permet également de reconstruire le chemin optimal en stockant, pour chaque état, la ville précédente.
Paramètres
----------
distance : list[list[float]]
Matrice des distances entre les villes, où distance[i][j] représente la distance allant de la ville i à la ville j.
depart : int, optionnel
Indice de la ville de départ (par défaut 0).
Retourne
--------
tuple
Un tuple (dp, parent) contenant :
- dp : list[list[float]]
Tableau à deux dimensions de taille (2^n x n) où dp[masque][j] est le coût minimum pour visiter
l'ensemble de villes indiqué par le masque (représenté en binaire) et terminer à la ville j.
- parent : list[list[int]]
Tableau à deux dimensions de taille (2^n x n) permettant de reconstruire le chemin optimal.
Pour chaque état (masque, j), parent[masque][j] stocke l'indice de la ville qui précède j dans le chemin optimal.
Description
-----------
L'algorithme initialise une table dp avec des valeurs infinies, sauf pour l'état correspondant au départ.
Il parcourt ensuite tous les masques possibles (correspondant aux 2^n sous-ensembles de villes) et, pour chaque ville déjà visitée, il tente de mettre à jour le coût minimal pour atteindre chaque ville non encore visitée.
La structure parent est utilisée pour enregistrer les transitions effectuées, ce qui permet ultérieurement
de reconstruire le chemin optimal.
Exemple d'utilisation
---------------------
>>> distance = [
... [0, 10, 15, 20],
... [10, 0, 35, 25],
... [15, 35, 0, 30],
... [20, 25, 30, 0]
... ]
>>> dp, parent = tsp_chemin(distance, depart=0)
"""
n = len(distance)
INF = float('inf')
dp = [[INF] * n for _ in range(1 << n)]
parent = [[-1] * n for _ in range(1 << n)]
dp[1 << depart][depart] = 0
for masque in range(1 << n): # 2^n possibilités (chaque ville est visitée ou non visitée)
for i in range(n):
if masque & (1 << i): # si la ville i est visitée
for j in range(n):
if not (masque & (1 << j)): # si la ville j n'est pas encore visitée
nv_masque = masque | (1 << j)
if dp[nv_masque][j] > dp[masque][i] + distance[i][j]:
dp[nv_masque][j] = dp[masque][i] + distance[i][j]
parent[nv_masque][j] = i
return dp, parent
Comme à chaque fois en programmation dynamique, la matrice dp contient toutes les informations nécessaires et pour reconstruire le plus petit chemin et obtenir son coût, on peut utiliser le code suivant :
Code
def reconstr_chemin(parent, masque, dernier):
chemin = []
while dernier != -1:
chemin.append(dernier)
temp = parent[masque][dernier]
masque = masque & ~(1 << dernier)
dernier = temp
chemin.reverse()
return chemin
dp, parent = tsp(distance, depart=0)
masque_final = (1 << len(distance)) - 1
for i in range(len(distance)):
coût_total = dp[masque_final][i] + distance[i][0]
if coût_total < coût_min:
coût_min = coût_total
chemin_min = reconstr_chemin(parent, masque_final, i)
chemin_min.append(0) # Fermer le cycle
Il est basée sur la relation de récurrence suivante : $C(S,i) = \min_{j \in S,\ j \neq i} \left\{ C\left(S \setminus \{i\}, j\right) + \mathrm{d}(j,i) \right\}$ où $C(S,i)$ représente la plus petite distance pour parcourir chaque ville de l’ensemble $S$ et terminer dans la ville $i$ et $d(i,j)$ est la distance entre la ville $i$ et la ville $j$.
Sa complexité temporelle est en $\mathcal{O(n^22^n)}$. En effet, tous les sous-ensembles de villes sont inspectés $\mathcal{O}(2^n)$ et pour chacun, on parcourt toutes les paires ville de départ - ville d’arrivée possibles $\mathcal{O}(n)\times\mathcal{O}(n)$ sans jamais faire autre chose que des opérations en temps constant $\mathcal{O}(1)$ pour chaque paire.
Un algorithme de programmation dynamique ne se laisse pas approcher facilement, particulièrement dans sa forme non-récursive avec sa grosse matrice mystérieuse. Mais c’est plutôt rare que la forme itérative d’un algorithme vole la vedette à sa forme récursive tant la récursivité sait insuffler un air de magie aux algorithmes en permettant à de tout petits codes de réaliser des tâches étonnamment complexes.
Fonction centrale du programme ci-dessus :
def Hanoi(n, depart, cible, inter):
if n == 1:
deplacement(depart,cible)
else :
Hanoi(n-1,depart,inter,cible)
Hanoi(1,depart,cible,inter)
Hanoi(n-1,inter,cible,depart)
Hanoi(6, 0, 2,1)
Quelques algorithmes remarquables
Les tris sont omniprésents en informatique et Tim Roughgarden (auteur des géniaux Algorithms illuminated) en parle même comme de la “mère de tous les problèmes algorithmiques”.
Ci-dessous, vous pourrez comparer l’efficacité de différents tris par comparaison en les voyant se débattre courageusement avec les données.

Quicksort
Un code Python possible pour la version détaillée dans la vidéo :
Code
from random import randint
def partition(L, g, d):
p = L[g]
i = g+1
for j in range(g+1,d+1):
if L[j] < p:
permute(L,i,j)
i += 1
permute(L,g,i-1)
return i-1
def tri_rapide_gd(L, g, d):
if g < d:
pivot = randint(g,d)
permute(L,pivot,g)
pivot = partition(L, g, d)
tri_rapide(L, g, pivot-1)
tri_rapide(L, pivot+1, d)
return L
def tri_rapide(L):
g = 0
d = len(L)-1
tri_rapide_gd(L, g, d)
La danse hongroise ci-dessous implémente une version de l’algorithme sans hasard :
Dans cette version, le premier élément est systématiquement choisi comme pivot (chapeau noir) et la partition marche un peu différemment :
- Le chapeau rouge
iest d'abord donné au dernier élément de la partition puis comparé au pivotp. - Si le chapeau rouge est plus petit que le pivot, les deux éléments échangent leur place et le chapeau rouge est donné au plus proche voisin du côté du pivot.
- Sinon le pivot reste à sa place et le chapeau rouge est là aussi donné au voisin immédiat le plus proche du pivot.
- Lorsque le pivot récupère le chapeau rouge, il est bien placé.
- On coupe ensuite la liste en deux sur le pivot et on recommence récursivement.
Un code Python possible pour cette variante :
Code
def partition(L):
p = 0 # pivot (chapeau noir)
i = len(L)-1 # chapeau rouge
while i != p:
if (L[p]-L[i])*(p-i) < 0:
L[p],L[i] = L[i],L[p]
p,i = i,p
i -= (i-p)//abs(i-p)
return p
def tri_rapide(L):
if len(L) <= 1:
return L
else:
p = partition(L)
L[:p] = tri_rapide(L[:p])
L[p+1:] = tri_rapide(L[p+1:])
return L
Un tirage non aléatoire du pivot rend l’algorithme moins robuste sur certaines entrées. Avec le choix systématique du premier élément (par exemple), on se retrouve avec une complexité en $O(n^2)$ sur des données déjà triées ou presque. Le tirage aléatoire rend extrêmement peu probable un scénario “défavorable”.
Si en plus de choisir le premier élément comme pivot, on ne s’occupe même plus d’avoir un tri en place (c’est-à-dire qu’on s’autorise des copies de la liste de départ), Quicksort peut s’écrire de manière très compacte :
def triRapide(elements):
if len(elements) <= 1:
return elements
else:
pivot = elements[0]
plusPetit = triRapide([e for e in elements[1:] if e <= pivot])
plusGrand = triRapide([e for e in elements[1:] if e > pivot])
return plusPetit + [pivot] + plusGrand
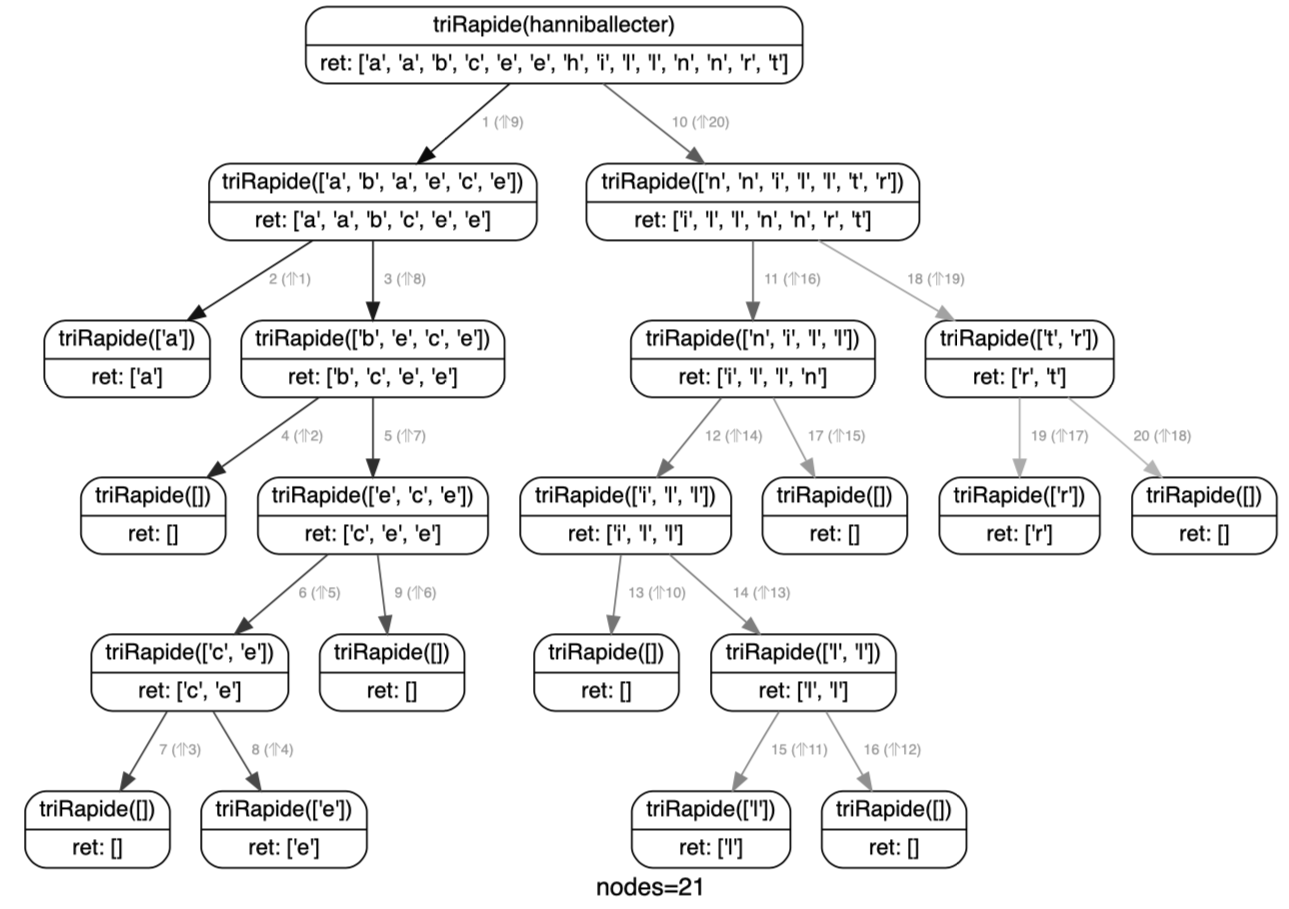
Mais attention, l’élégance de ce code cache sa lâcheté puisqu’en ne rangeant plus en place, il esquive la principale difficulté d’un algorithme de tri. S’interdire la création de nouvelles listes oblige en effet à gérer astucieusement les permutations au sein de la liste de départ. Et si cela donne souvent des codes plus verbeux, il n’en sont pas moins beaucoup plus fins.
Algorithmes gloutons
Les algorithmes gloutons sont très faciles à comprendre et à implémenter. Si on devait leur trouver un défaut, elle est à chercher du côté de leur correction, pas toujours simple à démontrer…
Sont présentés ci-dessous deux algorithmes gloutons très similaires qui permettent de résoudre des problèmes d’optimisation sur des graphes :
- Dijkstra cherche le plus court chemin entre deux nœuds.
- Prim construit l’arbre couvrant de poids minimal.
Parcours d’un graphe
Pour inventorier les sommets d’un graphe, deux stratégies sont possibles :
- le parcours en largeur (BFS),
- et le parcours en profondeur (DFS).
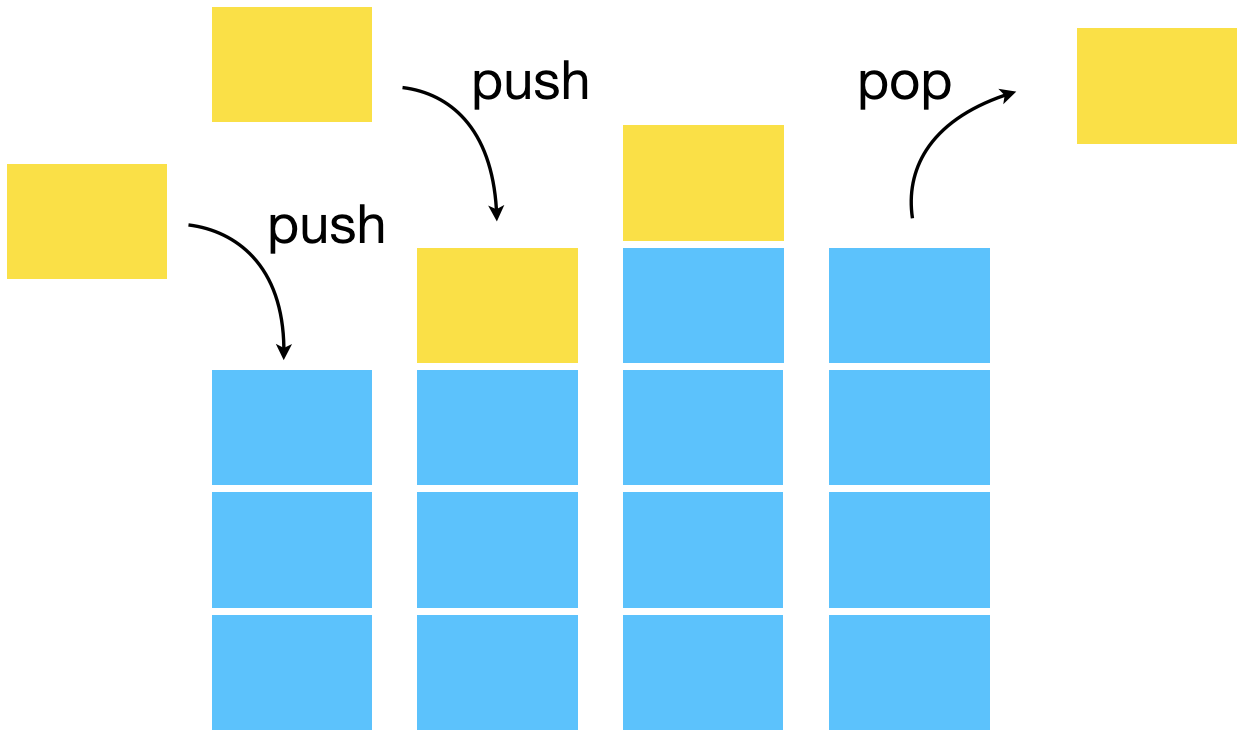
Le code est identique entre les deux algorithmes à la structure de donnée utilisée près ! On utilise une file (queue en anglais) pour le parcours en largeur et une pile pour le parcours en profondeur.
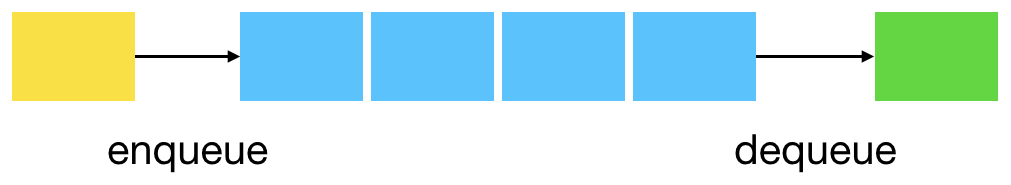
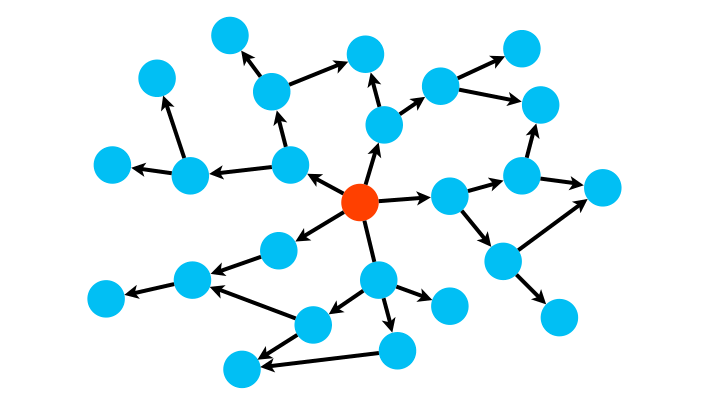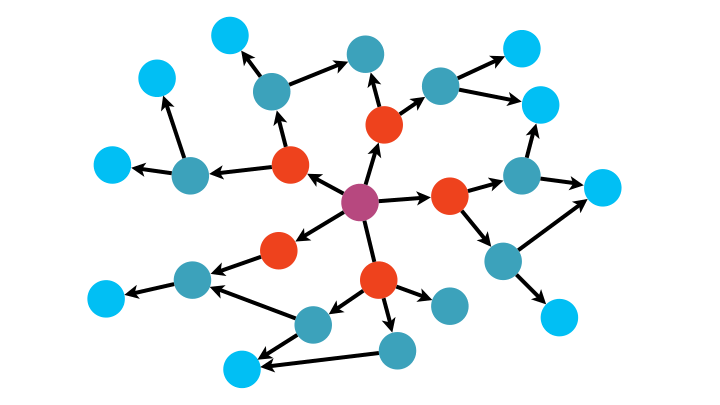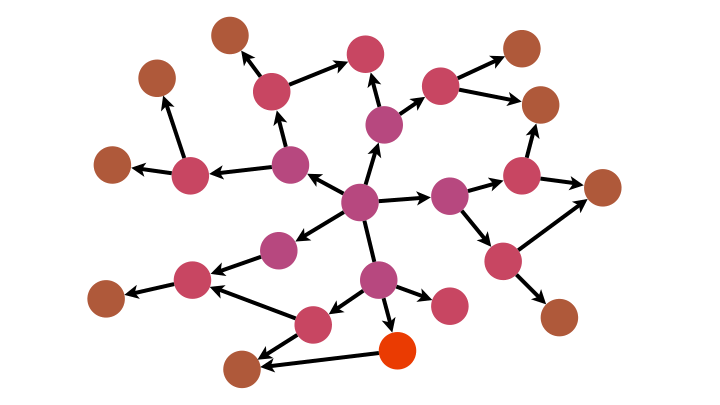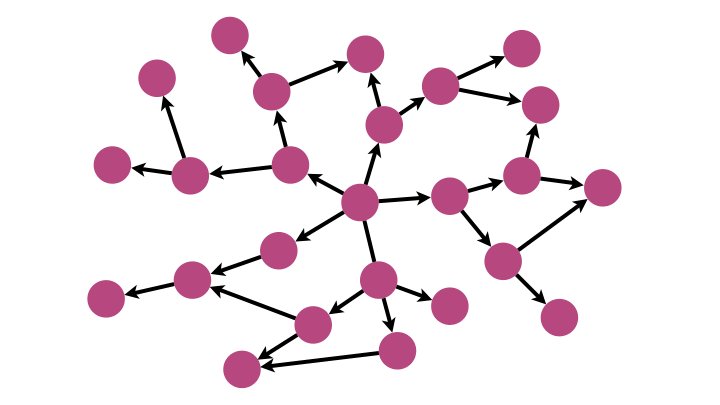
Avec sa logique FIFO (premier arrivé, premier parti, comme dans une file d’attente), BFS explore le graphe de proche en proche.
from collections import deque
# deque est une file à double extrémités (double-ended queue) avec la primitive popleft() pour retirer à gauche comme une file et pop() pour retirer à droite comme une pile.
def BFS(G,depart):
"""
graphe G(S,A) représenté par une liste d'adjacence implémentée par un dictionnaire et depart un sommet de S
"""
file = deque()
file.append(depart)
Vus = {s : False for s in G}
Sommets = []
while file: # tant que la file n'est pas vide
sommet = file.popleft() # méthode de la classe deque permettant de défiler
if not Vus[sommet]:
file += G[sommet]
Vus[sommet] = True
Sommets.append(sommet)
return Sommets
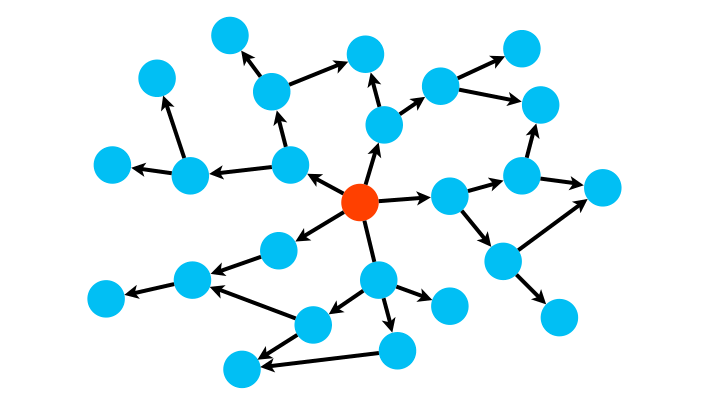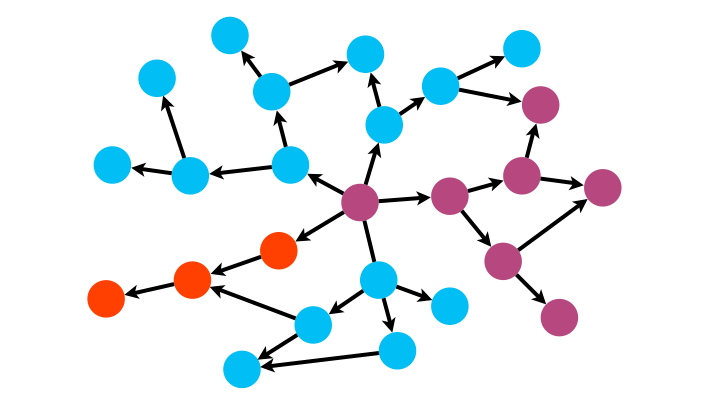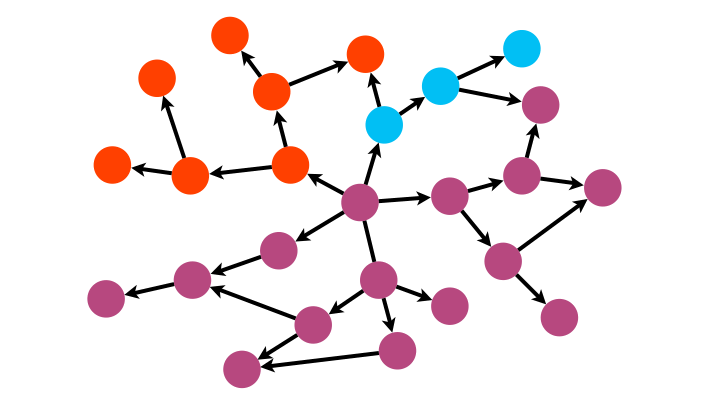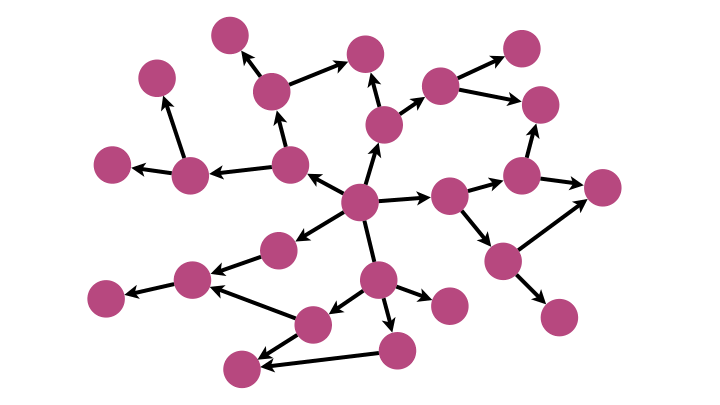
Avec sa logique LIFO (dernier, arrivée, premier parti, comme pour une pile d’assiette pendant la vaisselle), DFS s’enfonce dans une branche du graphe jusqu’à son extrémité puis revient à la dernière jonction rencontrée et explore une nouvelle branche, et ainsi de suite.
def DFS(G,depart):
pile = deque()
pile.append(depart)
Vus = {s : False for s in G}
Sommets = []
while pile:
sommet = pile.pop()
if not Vus[sommet]:
pile += G[sommet]
Vus[sommet] = True
Sommets.append(sommet)
return Sommets
Comme la récursivité utilise naturellement une pile via la pile d’exécution, il y a une écriture récursive naturelle de la recherche en profondeur.
def DFS(G,depart,Vus,Sommets=[]):
Sommets.append(depart)
Vus[depart] = True
for sommet in G[depart]:
if not Vus[sommet]:
DFS(G,sommet,Vus,Sommets)
return Sommets
On peut voir Dijkstra comme un parcours de graphe où la structure de donnée n’est plus une file ou une pile mais une file de priorité (qui donne en $\mathcal{O}(1)$ l’élément stocké de plus grand score).
Pour implémenter une file de priorité, on peut utiliser un tas (heap), arbre binaire presque ordonné dont la racine est l’élément prioritaire.
Une implémentation possible de Dijkstra :
Code
import heapq
def Dijkstra(G, depart):
"""
Calcule les plus courts chemins dans un graphe pondéré à partir d'un sommet de départ.
Paramètres :
- G : dict, représentation du graphe où les clés sont les sommets et les valeurs sont des dictionnaires {voisin: poids}.
- depart : le sommet de départ.
Retourne :
- predecesseurs : dict, permettant de reconstruire les plus courts chemins.
- distances : dict, distances minimales depuis le sommet de départ.
"""
if depart not in G:
raise ValueError("Le sommet de départ n'est pas présent dans le graphe")
distances = {sommet: float('infinity') for sommet in G}
predecesseurs = {sommet: None for sommet in G}
distances[depart] = 0
tas = [(0, depart)]
while tas:
distance_actuelle, sommet_actuel = heapq.heappop(tas)
# On ignore l'entrée obsolète si un meilleur chemin a été trouvé
if distance_actuelle > distances[sommet_actuel]:
continue
for voisin, poids in G[sommet_actuel].items():
nouvelle_distance = distance_actuelle + poids
if nouvelle_distance < distances[voisin]:
distances[voisin] = nouvelle_distance
predecesseurs[voisin] = sommet_actuel
heapq.heappush(tas, (nouvelle_distance, voisin))
return predecesseurs, distances
Algorithme d’Euclide
Une des plus vieux algorithmes ($\approx$-300).
La suite de Fibonacci est un peu la tarte à la crème du mathématicien de série télévisée avec ses spirales dans les coquillages… Mais c’est bien elle qui montre le bout de son nez là où on ne l’attendait pas vraiment dans cette vidéo sur la complexité de l’algorithme d’Euclide.
On peut utiliser le pulvérisateur (algorithme d’Euclide étendu) ci-dessous. Le code est corrigé par rapport à celui de la vidéo qui présente une erreur dans la cas de base (on doit retourner b, 0, 1 comme Euclide bien sûr et non a,0,1).
Et le petit programme qui donne la décomposition en fraction continue :
Algorithme X
Polyominos et Sudoku ont le droit à leur algorithme au nom aguicheur : X.