Théorie quantique des champs – Partie 5
Notes de lecture du livre Quantum field theory for the gifted amateur de Thomas Lancaster et Stephen Blundell. Très souvent une simple traduction.
Champs de jauge et théorie de jauge
Une invariance de jauge trahit moins une symétrie du système qu’une redondance dans sa description (différentes configurations du champ aboutissent à des observables identiques). Cette redondance nous laisse une certaine latitude quant au choix de la meilleure formulation, c’est le choix de jauge. Une transformation d’une description à une autre est appelée transformation de jauge et l’invariance sous-jacente est l’invariance de jauge.
L’invariance de jauge n’est pas une symétrie dans le sens où il n’est pas question ici de curseurs internes permettant de passer d’une particule à une autre. C’est plutôt l’affirmation de notre incapacité à trouver une description unique du système. On peut citer comme exemple l’indétermination de l’origine des potentiels électriques (le choix d’associer 0 V à la terre est arbitraire), celle de l’origine des phases en mécanique quantique (on peut passer de $\psi(x)$ à $\psi(x)\mathrm{e}^{\mathrm{i}\alpha}$ sans changer la physique), et, en électromagnétisme, la liberté sur le choix de $A$ laissé par la transformation $A \rightarrow A+\nabla \chi$ (où $\chi(\boldsymbol{x})$ est une fonction de la position) qui est sans effet sur $\boldsymbol{B}=\boldsymbol{\nabla} \times \boldsymbol{A}$. On verra que ces trois indéterminations sont en fait liées entre elles. On constate aussi que dans les trois cas, seules des variations de la grandeur indéterminée peuvent faire l’objet d’observations.
Pour avoir des définitions propres, on doit lever toute ambiguïté en fixant des jauges.
Il peut s’agir de choix de jauges globaux, identiques en tout point, ou de choix locaux, susceptibles de varier d’un point à l’autre.
Partons du Lagrangien du champ scalaire complexe :
$$ \mathcal{L}=\left(\partial^\mu \psi\right)^{\dagger}\left(\partial_\mu \psi\right)-m^2 \psi^{\dagger} \psi $$
Comme on l’a vu, la symétrie $U(1)$ se traduit par la non variation du Lagrangien (et par extension des équations du mouvement) lors de la transformation $\psi(x) \rightarrow \psi(x) \mathrm{e}^{\mathrm{i} \alpha}$. Il s’agit là d’une transformation globale puisqu’elle change le champ d’une même valeur en tout point de l’espace-temps. La théorie est donc dite invariante par transformation $U(1)$ globale.
Que se passerait-il si on imposait une invariance locale par rapport à la phase ? Il faudrait que la transformation $\psi(x) \rightarrow \psi(x) \mathrm{e}^{\mathrm{i} \alpha(x)}$ (où $\alpha(x)$ peut maintenant différer d’un point à l’autre) soit sans effet sur les équations du mouvement. Cela semble une demande un peu extrême, mais elles se révèle surprenemment féconde : l’électromagnétisme en découle !
On n’est pas embêté par le terme de masse : $m^2\psi^\dagger\psi\rightarrow m^2\psi^\dagger \mathrm{e}^{-\mathrm{i} \alpha(x)} \mathrm{e}^{\mathrm{i} \alpha(x)} \psi = m^2\psi^\dagger\psi $. Par contre, le terme contenant les dérivées pose problème puisque la dérivée agit maintenant sur $\alpha(x)$ :
$$ \begin{aligned} \partial_\mu \psi(x) & \rightarrow \partial_\mu \psi(x) \mathrm{e}^{\mathrm{i} \alpha(x)} \\ & =\mathrm{e}^{\mathrm{i} \alpha(x)} \partial_\mu \psi(x)+\psi(x) \mathrm{e}^{\mathrm{i} \alpha(x)} \mathrm{i} \partial_\mu \alpha(x) \\ & =\mathrm{e}^{\mathrm{i} \alpha(x)}\left[\partial_\mu+\mathrm{i} \partial_\mu \alpha(x)\right] \psi(x) \end{aligned} $$
Et de même, on a $\partial^\mu \psi^{\dagger}(x) \rightarrow \mathrm{e}^{-\mathrm{i} \alpha(x)}\left[\partial^\mu-\mathrm{i} \partial^\mu \alpha(x)\right] \psi^{\dagger}(x)$.
Le premier terme du Lagrangien est donc tout chamboulé :
$$ \left(\partial^\mu \psi^{\dagger}\right)\left(\partial_\mu \psi\right)-\mathrm{i}\left(\partial^\mu \alpha\right) \psi^{\dagger}\left(\partial_\mu \psi\right)+\mathrm{i}\left(\partial^\mu \psi^{\dagger}\right)\left(\partial_\mu \alpha\right) \psi+\left(\partial^\mu \alpha\right)\left(\partial_\mu \alpha\right) \psi^{\dagger} \psi $$
Faire dépendre $\alpha$ de la position a logiquement retiré sa symétrie $U(1)$ à la théorie qui n’est donc pas invariante sous une transformation $U(1)$ locale. Mais peut-on restaurer cette symétrie ?
Oui, en ajoutant un nouveau champ $A^\mu(x)$ dont la mission sera d’annuler les variations de la phase d’un point à l’autre. On greffe ce champ à la dérivée pour créer une sorte de “super dérivée” : la dérivée covariante $D_\mu$.
$$ D_\mu=\partial_\mu+\mathrm{i} q A_\mu(x) $$
La dérivée covariante peut réparer la symétrie $U(1)$ si le nouveau champ $A_\mu$ se transforme comme :
$$ A_\mu \rightarrow A_\mu-\frac{1}{q} \partial_\mu \alpha(x) $$
$q$ est le paramètre de couplage, il nous informe sur la force de l’interaction entre $A_\mu$ et les autres champs.
Si $\psi(x) \rightarrow \psi(x) \mathrm{e}^{\mathrm{i} \alpha(x)}$, alors $\partial_\mu \psi \rightarrow\left(\partial_\mu \psi\right) \mathrm{e}^{\mathrm{i} \alpha}+\mathrm{i}\left(\partial_\mu \alpha\right) \psi$ et donc
$$ \begin{aligned} D_\mu \psi=\left(\partial_\mu+\mathrm{i} q A_\mu\right) \psi & \rightarrow\left(\partial_\mu \psi\right) \mathrm{e}^{\mathrm{i} \alpha}+\mathrm{i}\left(\partial_\mu \alpha\right) \psi+\mathrm{i} q A_\mu \psi \mathrm{e}^{\mathrm{i} \alpha}-\mathrm{i}\left(\partial_\mu \alpha\right) \psi \\ & =D_\mu\left(\psi \mathrm{e}^{\mathrm{i} \alpha}\right) \end{aligned} $$
Le Lagrangien entier devient invariant si on remplace les dérivées ordinaires par des dérivées covariantes :
$$ \mathcal{L}=\left(D^\mu \psi\right)^{\dagger}\left(D_\mu \psi\right)-m^2 \psi^{\dagger} \psi $$
Pour imposer une symétrie $U(1)$ locale, la théorie se doit alors d’être invariante par rapport à deux jeux de transformations en parallèle :
$$ \begin{aligned} \psi(x) & \rightarrow \psi(x) \mathrm{e}^{\mathrm{i} \alpha(x)} \\ A_\mu(x) & \rightarrow A_\mu(x)-\frac{1}{q} \partial_\mu \alpha(x) \end{aligned} $$
Une théorie où un champ $A^\mu(x)$ est introduit pour permettre une invariance par rapport à une transformation locale est appelée théorie de jauge. Le champ $A^\mu(x)$ est appelé champ de jauge.
Le champ de jauge, introduit pour satisfaire notre envie soudaine d’invariance locale, peut-il s’avérer suffisamment réel jusqu’à avoir sa propre dynamique ?
Théorie de jauge la plus simple : l’électromagnétisme
Une théorie dont le Lagrangien contient des termes décrivant $A^\mu(x)$ se doit d’être invariante sous des transformations du type $A_\mu(x) \rightarrow A_\mu(x)-\frac{1}{q} \partial_\mu \alpha(x)$. L’électromagnétisme est justement un exemple d’une telle théorie avec son champ vectoriel $A^\mu(x)=(V(x), \boldsymbol{A}(x))$ formant le Lagrangien :
$$ \mathcal{L}=-\frac{1}{4}\left(\partial_\mu A_\nu-\partial_\nu A_\mu\right)\left(\partial^\mu A^\nu-\partial^\nu A^\mu\right)-J_{\mathrm{em}}^\mu A^\mu $$
Les équations du mouvement qu’on en déduit ne sont autres que les deux équations de Maxwell inhomogènes :
$$ \partial^2 A^\nu-\partial^\nu\left(\partial_\mu A^\mu\right)=J_{\mathrm{em}}^\nu $$
Ni le Lagrangien, ni les équations du mouvement ne sont modifiés par la transformation $A_\mu(x) \rightarrow A_\mu(x)-\partial_\mu \chi(x)$ qui se décompose en :
$$ \begin{aligned} V & \rightarrow V-\partial_0 \chi \\ \boldsymbol{A} & \rightarrow \boldsymbol{A}+\boldsymbol{\nabla} \chi \end{aligned} $$
C’est bien ce qu’on nomme en électromagnétisme l’invariance de jauge (si $A_\mu$ décrit correctement le champ électromagnétique dans une certaine situation, alors $A_\mu-\partial_\mu \chi$ aussi). Et on en déduit que l’électromagnétisme est une théorie de jauge puisqu’en choisissant de redéfinir $\chi(x)$ comme $\alpha(x)/q$, on retrouve bien la définition vue plus haut.
Comment choisir $\chi(x)$ ? Il est commun d’en passer par la jauge de Lorenz (sans “t”) :
$$ \partial_\mu A^\mu(x)=0 $$
$A_\mu$ se transforme en $A_\mu^{\prime}=A_\mu-\partial_\mu \chi$ et la jauge de Lorenz impose $\partial^\mu A_\mu^{\prime}=\partial^\mu A_\mu-\partial^\mu \partial_\mu \chi=0$. Pour la respecter, il faut donc poser $\partial^2 \chi=\partial^\mu A_\mu$.
Grâce à la jauge de Lorenz et en l’absence de courant $J_{\mathrm{em}}^\mu$, on obtient l’équation d’un champ libre sans masse. En effet l’équation du mouvement $\partial^2 A^\nu-\partial^\nu\left(\partial_\mu A^\mu\right)=J_{\mathrm{em}}^\nu$ devient $\partial^2 A^{\prime \nu}-\partial^\nu\left(\partial_\mu A^{\prime \mu}\right)=\partial^2 A^{\prime \nu}=0$ dont les solutions sont des ondes planes de la forme $A^\mu=\epsilon^\mu(p) \mathrm{e}^{-\mathrm{i} p \cdot x}$ avec $E_{\boldsymbol{p}}=|\boldsymbol{p}|$. La jauge de Lorenz fait donc ressembler l’électromagnétisme à une théorie de champ vectoriel.
On avait déjà rencontré la condition de Lorenz dans le cas du champ massif de spin 1 mais elle n’avait alors rien d’un choix ; on l’obtenait en prenant la divergence de l’équation de Proca… Mais dans tous les cas, la condition réduit le nombre de composantes indépendantes de $A’^\mu$ de quatre à trois.
Cela ne rend toujours pas $A^{\prime \mu}$ unique ici puisqu’on peut continuer à transformer le champ $A_\mu^\prime \rightarrow A_\mu^{\prime \prime}=A_\mu^{\prime}-\partial_\mu \xi$ tant que $\partial^2 \xi = 0$ ($A^{\prime \mu}$ et $A^{\prime \prime \mu}$ respectent tous deux la condition de Lorenz). Pour rendre $A^{\prime \prime \mu}$ unique, on choisit en plus de fixer $\partial_0 \xi=A_0^{\prime}$, ce qui implique $A_0^{\prime \prime}=0$.
Avec ce choix, la condition de Lorenz implique finalement la jauge de Coulomb :
$$ \boldsymbol{\nabla} \cdot \boldsymbol{A}^{\prime \prime}=0 $$
Le nombre de degrés de liberté du champ est encore réduit d’un cran.
La physique impose finalement au champ $A^\mu$ de n’avoir que deux composantes indépendantes !
Les équations du mouvement sous la jauge de Lorenz donnent $\partial^2A^\mu = 0$. Avec la condition $A^0 = 0$, cela implique des ondes planes de la forme $\boldsymbol{A}=\boldsymbol{\epsilon} \mathrm{e}^{-\mathrm{i} p \cdot x}$.
La jauge de Coulomb $\boldsymbol{\nabla} \cdot \boldsymbol{A}=0$ impose alors $\boldsymbol{p} \cdot \boldsymbol{A}=\boldsymbol{p} \cdot \boldsymbol{\epsilon}=0$ qui nous dit que la direction de propagation de l’onde est perpendiculaire à la polarisation ; l’onde est transverse !
En supposant une propagation selon l’axe $z$ avec une impulsion $q^\mu=(|\boldsymbol{q}|, 0,0,|\boldsymbol{q}|)$, on peut par exemple se donner une polarisation linéaire :
$$ \boldsymbol{\epsilon}_1(q)=\left(\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right), \quad \boldsymbol{\epsilon}_2(q)=\left(\begin{array}{l} 0 \\ 1 \\ 0 \end{array}\right) $$
ou encore une polarisation circulaire avec :
$$ \epsilon_{\mathrm{R}}^*(q)=-\frac{1}{\sqrt{2}}\left(\begin{array}{l} 1 \\ \mathrm{i} \\ 0 \end{array}\right), \quad \epsilon_{\mathrm{L}}^*(q)=\frac{1}{\sqrt{2}}\left(\begin{array}{c} 1 \\ -\mathrm{i} \\ 0 \end{array}\right) $$
Pour observer les effets du champ électromagnétique, il faut le coupler à un champ de matière. La recette la plus simple consiste à remplacer les dérivées ordinaires par les dérivées covariantes dans le Lagrangien. On nomme ce procédé couplage minimal.
Considérons un champ scalaire complexe en présence d’un champ électromagnétique. Si les champs sont indépendants, le Lagrangien total s’écrit comme la somme des Lagrangiens de chacune des théories :
$$ \mathcal{L}=\left(\partial^\mu \psi\right)^{\dagger}\left(\partial_\mu \psi\right)-m^2 \psi^{\dagger} \psi-\frac{1}{4} F_{\mu \nu} F^{\mu \nu} $$
On obtient un couplage entre les champs en passant de $\partial$ à $D$ :
$$ \begin{aligned} \mathcal{L}&= \left(D^\mu \psi\right)^{\dagger}\left(D_\mu \psi\right)-m^2 \psi^{\dagger} \psi-\frac{1}{4} F_{\mu \nu} F^{\mu \nu} \\ &= \left(\partial^\mu \psi^{\dagger}-\mathrm{i} q A^\mu \psi^{\dagger}\right)\left(\partial_\mu \psi+\mathrm{i} q A_\mu \psi\right)-m^2 \psi^{\dagger} \psi-\frac{1}{4} F_{\mu \nu} F^{\mu \nu} \\ &= \partial^\mu \psi^{\dagger} \partial_\mu \psi-m^2 \psi^{\dagger} \psi-\frac{1}{4} F_{\mu \nu} F^{\mu \nu} + {\color{#D41876}\left(-\mathrm{i} q A^\mu \psi^{\dagger}\left(\partial_\mu \psi\right)+\mathrm{i} q\left(\partial^\mu \psi^{\dagger}\right) A_\mu \psi+q^2 \psi^{\dagger} \psi A^\mu A_\mu\right) } \end{aligned} $$
Le couplage entre le champ $A^\mu$ et les champs $\psi$ et $\psi^\dagger$ est contenu dans le dernier terme et l’importance du couplage est fixée par $q$, la charge électromagnétique.
On appelle principe de jauge la notion selon laquelle un champ de jauge introduit pour assurer une symétrie locale dicte la forme du couplage, c’est-à-dire des interactions, dans la théorie.
Quantification canonique du champ électromagnétique
Le terme de masse du champ massif de spin 1 vu précédemment lui ôtait toute possibilité d’invariance de jauge alors que la nature non massive du champ de jauge lui confère cette invariance et lui retire une composante.
On obtient in fine :
$$ \hat{A}^\mu(x)=\int \frac{\mathrm{d}^3 p}{(2 \pi)^{\frac{3}{2}}} \frac{1}{\left(2 E_{\boldsymbol{p}}\right)^{\frac{1}{2}}} \sum_{\lambda=1}^2\left(\epsilon_\lambda^\mu(p) \hat{a}_{\boldsymbol{p} \lambda} \mathrm{e}^{-\mathrm{i} p \cdot x}+\epsilon_\lambda^{\mu *}(p) \hat{a}_{\boldsymbol{p} \lambda}^{\dagger} \mathrm{e}^{\mathrm{i} p \cdot x}\right) $$
avec $E_p=|\boldsymbol{p}|$.
Et l’Hamiltonien est donné par :
$$ \hat{H}=\int \mathrm{d}^3 p \sum_{\lambda=1}^2 E_{\boldsymbol{p}} \hat{a}_{\boldsymbol{p} \lambda}^{\dagger} \hat{a}_{\boldsymbol{p} \lambda} $$
Les excitations du champ électromagnétique sont des photons qu’on peut observer dans deux états de polarisation transverses.
Ces particules ont un spin $S=1$ et on en trouve deux types : $\hat{a}_{\boldsymbol{p} 1}^{\dagger}|0\rangle$ et $\hat{a}_{\boldsymbol{p} 2}^{\dagger}|0\rangle.$
Considérons un photon se propageant selon la direction $z$ avec l’impulsion $q^\mu=(|\boldsymbol{q}|, 0,0,|\boldsymbol{q}|)$. Dans une base de polarisation circulaire, on peut écrire $\epsilon_{\lambda=\mathrm{R}}^*(q)=-\frac{1}{\sqrt{2}}(0,1, \mathrm{i}, 0)$ (correspondant à $S_z = 1$) et $\epsilon_{\lambda=\mathrm{L}}^*(q)=\frac{1}{\sqrt{2}}(0,1,-\mathrm{i}, 0)$ (correspondant à $S_z = -1$). Il n’y a pas de photon avec $S^z = 0$ puisque cela correspondrait à une polarisation longitudinale interdite $\epsilon_{\lambda=3}^*(p)=(0,0,0,1).$
Symétries discrètes
On a rencontré jusque-là des symétries portées par des transformations continues (translations, rotations) représentées par des groupes continus (groupes de Lie). Mais on peut aussi rencontrer des symétries correspondant à des transformations discrètes représentées cette fois-ci par des groupes finis.
Conjugaison de charge
On appelle conjugaison de charge la transformation qui change une particule en son antiparticule. C’est l’opérateur $\text { C }$ qui se charge de cette prouesse. Il ne permute pas seulement la charge d’une particule, mais aussi son nombre leptonique, son hypercharge et tout autre “nombre de charge”. On a alors :
$$ \mathrm{C}|p\rangle=|\bar{p}\rangle $$
La charge d’une particule $p$ de charge $q$ est mesurée par un opérateur $\hat{Q}$ : $\hat{Q}|p\rangle=q|p\rangle$. Par contre : $\hat{Q}|\bar{p}\rangle=-q|\bar{p}\rangle$. On peut donc écrire $\mathrm{C} \hat{Q}|p\rangle=q \mathrm{C}|p\rangle=q|\bar{p}\rangle$, mais $\hat{Q} \mathrm{C}|p\rangle=\hat{Q}|\bar{p}\rangle=-q|\bar{p}\rangle$, ce qui implique que $\hat{Q} \mathrm{C}=-\mathrm{C} \hat{Q}$, ou de manière équivalente :
$$ \mathrm{C}^{-1} \hat{Q} \mathrm{C}=-\hat{Q} $$
L’échange entre particule et antiparticule impose :
$$ \mathrm{C}^{-1} \hat{a}_{\boldsymbol{p}} \mathrm{C}=\hat{b}_{\boldsymbol{p}} \quad\quad \mathrm{C}^{-1} \hat{b}_{\boldsymbol{p}}^{\dagger} \mathrm{C}=\hat{a}_{\boldsymbol{p}}^{\dagger} $$
Et comme un champ scalaire $\hat{\psi}(x)$ peut s’écrire $\hat{\psi}(x)=\int_{\boldsymbol{p}}\left(\hat{a}_{\boldsymbol{p}} \mathrm{e}^{-\mathrm{i} p \cdot x}+\hat{b}_{\boldsymbol{p}}^{\dagger} \mathrm{e}^{\mathrm{i} p \cdot x}\right)$, on doit avoir $\mathrm{C}^{-1} \hat{\psi} \mathrm{C}=\hat{\psi}^{\dagger}$ ($\hat{\psi}^{\dagger}=\int_{\boldsymbol{p}}\left(\hat{a}_{\boldsymbol{p}}^{\dagger} \mathrm{e}^{\mathrm{i} p \cdot x}+\hat{b}_{\boldsymbol{p}} \mathrm{e}^{-\mathrm{i} p \cdot x}\right)$).
Comme $\mathrm{C}^2=I$, les valeurs propre de $\mathrm{C}$ ne peuvent être que $\pm 1$. La plupart des particules ne sont pas des états propres de $\mathrm{C}$ puisque si elles l’étaient, on aurait $\mathrm{C}|p\rangle=|\bar{p}\rangle= \pm|p\rangle$, ce qui impliquerait que $|\bar{p}\rangle$ est le même état que $|p\rangle$ et donc que la particule est sa propre antiparticule. C’est vrai pour les particules sans charge quantique.
Le photon $\gamma$, lui, est un état propre de $\mathrm{C}$ avec la valeur propre $-1$, puisqu’en changeant totues les particules en leurs antiparticules, le champ électromagnétique est renversé ($A^\mu \rightarrow-A^\mu$). C’est aussi le cas pour le pion neutre $\pi^0$, mais avec la valeur propre $+1$. Cela explique pourquoi la réaction $\pi^0 \rightarrow \gamma+\gamma$ est autorisée alors que $\pi^0 \rightarrow \gamma+\gamma+\gamma$ est impossible.
Parité
Une symétrie miroir inverse la direction de l’axe perpendiculaire au miroir et conserve les autres. Si on fait suivre cette transformation d’une rotation à 180° autour de l’axe perpendiculaire au miroir, on aura inversé toutes les directions spatiales, opérant ainsi une inversion spatiale ($\boldsymbol{x}\rightarrow-\boldsymbol{x}$). Cette transformation, appelée parité, est prise en charge par l’opérateur $\mathrm{P}$. L’opérateur position va donc anticommuter avec l’opérateur parité :
$$ \hat{\boldsymbol{x}} \mathrm{P}=-\mathrm{P} \hat{\boldsymbol{x}} $$
Ou de manière équivalente :
$$ \mathrm{P}^{-1} \hat{\boldsymbol{x}} \mathrm{P}=-\hat{\boldsymbol{x}} $$
L’effet sur les coordonnées de l’impulsion est le même ($p \rightarrow-\boldsymbol{p}$) et donc :
$$ \mathrm{P}^{-1} \hat{\boldsymbol{p}} \mathrm{P}=-\hat{\boldsymbol{p}} $$
L’opérateur $\mathrm{P}$ est hermitien et son propre inverse ($\mathrm{P}^2=I$), donc $\mathrm{P}$ est aussi un opérateur unitaire.
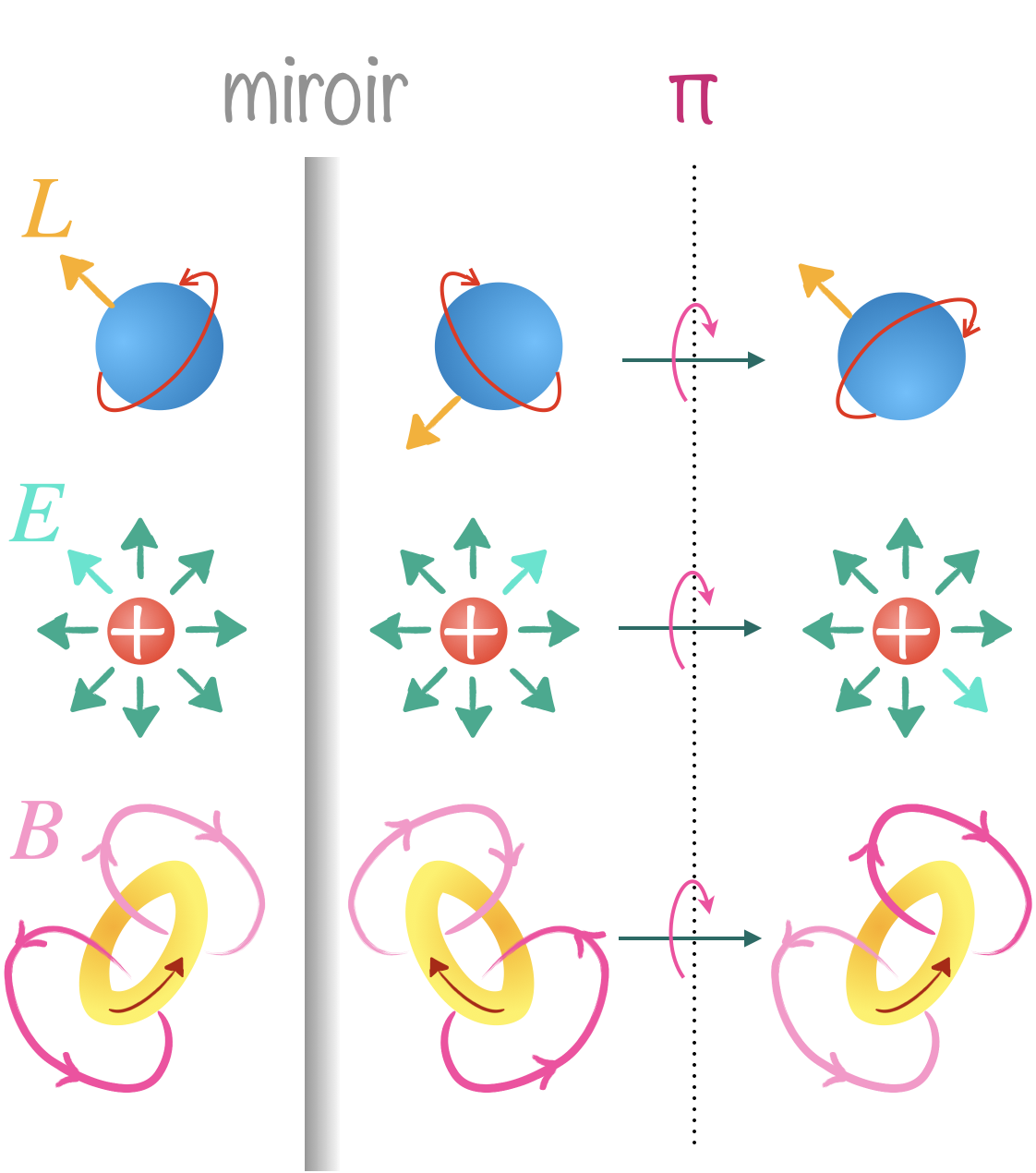
L’opérateur de parité est sans effet sur les scalaires mais renverse les vecteurs. Mais il existe une classe spéciale de scalaire et de vecteurs (même si pas réellement des scalaires et des vecteurs mais plutôt des ojets composites) pour lesquels ce n’est pas vrai : les pseudoscalaires formés par un produit mixte et les pseudovecteurs (aussi appelés vecteurs axiaux) formés par un produit vectoriel entre vecteurs ordinaires (aussi appelés vecteurs polaires).
Le champ électrique $\boldsymbol{E}$ agit comme un vecteur ordianaire (polaire) alors que le champ magnitique et le moment cinétique $\boldsymbol{L}$ sont des pesudovecteurs (vecteurs axiaux).
$$ \begin{aligned} \mathrm{P}(\text { scalaire })&=\text { scalaire }\\ \mathrm{P}(\text { pseudoscalaire })&=-\text { pseudoscalaire }\\ \mathrm{P}(\textbf{ vecteur })&=- \text {\bf vecteur }\\ \mathrm{P}(\textbf{ pseudovecteur })&= \text {\bf pseudovecteur } \end{aligned} $$
Comme $\mathrm{P}^2 = I$, sous la multiplication, le groupe ${I, P}$ est isomorphe à $\mathbb{Z}_2$, le groupe cyclique d’ordre 2.
$$ \begin{array}{c|cc} & I & \mathrm{P} \\ \hline I & I & \mathrm{P} \\ \mathrm{P} & \mathrm{P} & I \end{array} $$
Comme pour $\mathrm{C}$, cela signifie que les valeurs propres de $\mathrm{P}$ sont $\pm1$. Les scalaires et pseudovecteurs ont une valeur de parité de $+1$ alors que pseudoscalaires et vecteurs ont une parité de $-1$.
Le photon étant une excitation d’un champ vectoriel non massique, il possède une parité intrinsèque de $-1$. Le pion est, lui, décrit par un champ pseudoscalaire et a donc aussi une parité de $-1$. On verra plus tard que la parité d’un fermion est opposée à celle de son antiparticule.
La complication avec l’opérateur de parité est qu’il agit à la fois sur les coordonnées du champ et sur la nature même du champ.
Prenons le cas d’un champ scalaire. La parité va faire en sorte que $\phi(t, \boldsymbol{x}) \rightarrow \phi(t,-\boldsymbol{x})$. Étudions maintenant son action sur les opérateurs de création et d’annihilation :
$$ \mathrm{P}^{-1} \hat{\phi}(t, \boldsymbol{x}) \mathrm{P}=\hat{\phi}(t,-\boldsymbol{x})=\int_{\boldsymbol{p}} \hat{a}_{\boldsymbol{p}} \mathrm{e}^{-\mathrm{i}(E t+\boldsymbol{p} \cdot \boldsymbol{x})}+\hat{a}_{\boldsymbol{p}}^{\dagger} \mathrm{e}^{\mathrm{i}(E t+\boldsymbol{p} \cdot \boldsymbol{x})} $$
C’est possible si $\mathrm{P}^{-1} \hat{a}_{\boldsymbol{p}} \mathrm{P}=\hat{a}_{-{\boldsymbol{p}}}$ et $\mathrm{P}^{-1} \hat{a}_{\boldsymbol{p}}^{\dagger} \mathrm{P}=\hat{a}_{-\boldsymbol{p}}^{\dagger}$. L’opérateur de parité renverse simplement les impulsions pour les opérateurs de création et d’annihilation.
Renversement du temps
L’opérateur renversement du temps $\mathrm{T}$ transforme un champ scalaire $\phi(t, \boldsymbol{x})$ en $\phi(-t, \boldsymbol{x})$. Elle laisse donc le vecteur position tranquille :
$$ \mathrm{T}^{-1} \hat{\boldsymbol{x}} \mathrm{~T}=\hat{\boldsymbol{x}} $$
Mais elle renverse l’impulsion :
$$ \mathrm{T}^{-1} \hat{\boldsymbol{p}} \mathrm{~T}=-\hat{\boldsymbol{p}} $$
La seule possibilité pour préserver la relation de commutation $\left[\hat{x}, \hat{p}_x\right]=\mathrm{i}$ est que $\mathrm{T}$ soit antiunitaire puisqu’il faut que $\mathrm{T}^{-1} \mathrm{i} \mathrm{~T}=-\mathrm{i}$.
Pour un opérateur antiunitaire, $\mathrm{T}^2=-I$. On peut noter aussi que $\mathrm{T}^{-1} \mathrm{i} \mathrm{~T}=-\mathrm{i}$ équivaut à $\mathrm{i} T=-\mathrm{Ti}$ ce qui signifie que $\mathrm{i}$ anticommute avec $\mathrm{T}$.
L’opérateur antiunitaire archétypal est $\mathrm{K}$, l’opérateur de conjugaison complexe. Et on peut construire un opérateur antiunitaire général par le produit d’un opérateur unitaire $\mathrm{U}$ et de $\mathrm{K}$. Écrivons ainsi $\mathrm{T}=\mathrm{UK}$, qui équivaut (en multipliant les deux membres à droite par $\mathrm{K}$) à $\mathrm{U}=\mathrm{T} \mathrm{K}$.
Pour des particules sans spin, on peut choisir $\mathrm{U}=I$ et $\mathrm{U}=\mathrm{K}$. Ce n’est pas surprenant si on regarde l’effet de la conjugaison complexe sur l’équation de Schrödinger :
$$ \begin{gathered} \hat{H} \psi=\mathrm{i} \frac{\partial \psi}{\partial t} \\ \hat{H} \psi^*=-\mathrm{i} \frac{\partial \psi^*}{\partial t}=\mathrm{i} \frac{\partial \psi^*}{\partial(-t)} \end{gathered} $$
La combinaison d’un renversement du temps et d’une conjugaison complexe laisse invariante l’équation de Schrödinger. Ça semble bien montrer que dans ce cas, $\mathrm{K}$ et $\mathrm{T}$ sont une seule et même transformation.
Pour des particules avec spin, les choses se compliquent puisque le moment cinétique est renversé lorsqu’on change le sens d’écoulement du temps. Et donc l’action de $\mathrm{T}$ sur l’opérateur de spin $\hat{\boldsymbol{S}}$ s’écrit :
$$ \mathrm{T}^{-1} \hat{\boldsymbol{S}} \mathrm{~T}=-\hat{\boldsymbol{S}} $$
En se rappelant que seul la matrice de Pauli $\sigma_y$ a des composantes complexes, l’action de l’opérateur de conjugaison complexe sur les opérateurs de spin est plus tordue :
$$ \mathrm{K}^{-1} \hat{S}_x \mathrm{~K}=\hat{S}_x, \quad \mathrm{~K}^{-1} \hat{S}_y \mathrm{~K}=-\hat{S}_y, \quad \mathrm{~K}^{-1} \hat{S}_z \mathrm{~K}=\hat{S}_z $$
Une forme appropriée pour $\mathrm{U}$ serait donc $\mathrm{U}=\exp \left(-\mathrm{i} \pi \hat{S}_y\right)$ correspondant à une rotation de π autour de la direction $y$ de telle sorte qu’en combinant $\mathrm{U}$ et $\mathrm{K}$, on renverse bien les trois composantes du spin. On a ainsi :
$$ \mathrm{T}=\exp \left(-\mathrm{i} \pi \hat{S}_y\right) \mathrm{K} $$
On obtient alors :
$$ \mathrm{T}^2=\mathrm{U}\mathrm{K}\mathrm{U}\mathrm{K}=\exp \left(- \mathrm{i} \pi \hat{S}_y\right)\exp \left(+\mathrm{i} \pi (-\hat{S}_y)\right)=\exp \left(- 2\mathrm{i} \pi \hat{S}_y\right)=(-1)^{2S} $$
Pour un électron unique, on a $S=\frac{1}{2}$ et donc $\mathrm{T}^2=-1$. Cela reste le cas si on a un nombre impair d’électrons, mais si le nombre est pair, alors $\mathrm{T}^2=1$.
Plaçons-nous dans le cas où le nombre d’électrons est impair et supposons que l’Hamiltonien $\mathcal{H}$ du système est invariant par rapport à une inversion temporelle ($\mathcal{H}$ commute avec $\mathrm{T}$). Les états $|\psi\rangle$ et $\mathrm{T}|\psi\rangle$ ont alors la même énergie. Mais correspondent-ils au même état ? S’ils l’étaient, on aurait $\mathrm{T}|\psi\rangle=\alpha|\psi\rangle$ où $\alpha$ est un nombre complexe. Mais alors, $\mathrm{T}^2|\psi\rangle=\mathrm{T} \alpha|\psi\rangle=\alpha^* \mathrm{~T}|\psi\rangle=|\alpha|^2|\psi\rangle$ et comme $\mathrm{T}^2=-1$, on aboutit à une contradiction $|\alpha|^2=-1$. Conclusion, $|\psi\rangle$ et $\mathrm{T}|\psi\rangle$ sont linéairement indépendants et sont appelés doublets de Kramers. On vient ainsi de déduire que les niveaux d’énergie d’un système temporellement symétrique avec un nombre impair d’électrons sont $n$-fois dégénérés avec un $n$ pair. C’est le théorème de Kramers. Pour séparer ces paires, il faut introduire une perturbation qui brise la symétrie temporelle, comme un champ magnétique.
Combinaisons de transformations discrètes
En renversant à la fois le temps $t$ avec $\mathrm{T}$ et les coordonnées spatiales $\boldsymbol{x}$ avec $\mathrm{P}$, on obtient un renversement complet de l’espace-temps $x$. Sur un champ scalaire, on obtient :
$$ (\mathrm{PT})^{-1} \hat{\phi}(x)(\mathrm{PT})=\hat{\phi}(-x) $$
Cette opération laisse les opérateurs de création et d’annihilation inchangés puisque l’impulsion est retournée une fois par l’opération de parité et une nouvelle fois par le renversement du temps.
$$ (\mathrm{PT})^{-1} \hat{a}_{\boldsymbol{p}}(\mathrm{PT})=\hat{a}_{\boldsymbol{p}} \quad(\mathrm{PT})^{-1} \hat{a}_{\boldsymbol{p}}^{\dagger}(\mathrm{PT})=\hat{a}_{\boldsymbol{p}}^{\dagger} $$
Le seul effet sur la décomposition en modes est alors de changer le signe de $\mathrm{i}$ dans l’exponentielle. $\mathrm{P}\mathrm{T}$ agit donc comme un opérateur de conjugaison complexe.
Les symétries liées à $\mathrm{C}$, $\mathrm{P}$ et $\mathrm{T}$ sont chacune conservées dans la plupart des processus à plusieurs particules, mais pas tous. $\mathrm{P}$ est par exemple “violée” en interaction faible.
Théorème $\mathrm{CPT}$ :
Si le Lagrangien d’une théorie est invariant de Lorentz, local, hermitien et normalement ordonné, alors la théorie possède la symétrie $\textrm{CPT}$ ; renverser à la fois l’espace-temps et les particules en antiparticules doit laisser la théorie invariante.
La preuve consiste à montrer que $(\mathrm{CPT})^{-1} \mathcal{L}(x)(\mathrm{CPT})=\mathcal{L}(-x)$ et ainsi d’en déduire que $\mathrm{CPT}$ commute avec l’Hamiltonien et est donc une symétrie. Jusqu’ici, la symétrie $\mathrm{CPT}$ a résisté à tous les tests.
Combinaisons de transformations discrètes et continues
$SO(3)$, le groupe orthogonal spécial, est le groupe des rotations à 3 dimensions représentées par des matrices $3\times 3$ orthogonales et de déterminant $+1$ (spéciales). Ces rotations qui respectent l’orientation (c’est ce qu’assure le déterminant de $+1$) sont dites propres.
La transformation de parité peut être représentée par la matrice $\text{diag}(-1,-1,-1)$ :
$$ \left(\begin{array}{ccc} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{array}\right) $$
Là, le déterminant est clairement $-1$. En combinant avec $SO(3)$, c’est-à-dire en s’autorisant les rotations impropres (ne conservant pas l’orientation), on obtient le groupe $O(3)$ de toutes les matrices orthogonales $3\times 3$.
L’othogonalité implique $R^TR = I$ et en prenant le déterminant $\operatorname{det} \mathbf{R} \times \operatorname{det} \mathbf{R}^{\mathrm{T}}=1$. Et comme $\operatorname{det} \mathbf{R}=\operatorname{det} \mathbf{R}^{\mathrm{T}}$, on obtient $(\operatorname{det} \mathbf{R})^2=1$. D’où les deux possibilités $\operatorname{det} \mathbf{R}= \pm 1$.
Le groupe $O(3)$ est composé de deux ensembles disjoints liés l’un à l’autre par une parité. Seul l’ensemble spécial correspond à un groupe indépendant car lui seul possède l’identité.
Pour obtenir $\text{diag}(-1,-1,-1)$, l’opération de parité, on peut faire le produit d’une réflexion par un miroir dans le plan $x-y$, représentée par $\text{diag}(1,1,-1)$ par une rotation de $\pi$ autour de l’axe $z$, représentée par $\text{diag}(-1,-1,1)$. En tant que produit entre une rotation impropre et une rotation propre, l’opération de parité est une rotation impropre.
$SO(3)$ est un groupe connexe dans le sens où on peut se promener continument d’un élément à l’autre. Au contraire, $O(3)$ consiste en l’union de deux ensembles disjoints ; celui des éléments de déterminant $+1$ et celui des déterminants $-1$.
On obtient quelque chose de similaire avec le groupe de Lorentz (souvent appelé $O(3,1)$, pour distinguer les 3 directions spatiales de la direction temporelle) contenant toutes les rotations, réflexions et boosts de Lorentz. Ce groupe consiste en 4 composants séparés topologiquement car en plus de $\mathrm{P}$, on doit considérer $\mathrm{T}$.
Dans une représentation à 4 dimensions, $\mathrm{P}=\operatorname{diag}(1,-1,-1,-1)$ et $\mathrm{T}=\operatorname{diag}(-1,1,1,1)$. Le sous-groupe du groupe de Lorentz qui ne renverse ni les coordonnées spatiales ni temporelles est appelé sous-groupe propre (conserve l’orientation spatiale) orthochrone (conserve l’orientation du temps) de Lorentz $SO^+(1,3)$. Ce sous-groupe connexe est une des quatre composantes du groupe de Lorentz. On accède aux autres composantes à partir de $SO^+(1,3)$ :
- par action de $\mathrm{P}$,
- par action de $\mathrm{T}$,
- par action de $\mathrm{PT}$.
Revenons enfin sur $SO(3)$ et sa topologie. Une rotation est caractérisée par un axe et un angle. Par conséquent, tous les points dans une boule de rayon $\pi$ peuvent représenter une rotation (l’axe est donné par le vecteur entre le centre de la sphère et le point choisi et l’angle est donné par la norme de ce vecteur). Dans cette représentation, deux points antipodaux correspondent à le même rotation (une rotation de $\pi$ autour d’un axe est équivalente à une rotation de $-\pi$ autour de l’axe inverse). La topologie de $SO(3)$ est donc celle d’une boule dont les points antipodaux de la surface sont identifiés entre eux (on peut se téléporter d’un point à l’autre).
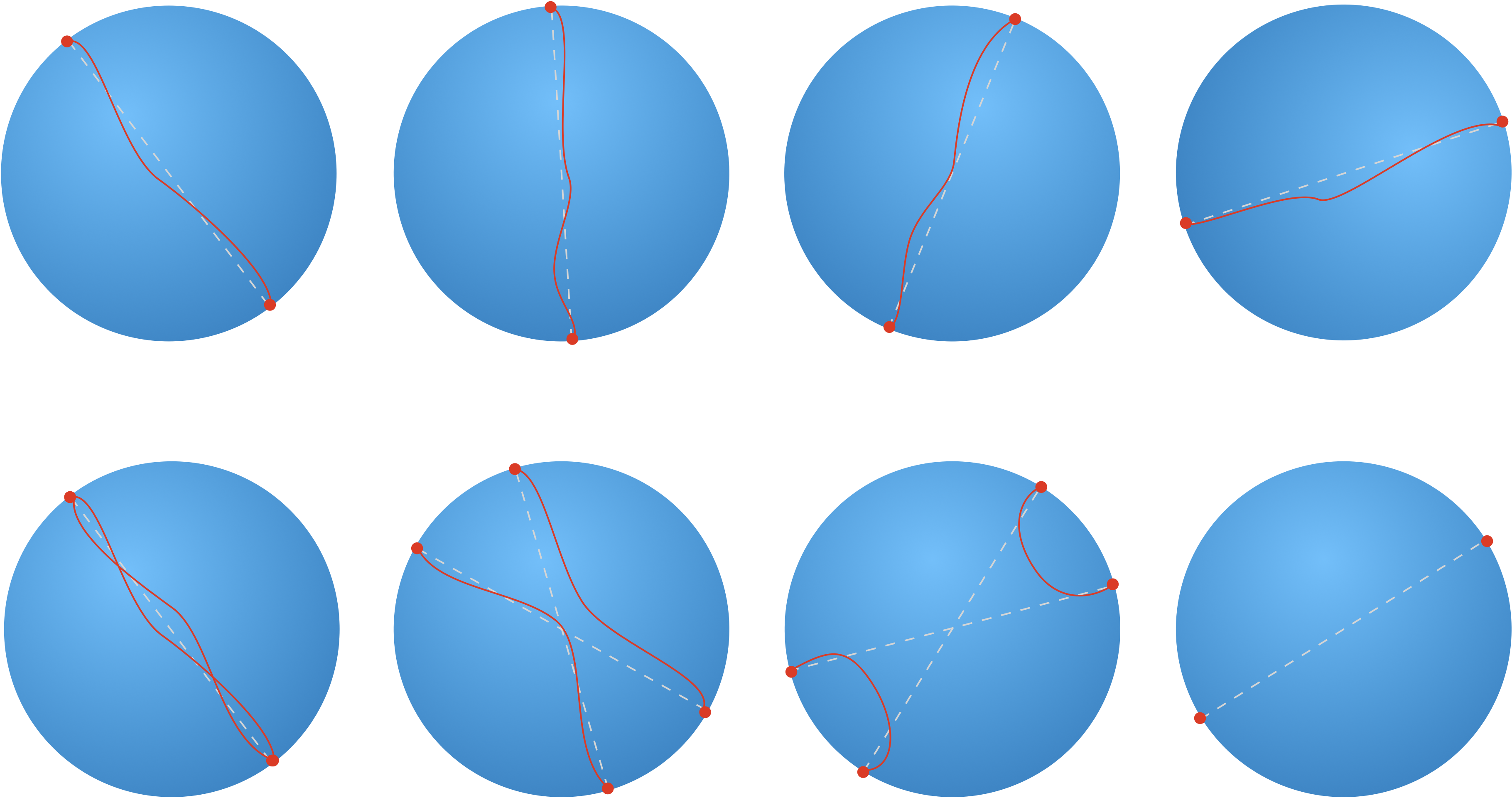
Cela signifie que l’espace topologique de $SO(3)$ est connexe mais pas simplement connexe. En effet, dans un espace simplement connexe, tout lacet (chemin continu fermé) doit pouvoir se réduire continument à un point. Or ici, le lacet allant d’un pôle à l’autre (ce chemin est bien un lacet puisque ses extrémités correspondent à un seul et même point) n’est pas déformable en un point puisque tout mouvement d’une extrémité s’accompagne d’un mouvement opposé de l’autre extrémité pour rester antipodal. Par contre, en faisant un deuxième tour d’un pôle à l’autre, on peut maintenant faire disparaître le lacet comme le montre le dessin ci-dessus. Cela montre que les rotations de $4\pi$ sont continument déformables en un point alors que les rotations de $2\pi$ ne le sont pas. La “ceinture de Dirac” ou les “assiettes de Feynman” tentent d’illustrer expérimentalement ce phénomène.
On peut faire correspondre les rotations 3D aux éléments d’un autre groupe : $SU(2)$, le groupe spécial unitaire représenté par des matrices $2\times 2$ de déterminant 1. Les éléments de $SU(2)$ permettent de faire tourner les spineurs.
Une matrice de rotation peut en effet s’écrire $\mathbf{R}(\hat{\boldsymbol{n}}, \theta)$ avec :
$$ \mathbf{R}(\hat{\boldsymbol{n}}, \theta)=\exp \left(-\mathrm{i} \frac{\theta}{2} \boldsymbol{\sigma} \cdot \boldsymbol{n}\right)=I \cos \frac{\theta}{2}-\mathrm{i} \sin \frac{\theta}{2} \boldsymbol{\sigma} \cdot \boldsymbol{n} $$
où $\boldsymbol{\sigma}=\left(\sigma_x, \sigma_y, \sigma_z\right)$ sont les matrices de Pauli et $I$ la matrice identité. On remarque alors que :
$$ \mathbf{R}(\hat{\boldsymbol{n}}, 0)=I\quad,\quad \mathbf{R}(\hat{\boldsymbol{n}}, 2 \pi)=-I \quad,\quad \mathbf{R}(\hat{\boldsymbol{n}}, 4 \pi)=I $$
On dit que $SU(2)$ est un double recouvrement de $SO(3)$. Prenons l’identité par exemple : dans $SO(3)$, l’absence de rotation est représentée par $\operatorname{diag}(1,1,1)$ et dans $SU(2)$, à la fois par $\operatorname{diag}(1,1)$ et $\operatorname{diag}(-1,-1)$.
Un spineur peut s’écrire comme une entité à deux composantes $\binom{a}{b}$ où $a$ et $b$ sont des nombres complexes tels que $|a|^2+|b|^2=1$. En écrivant $a=x_0+\mathrm{i} x_1$ et $b=x_2+\mathrm{i} x_3$ où les $x_i$ sont des nombres réels, la condition $|a|^2+|b|^2=1$ devient $x_0^2+x_1^2+x_2^2+x_3^2=1$ et donc $SU(2)$ est isomorphe à $S^3$, la 3-sphère, ce qui montre que $SU(2)$ est simplement connexe, contrairement à $SO(3)$. $SO(3)$ est finalement un groupe quotient : $S O(3) \cong S U(2) / \mathbb{Z}_2$.
On peut généraliser ces arguments à la composante connexe du groupe de Lorentz : $S O(1,3) \cong S L(2, \mathbb{C}) / \mathbb{Z}_2$ où $S L(2, \mathbb{C})$ est le groupe des matrices $2\times 2$ complexes de déterminant unité.