Théorie quantique des champs – Partie 3
Notes de lecture du livre Quantum field theory for the gifted amateur de Thomas Lancaster et Stephen Blundell. Très souvent une simple traduction.
Évolution temporelle
Deux représentations de la mécanique quantique s’opposent quant à la description de l’évolution temporelle d’un système : la représentation de Schrödinger et la représentation d’Heisenberg.
Représentation de Schrödinger
Dans la représentation de Schrödinger, ce sont les fonctions d’onde qui dépendent du temps et leur évolution est déterminée par l’équation de Schrödinger :
$$ \mathrm{i} \frac{\partial \psi(\boldsymbol{x}, t)}{\partial t}=\hat{H} \psi(\boldsymbol{x}, t) $$
On accède aux variables dynamiques comme la position et l’impulsion via des opérateurs ($\hat{\boldsymbol{x}}=\boldsymbol{x}$, $\hat{\boldsymbol{p}}=-\mathrm{i} \nabla$) qui agissent sur la fonction d’onde.
On est très loin de la mécanique classique où les variables dynamiques ($\boldsymbol{p}(t)$, $\boldsymbol{x}(t)$,…) dépendent du temps et sont donc décrites par des équations du mouvement. Mais comme aucun “opérateur temps” n’existe en mécanique quantique, il faut se contenter d’un paramètre temporel $t$ que la représentation de Schrödinger confine donc entièrement dans la fonction d’onde.
Pas d’opérateur donnant le temps mais quand même un opérateur d’évolution $\hat{U}(t_2,t_1)$ permettant de faire évoluer une particule de $t_1$ à $t_2$.
$$ \psi\left(t_2\right)=\hat{U}\left(t_2, t_1\right) \psi\left(t_1\right) $$
L’opérateur d’évolution a les propriétés suivantes :
- $\hat{U}\left(t_1, t_1\right)=1$
Rien ne se passe si les instants sont les mêmes. - $\hat{U}\left(t_3, t_2\right) \hat{U}\left(t_2, t_1\right)=\hat{U}\left(t_3, t_1\right)$
Cette relation de composition montre qu'on peut construire une translation temporelle quelconque en multipliant entre elles une multitude de translations temporelles minuscules. - $\displaystyle \mathrm{i} \frac{\mathrm{~d}}{\mathrm{~d} t_2} \hat{U}\left(t_2, t_1\right)=\hat{H} \hat{U}\left(t_2, t_1\right)$
L'opérateur d'évolution lui-même obéit à l'équation de Schrödinger.
Pour le prouver, on part de $\psi\left(t_2\right)=\hat{U}\left(t_2, t_1\right) \psi\left(t_1\right)$ et on dérive par rapport à $t_2$ :
$$ \frac{\mathrm{d} \psi\left(t_2\right)}{\mathrm{d} t_2}=\frac{\mathrm{d} \hat{U}\left(t_2, t_1\right)}{\mathrm{d} t_2} \psi\left(t_1\right) $$
Et en utilisant $\mathrm{i} \frac{\partial \psi(\boldsymbol{x}, t)}{\partial t}=\hat{H} \psi(\boldsymbol{x}, t)$, on obtient ;
$$ \mathrm{i} \frac{\mathrm{~d} \psi\left(t_2\right)}{\mathrm{d} t_2}=\hat{H} \psi\left(t_2\right)=\hat{H} \hat{U}\left(t_2, t_1\right) \psi\left(t_1\right) $$
- $\hat{U}\left(t_1, t_2\right)=\hat{U}^{-1}\left(t_2, t_1\right)$
On prenant l'inverse de l'opérateur d'évolution, on remonte le temps. - $\hat{U}^{\dagger}\left(t_2, t_1\right) \hat{U}\left(t_2, t_1\right)=1,$
L'opérateur d'évolution est unitaire.
Pour $t_2=t_1$, c’est trivial.
Pour $t_2\neq t_1$, montrons que cette composition d’opérateurs est constante (et cette constante vaut 1 par normalisation) :
$$ \begin{aligned} \frac{\mathrm{d}}{\mathrm{~d} t_2}\left[\hat{U}^{\dagger}\left(t_2, t_1\right) \hat{U}\left(t_2, t_1\right)\right] & =\frac{\mathrm{d} \hat{U}^{\dagger}}{\mathrm{d} t_2} U+U^{\dagger} \frac{\mathrm{d} \hat{U}}{\mathrm{~d} t_2} \\ & =-\frac{\hat{U}^{\dagger} \hat{H} \hat{U}}{\mathrm{i}}+\frac{\hat{U}^{\dagger} \hat{H} \hat{U}}{\mathrm{i}}\\ &=0 \end{aligned} $$
où on a utilisé $\frac{\mathrm{d} \hat{U}}{\mathrm{~d} t}=\frac{\hat{H} \hat{U}}{\mathrm{i}}$ et $\frac{\mathrm{d} \hat{U}^{\dagger}}{\mathrm{d} t}=-\frac{\hat{U}^{\dagger} \hat{H}}{\mathrm{i}}$.
Une conséquence directe est que $\hat{U}^\dagger(t_2,t_1)=\hat{U}^{-1}(t_2,t_1)$ ; l’opérateur adjoint est l’opérateur inverse.
La propriété 3 permet d’exprimer explicitement $\hat{U}(t_2,t_1)$ :
$$ \hat{U}\left(t_2, t_1\right)=\mathrm{e}^{-\mathrm{i} \hat{H}\left(t_2-t_1\right)} $$
Ce type d’expression exponentiel cache le développement :
$$ \mathrm{e}^{\hat{A}}=1+\hat{A}+\frac{1}{2!} \hat{A} \hat{A}+\frac{1}{3!} \hat{A} \hat{A} \hat{A}+\ldots $$
Représentation d’Heisenberg
Plutôt que de placer la dépendance temporelle dans la fonction d’onde, dans la représentation d’Heisenberg, ce sont les opérateurs qui la prennent en charge.
Pour passer d’une représentation à l’autre, commençons par écrire la valeur moyenne de l’opérateur $O$ dans l’état $\psi(t)$ :
$$ \langle\hat{O}(t)\rangle=\langle\psi(t)| \hat{O}|\psi(t)\rangle $$
Toutes les représentations doivent s’accorder sur ce résultat.
Utilisons maintenant l’opérateur d’évolution pour ne plus avoir à s’occuper que de l’état à l’instant initial $\psi(0)$ :
$$ \psi(t)=\hat{U}(t, 0) \psi(0)=\mathrm{e}^{-\mathrm{i} \hat{H} t} \psi(0) $$
Et en replaçant $\psi(t)$ dans l’expression de la valeur moyenne :
$$ \langle\psi(t)| \hat{O}|\psi(t)\rangle=\langle\psi(0)| \hat{U}^{\dagger}(t, 0) \hat{O} \hat{U}(t, 0)|\psi(0)\rangle $$
Dans la représentation de Schrödinger, on considère les opérateurs comme indépendants du temps ($\hat{O}_{\mathrm{S}} \equiv \hat{O}$), contrairement aux états ($\left|\psi_{\mathrm{S}}(t)\right\rangle \equiv \hat{U}(t, 0)|\psi(0)\rangle$) de telle sorte que :
$$ \langle\psi(0)| \hat{U}^{\dagger}(t, 0)[\hat{O}] \hat{U}(t, 0)|\psi(0)\rangle=\left\langle\psi_{\mathrm{S}}(t)\right| \hat{O}_{\mathrm{S}}\left|\psi_{\mathrm{S}}(t)\right\rangle $$
Mais en étendant un peu les crochets, on obtient une nouvelle façon de voir les choses où les opérateurs deviennent des objets dynamiques :
$$ \langle\psi(0)|\left[\hat{U}^{\dagger}(t, 0) \hat{O} \hat{U}(t, 0)\right]|\psi(0)\rangle=\left\langle\psi_{\mathrm{H}}\right| \hat{O}_{\mathrm{H}}(t)\left|\psi_{\mathrm{H}}\right\rangle $$
On obtient ainsi la représentation d’Heisenberg où les états sont indépendants du temps ($\psi_{\mathrm{H}} \equiv \psi(0)$), contrairement aux opérateurs :
$$ \hat{O}_{\mathrm{H}}(t) \equiv \hat{U}^{\dagger}(t, 0) \hat{O}_{\mathrm{S}} \hat{U}(t, 0) $$
On retrouve une situation similaire à la mécanique classique avec ses variables dynamiques.
Et pour expliciter la dépendance temporelle de $\hat{O}_H(t)$, on différentie l’équation précédente et on utilise la propriété 3 de l’opérateur d’évolution :
$$ \frac{\mathrm{d} \hat{O}_{\mathrm{H}}(t)}{\mathrm{d} t}=\frac{\mathrm{d} \hat{U}^{\dagger}}{\mathrm{d} t} \hat{O}_{\mathrm{S}} \hat{U}+\hat{U}^{\dagger} \hat{O}_{\mathrm{S}} \frac{\mathrm{~d} \hat{U}}{\mathrm{~d} t}=\frac{1}{\mathrm{i}}\left(-\hat{U}^{\dagger} \hat{H} \hat{O}_{\mathrm{S}} \hat{U}+\hat{U}^{\dagger} \hat{O}_{\mathrm{S}} \hat{H} \hat{U}\right) $$
En utilisant la définition de $\hat{O}_H(t)$ et le fait que $\hat{U}$ et $\hat{H}$ commutent (puisque $\hat{U}$ s’exprime à partir de $\hat{H}$), on obtient l’équation du mouvement d’Heisenberg :
$$ \frac{\mathrm{d} \hat{O}_{\mathrm{H}}(t)}{\mathrm{d} t}=\frac{1}{\mathrm{i} \hbar}\left[\hat{O}_{\mathrm{H}}(t), \hat{H}\right] $$
Les limites de la description du monde par la mécanique quantique
La mécanique quantique “classique” est une description formidable du monde à petite échelle. Mais c’est fondamentalement une description à une particule. Tant qu’on n’est pas embêté par la relativité, ça suffit. Mais les deux résultats suivants témoignent de l’incapacité de la mécanique quantique à une particule à s’accommoder d’un cadre relativiste.
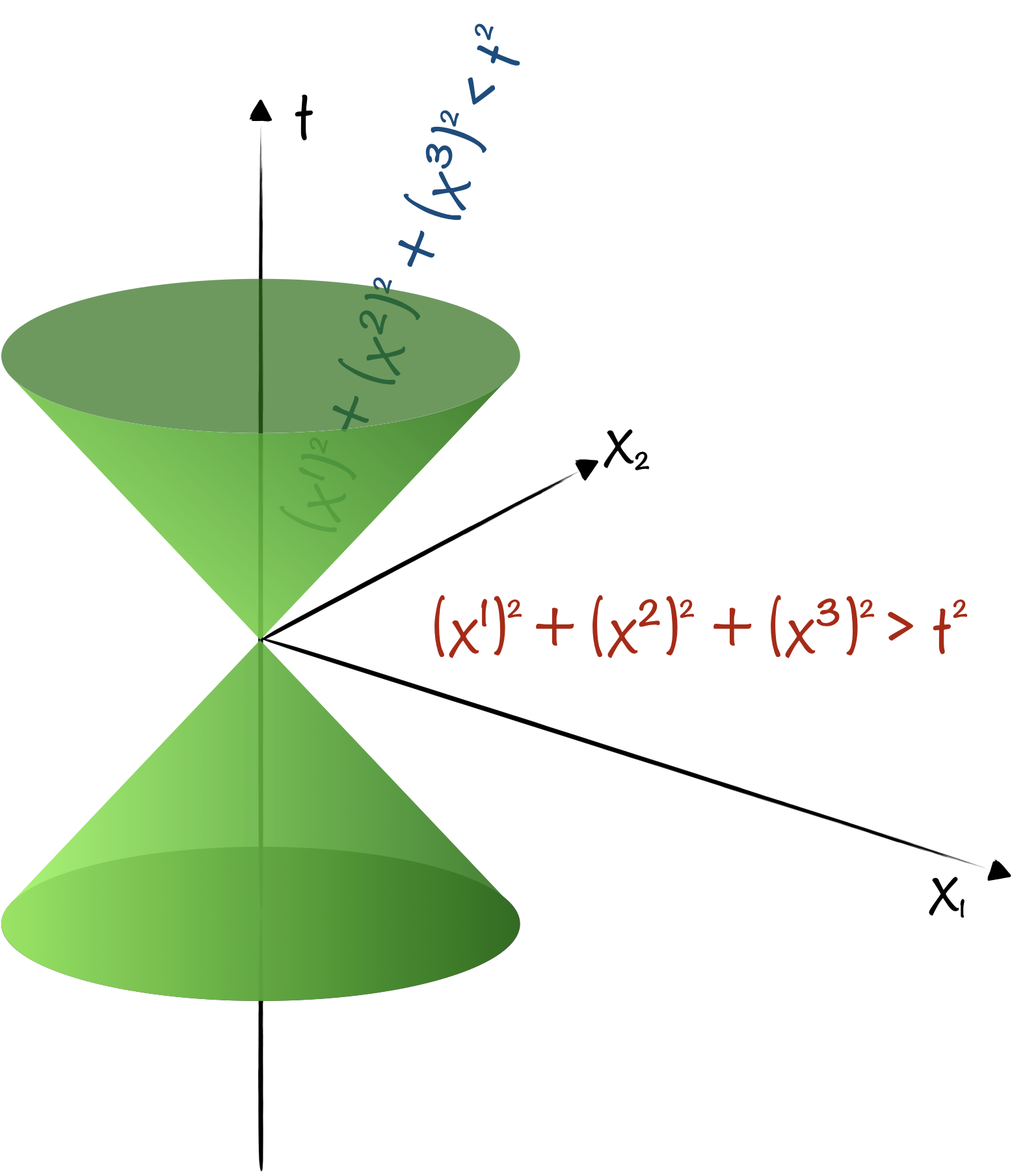
Premier coup dur : la probabilité de trouver la particule en dehors de son cône de lumière n’est pas nulle. En effet, $\langle\boldsymbol{x}| \mathrm{e}^{-\mathrm{i} \hat{H} t}|\boldsymbol{x}=0\rangle$ donne un résultat proportionnel à $\mathrm{e}^{-m|x|}$ pour un intervalle de type espace (tel que $|x|>t$). C’est certes infime pour des grands $|\boldsymbol{x}|$, mais cela reste difficilement acceptable…
Deuxième coup porté : imaginons que l’on cloisonne la particule entre deux murs (des barrières de potentiel) séparés d’une distance bien inférieure à sa longueur d’onde de Compton $\lambda=h m / c$ ($1/m$ en unités naturelles). La minuscule incertitude sur la position ($\Delta x \ll \lambda$) entraîne une incertitude sur l’impulsion telle ($\Delta p \gg 1/\lambda=m$) que l’énergie de la particule devient suffisante pour faire jaillir des paires de particules-antiparticules. La boite devrait alors contenir en moyenne plus d’une particule, situation que la mécanique quantique “classique” n’est pas câblée pour décrire.
Ces objets définis localement (en un point $x$ de l’espace-temps) que sont les champs et plus précisément les champs d’opérateurs $\hat{\phi}(x)$ vont tirer la quantique de ce mauvais pas. Et puisqu’il s’agit de placer au premier plan des opérateurs dynamiques, la représentation d’Heisenberg va se trouver être la représentation idoine.
Pour rendre un champ d’opérateurs compatible avec la relativité, il suffit de s’assurer que des opérateurs éloignés d’un intervalle de type espace commutent ($[\hat{\phi}(x), \hat{\phi}(y)]=0$ si $(x-y)^2<0$). Cela empêche que le résultat de l’une des mesures puisse influer causalement le résultat de l’autre.
Transformations continues
Translations dans l’espace-temps
Pour translater une particule dans l’espace, il nous faut un opérateur $\hat{U}$ qui transforme un état localisé en $\boldsymbol{x}$ en un état localisé en $\boldsymbol{x}+\boldsymbol{a}$ :
$$ \hat{U}(\boldsymbol{a})|\boldsymbol{x}\rangle=|\boldsymbol{x}+\boldsymbol{a}\rangle $$
On suppose ici qu’on a transporté la particule à sa nouvelle place ; on parle alors de point de vue actif.
Faisons maintenant agir l’opérateur sur une fonction d’onde $\psi(x)$ :
$$ \hat{U}(\boldsymbol{a})\psi(\boldsymbol{x})=\psi(\boldsymbol{x}-\boldsymbol{a}) $$
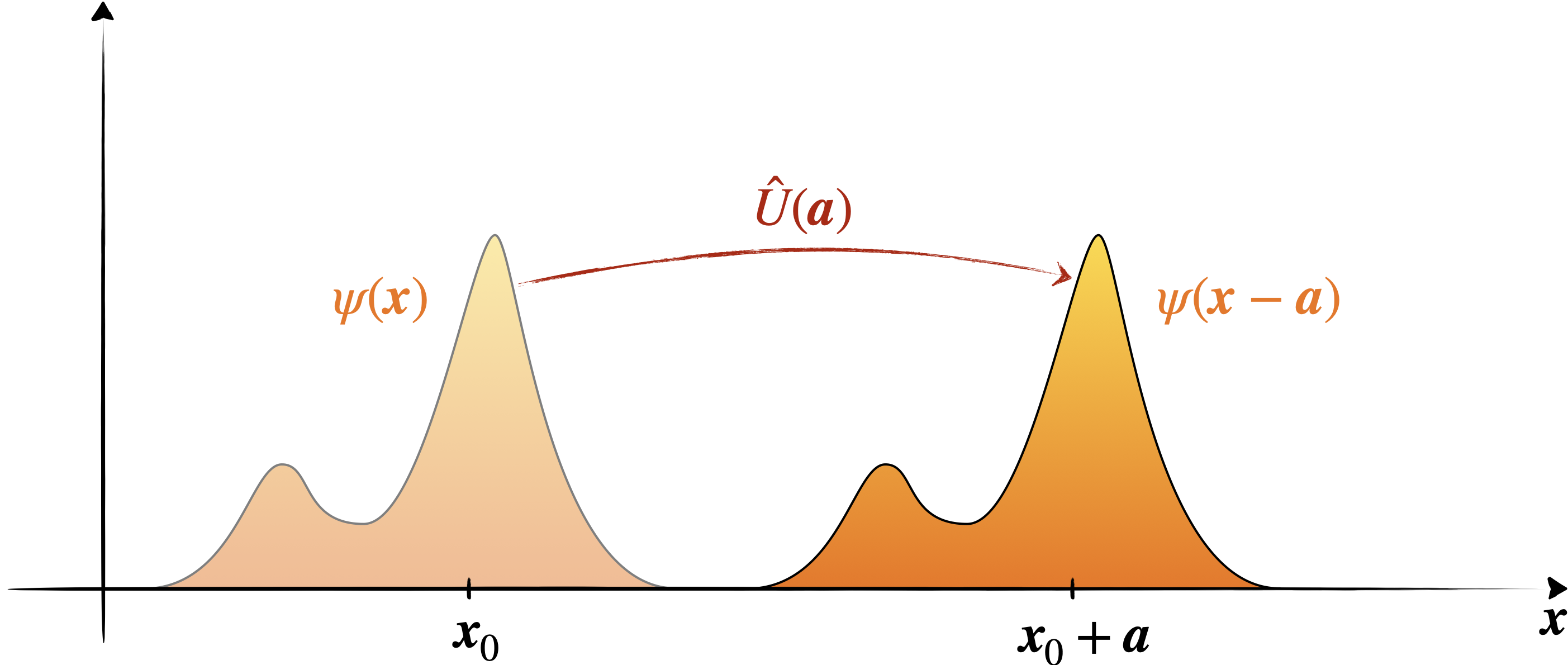
Soit $|\psi\rangle$ l’état décrit par la fonction d’onde $\psi(\boldsymbol{x})=\langle\psi|\boldsymbol{x}\rangle$ et soit $|\phi\rangle=\hat{U}(\boldsymbol{a})|\psi\rangle$, l’état translaté.
$$ \begin{aligned} \phi(\boldsymbol{x}) & =\langle \boldsymbol{x} | \phi\rangle\\ &=\langle \boldsymbol{x} | \hat{U}(\boldsymbol{a})|\psi\rangle\\ &=\int d \boldsymbol{x}^{\prime} \langle \boldsymbol{x} | \hat{U}(\boldsymbol{a}) | \boldsymbol{x}^{\prime}\rangle \langle \boldsymbol{x}^{\prime} | \psi \rangle\\ &=\int d \boldsymbol{x}^{\prime} \langle \boldsymbol{x} | \boldsymbol{x}^{\prime}+\boldsymbol{a} \rangle \langle \boldsymbol{x}^{\prime} | \psi\rangle \\ & =\int d \boldsymbol{x}^{\prime} \delta (\boldsymbol{x}-\boldsymbol{x}^{\prime}-\boldsymbol{a}) \psi (\boldsymbol{x}^{\prime})\\ &=\psi(\boldsymbol{x}-\boldsymbol{a}) \end{aligned} $$
En réécrivant ça $\phi(\boldsymbol{x}+\boldsymbol{a})=\psi(\boldsymbol{x})$, on obtient un moyen simple de se souvenir du signe :
la valeur de la nouvelle fonction d’onde au nouveau point est égale à la valeur de l’ancienne fonction d’onde à l’ancien point.
Propriétés de l’opérateur de translation :
-
$\hat{U}(\boldsymbol{0})=1$
Présence d'un élément neutre. -
$\hat{U}(\boldsymbol{a})\hat{U}(\boldsymbol{b})=\hat{U}(\boldsymbol{a}+\boldsymbol{b})$
Loi de composition. -
$\hat{U}(\boldsymbol{a})^{-1}=\hat{U}(-\boldsymbol{a})$
L'opérateur de translation admet un inverse. -
$\hat{U}(\boldsymbol{a})^{-1}=\hat{U}(\boldsymbol{a})^\dagger$
L'opérateur de translation est unitaire.
Ces propriétés nous montrent que ces transformations forment un groupe et comme chaque élément dépend d’un paramètre continu ($\boldsymbol{a}$) entraînant que le groupe possède un nombre infini d’éléments, il s’agit d’un groupe de Lie.
Un groupe est un ensemble $G$ muni d’une loi de composition interne $\bullet$ associative admettant un élément neutre et, pour chaque élément de l’ensemble, un élément symétrique :
- $\forall a, b \in G, a \bullet b \in G$ (loi de composition interne assurant la fermeture du groupe)
- $\forall a, b, c \in G, a \bullet(b \bullet c)=(a \bullet b) \bullet c$ (associativité)
- $\exists e \in G$ tel que $\forall a \in G, a \bullet e=e \bullet a=a$ (élément neutre)
- $\forall a \in G, \exists a^{-1} \in G$ tel que $a \bullet a^{-1}=a^{-1} \bullet a=e$ (inverse)
Des vieilles notes de lecture d’un autre chouette livre pour en savoir un peu plus sur les groupes discrets.
L’opérateur de translation peut aussi être vu comme la transformation d’un opérateur :
$$ \hat{U}^{\dagger}(\boldsymbol{a}) \hat{\boldsymbol{x}} \hat{U}(\boldsymbol{a})=(\hat{\boldsymbol{x}}+\boldsymbol{a}) . $$
$$ \begin{aligned} \hat{U}(\boldsymbol{a})|\boldsymbol{x}\rangle & =|\boldsymbol{x}+\boldsymbol{a}\rangle \\ \hat{\boldsymbol{x}} U(\boldsymbol{a})|\boldsymbol{x}\rangle & =\hat{\boldsymbol{x}}|\boldsymbol{x}+\boldsymbol{a}\rangle=(\boldsymbol{x}+\boldsymbol{a})|\boldsymbol{x}+\boldsymbol{a}\rangle \\ U^{\dagger}(\boldsymbol{a}) \hat{\boldsymbol{x}} U(\boldsymbol{a})|\boldsymbol{x}\rangle & =(\boldsymbol{x}+\boldsymbol{a}) U^{\dagger}(\boldsymbol{a})|\boldsymbol{x}+\boldsymbol{a}\rangle=(\boldsymbol{x}+\boldsymbol{a})|\boldsymbol{x}\rangle \end{aligned} $$
Imaginons une observable représentée par l’opérateur $\hat{O}$. Si une translation n’a pas d’effet sur la propriété mesurée par cet opérateur, on peut écrire :
$$ \langle\psi(\boldsymbol{x})| \hat{O}|\psi(\boldsymbol{x})\rangle=\langle\psi(\boldsymbol{x})| \hat{U}^{-1}(\boldsymbol{a}) \hat{O} \hat{U}(\boldsymbol{a})|\psi(\boldsymbol{x})\rangle $$
On dit alors que l’opérateur est un invariant et la condition pour qu’un opérateur $\hat{O}$ soit un invariant est donc :
$$ \hat{U}^{-1}(\boldsymbol{a}) \hat{O} \hat{U}(\boldsymbol{a})=\hat{O} $$
Ce qui devient en faisant agir $\hat{U}$ à gauche de chaque membre de l’égalité :
$$ [\hat{O},\hat{U}]=0 $$
L’invariance par rapport à une transformation implique la commutation des opérateurs.
Essayons maintenant d’obtenir une formule explicite pour l’opérateur de translation.
$$ \psi(x-\delta a)=\psi(x)-\frac{\mathrm{d} \psi(x)}{\mathrm{d} x} \delta a+\ldots $$
Ce qu’on peut réécrire au premier ordre, en se rappelant que $\hat{p}=-\mathrm{i} \frac{\mathrm{~d}}{\mathrm{~d} x}$ :
$$ \psi(x-\delta a)=(1-\mathrm{i} \hat{p} \delta a) \psi(x) $$
On dit que l’opérateur $\hat{p}$ est le générateur des translations spatiales. Pour opérer une translation d’une distance $a$, on peut translater de $\delta a$ un grand nombre $N$ de fois :
$$ \begin{aligned} \psi(x-a) & =\lim _{N \rightarrow \infty}(1- \mathrm{i} \hat{p} \delta a)^N \psi(x) \\ & =\mathrm{e}^{-\mathrm{i} \hat{p} a} \psi(x) \end{aligned} $$
Par identification :
$$ \hat{U}(\boldsymbol{a})=\mathrm{e}^{-\mathrm{i} \hat{\boldsymbol{p}} \cdot \boldsymbol{a}} $$
Action de l’opérateur de translation sur un état d’impulsion $|\boldsymbol{q}\rangle :$
$$ \begin{aligned} \hat{U}(\boldsymbol{a})|\boldsymbol{q}\rangle & =\mathrm{e}^{-\mathrm{i} \hat{p} \cdot \boldsymbol{a}}|\boldsymbol{q}\rangle \\ & =\mathrm{e}^{-\mathrm{i} \boldsymbol{q} \cdot \boldsymbol{a}}|\boldsymbol{q}\rangle \end{aligned} $$
Projeté sur l’axe des coordonnées, on obtient bien une fonction d’onde translatée :
$$ \langle\boldsymbol{x}| \hat{U}(\boldsymbol{a})|\boldsymbol{q}\rangle=\langle\boldsymbol{x} | \boldsymbol{q}\rangle \mathrm{e}^{-\mathrm{i} \boldsymbol{q} \cdot \boldsymbol{a}}=\frac{1}{\sqrt{\mathcal{V}}} \mathrm{e}^{\mathrm{i} \boldsymbol{q} \cdot(\boldsymbol{x}-\boldsymbol{a})} $$
L’opérateur d’évolution de la section précédente peut aussi être vu comme un opérateur de translation temporelle.
On peut le reconstruire sur le modèle des translations spatiales en partant d’une petite variation $\delta t_a$ dans la fonction d’onde :
$$ \psi\left(t-\delta t_a\right)=\psi(t)-\frac{\mathrm{d} \psi(t)}{\mathrm{d} t} \delta t_a+\ldots $$
Et comme $\hat{H}=\mathrm{i} \frac{\mathrm{~d}}{\mathrm{~d} t}$, on obtient :
$$ \psi\left(t-\delta t_a\right)=\left(1+\mathrm{i} \hat{H} \delta t_a\right) \psi(t) $$
Ce qui donne finalement :
$$ \hat{U}(t_a)=\mathrm{e}^{\mathrm{i}\hat{H}t_a} $$
On peut dès lors combiner les deux translations en un seul opérateur de translation spatio-temporelle en définissant l’opérateur quadri-impulsion $\hat{p}=(\hat{H}, \hat{\boldsymbol{p}})$ :
$$ \hat{U}(a)=\mathrm{e}^{\mathrm{i} \hat{p} \cdot a}=\mathrm{e}^{\mathrm{i} \hat{H} t_a-\mathrm{i} \hat{\boldsymbol{p}} \cdot \boldsymbol{a}} $$
Rotations
Une matrice de rotation $\mathbf{R}(\boldsymbol{\theta})$ (où $\boldsymbol{\theta}$ est le vecteur dont l’axe est celui de la rotation et la norme est donnée par l’angle) agit sur une grandeur vectorielle comme l’impulsion : $\boldsymbol{p}^{\prime}=\mathbf{R}(\boldsymbol{\theta}) \boldsymbol{p}$. L’opérateur vectoriel associé peut se définir comme :
$$ \left|\boldsymbol{p}^{\prime}\right\rangle=\hat{U}(\boldsymbol{\theta})|\boldsymbol{p}\rangle=|\mathbf{R}(\boldsymbol{\theta}) \boldsymbol{p}\rangle $$
L’opérateur possède à nouveau les propriétés clés attendues pour une telle transformation :
- unitarité : $\hat{U}^{\dagger}(\boldsymbol{\theta}) \hat{U}(\boldsymbol{\theta})=1$
- présence d'un élément neutre : $\hat{U}(0)=1$
- loi de composition interne : $\hat{U}(\boldsymbol{\theta}\_1)\hat{U}(\boldsymbol{\theta}\_2)=\hat{U}(\boldsymbol{\theta}\_{12})$ où $\mathbf{R}(\boldsymbol{\theta}\_{12})=\mathbf{R}(\boldsymbol{\theta}\_1) \mathbf{R}(\boldsymbol{\theta}\_2)$
Preuve de l'unitarité :
$$ \begin{aligned} \hat{U}(\boldsymbol{\theta}) \hat{U}^{\dagger}(\boldsymbol{\theta}) & =\hat{U}(\boldsymbol{\theta})\left(\int \mathrm{d}^3 p|\boldsymbol{p}\rangle\langle\boldsymbol{p}|\right) \hat{U}^{\dagger}(\boldsymbol{\theta}) \\ & =\int \mathrm{d}^3 p|\mathbf{R}(\boldsymbol{\theta}) \boldsymbol{p}\rangle\langle\mathbf{R}(\boldsymbol{\theta}) \boldsymbol{p}|\\ &=\int \mathrm{d}^3 \boldsymbol{p}^{\prime}|\boldsymbol{p}^{\prime}\rangle\langle\boldsymbol{p}^{\prime}|\\ &=1 \end{aligned} $$
Puisque $\boldsymbol{p}^{\prime}=\mathbf{R}(\boldsymbol{\theta}) \boldsymbol{p}$ et $\mathrm{d}^3 p^{\prime}=\mathrm{d}^3 p$ car $\operatorname{det} \mathbf{R}(\boldsymbol{\theta})=1$ par conservation de l’orientation (et donc le jacobien vaut 1).
Ces opérateurs forment un nouveau groupe de Lie appelé le groupe des rotations.
Translations dans l’espace-temps, rotations et boosts de Lorentz et leurs combinaisons sont tous des éléments du groupe de Poincaré et peuvent tous être représentés par des opérateurs unitaires.
La rotation, non plus d’un état, mais d’un opérateur, est donnée par :
$$ \hat{U}^{\dagger}(\boldsymbol{\theta}) \,\hat{\boldsymbol{p}} \,\hat{U}(\boldsymbol{\theta})=\mathbf{R}(\boldsymbol{\theta}) \hat{\boldsymbol{p}} $$
Cherchons là encore à exprimer explicitement l’opérateur en partant d’une petite rotation selon l’axe des $z$ d’une fonction d’onde :
$$ \psi\left(\theta^z-\delta \theta^z\right)=\psi\left(\theta^z\right)-\frac{\mathrm{d} \psi\left(\theta^z\right)}{\mathrm{d} \theta^z} \delta \theta^z+\ldots $$
C’est maintenant l’opérateur moment angulaire qui va jouer le rôle de générateur de la transformation. Et dans notre cas, on utilise le fait que $\hat{J}^z=-\mathrm{i} \frac{\mathrm{~d}}{\mathrm{~d} \theta^z}$ :
$$ \psi\left(\theta-\delta \theta^z\right)=\left(1-\mathrm{i} \hat{J}^z \delta \theta^z\right) \psi\left(\theta^z\right) $$
Et finalement, en répétant $N\rightarrow\infty$ fois l’opération, l’opérateur s’écrit $\hat{U}(\theta^z)=\mathrm{e}^{-\mathrm{i} \hat{J}^z \theta^z}$. Et en généralisant à une rotation quelconque :
$$ \hat{U}(\boldsymbol{\theta})=\mathrm{e}^{-\mathrm{i} \hat{\boldsymbol{J}} \cdot \boldsymbol{\theta}} $$
Représentation des transformations
Transformer un champ est un poil plus compliqué puisqu’il faut à la fois bouger le champ au nouvel endroit et transformer aussi l’objet que le champ produit. Or cet objet peut être de nature différente : scalaire, vectorielle ou spinorielle. Il faut donc pouvoir adapter une même transformation à ces différents objets et c’est la théorie des représentations qui permet cela.
Une représentation d’un groupe, notée $D$, est obtenue en associant chaque élément $g_i$ du groupe $G$ à un opérateur linéaire continu qui agit sur un espace vectoriel. Cette association doit préserver la règle de composition : si $g_1\bullet g_2=g_3$, alors $D(g_1)D(g_2)=D(g_3)$.
En pratique, il s’agit de représenter les éléments du groupe par des matrices.
Exemple des rotations :
Toute rotation $\boldsymbol{R}(\boldsymbol{\theta})$ peut être représentée par une matrice $D(\boldsymbol{\theta})$ qui prend une forme très similaire à l’opérateur :
$$ D(\boldsymbol{\theta})=\mathrm{e}^{-\mathrm{i} \boldsymbol{J} \cdot \boldsymbol{\theta}} $$
$\boldsymbol{J}$ est une matrice carrée et une représentation de l’opérateur $\hat{\boldsymbol{J}}$.
On peut isoler $J^i$ dans l’équation précédente :
$$ J^i=-\left.\frac{1}{\mathrm{i}} \frac{\partial D\left(\theta^i\right)}{\partial \theta^i}\right|_{\theta^i=0} $$
On note souvent les représentations des rotations d’un champ caractérisé par un nombre quantique de moment cinétique $j$, $D^{(j)}(\boldsymbol{\theta})$.
Considérons des rotations autour de l’axe des $z$.
- Une représentation triviale est $D(\theta^z)=1$, et donc $J^z=-\left.\frac{1}{\mathrm{i}} \frac{\partial D\left(\theta^z\right)}{\partial \theta^z}\right|\_{\theta^z=0}=0$. Et par extension, $J^x=J^y=0$. C'est une représentation appropriée pour un champ scalaire puisqu'un scalaire ne peut avoir de moment cinétique. On a donc obtenu la représentation des rotations d'un champ scalaire : $D^{(0}(\boldsymbol{\theta})=1$.
- Pour un champ de spineurs (décrivant des particules de spin $\frac{1}{2}$), la représentation d'une rotation selon l'axe des $z$ peut s'écrire :
$$ D^{1/2}\left(\theta^z\right)=\left(\begin{array}{cc} \mathrm{e}^{-\mathrm{i} \theta^z / 2} & 0 \\ 0 & \mathrm{e}^{\mathrm{i} \theta^z / 2} \end{array}\right) $$
Et donc
$$ J^z=-\left.\frac{1}{\mathrm{i}} \frac{\partial D^{1/2}\left(\theta^z\right)}{\partial \theta^z}\right|_{\theta^z=0}=\frac{1}{2}\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right) $$
-
Pour un champ vectoriel, la représentation matricielle des rotations est plus familière. Pour une rotation selon l'axe $z$, on a :
$$ D^{(1)}(\theta^z)=\mathbf{R}\left(\theta^z\right)=\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos \theta^z & -\sin \theta^z & 0 \\ 0 & \sin \theta^z & \cos \theta^z & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) $$
Ce qui donne :
$$ J^z=-\left.\frac{1}{\mathrm{i}} \frac{\partial \mathbf{R}\left(\theta^z\right)}{\partial \theta^z}\right|_{\theta^z=0}=\mathrm{i}\left(\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) $$
La formule générale pour les éléments de matrice de $D^{(j)}(\boldsymbol{\theta})$ est donnée par :
$$ \begin{aligned} {\left[D^{(j)}(\boldsymbol{\theta})\right]_{m, m^{\prime}} } & =\left\langle j m^{\prime}\right| \hat{U}(\boldsymbol{\theta})|j m\rangle \\ & =\left\langle j m^{\prime}\right| \mathrm{e}^{-\mathrm{i} \hat{\boldsymbol{J}} \cdot \boldsymbol{\theta}}|j m\rangle \end{aligned} $$
On peut ensuite les relations standards de l’opérateur moment cinétique :
$$ \begin{gathered} \hat{J}^z|j \, m\rangle=m|j \, m\rangle, \\ \hat{J}^{ \pm}|j \, m\rangle=\sqrt{(j \mp m)(j+1 \pm m)}|j \,m \pm 1\rangle, \\ \hat{J}^{ \pm}=\hat{J}^x \pm \mathrm{i} \hat{J}^y . \end{gathered} $$
Le point remarquable de toutes ces représentations est qu’elles partagent la même structure algébrique sous-jacente de l’opérateur rotation. Cette algèbre est appelé algèbre de Lie et peut apparaître dès qu’on a un groupe continu.
La continuité entraîne en effet qu’il existe des éléments du groupe arbitrairement proches de l’identité pour lesquels on peut écrire $g(\boldsymbol{\alpha})=1+\mathrm{i} \alpha^i T^i+O(\alpha^2)$ où les $T^i$ sont les générateurs du groupe. L’algèbre de Lie s’exprime alors par le commutateur $\left[T^i, T^j\right]=\mathrm{i} f^{i j k} T^k$ où les $f^{ijk}$ sont appelées constantes de structure.
Pour les rotations $T^i = J^i$ et $f^{ijk}=\varepsilon^{ijk}$.
Transformations d’un champ quantique
Commençons par translater un champ scalaire.
Si on translate à la fois un état et un opérateur du même vecteur $\boldsymbol{a}$, alors rien ne devrait changer :
$$ \langle\boldsymbol{y}| \hat{\phi}(\boldsymbol{x})|\boldsymbol{y}\rangle=\langle\boldsymbol{y}+\boldsymbol{a}| \hat{\phi}(\boldsymbol{x}+\boldsymbol{a})|\boldsymbol{y}+\boldsymbol{a}\rangle $$
Or $|\boldsymbol{y}+\boldsymbol{a}\rangle=\hat{U}(\boldsymbol{a})|\boldsymbol{y}\rangle$, donc $\hat{\phi}(\boldsymbol{x}) = \hat{U}^\dagger (\boldsymbol{a}) \hat{\phi}(\boldsymbol{x}+\boldsymbol{a}) \hat{U}(\boldsymbol{a})$ et par conséquent :
$$ \hat{U}^{\dagger}(\boldsymbol{a}) \hat{\phi}(\boldsymbol{x}) \hat{U}(\boldsymbol{a})=\hat{\phi}(\boldsymbol{x}-\boldsymbol{a}) $$
En passant aux rotations, on doit se rappeler que transformer le champ agit à la fois sur le point sur lequel le champ agit et aussi sur la polarisation du champ. Et cette modification de la polarisation du champ se fait via la représentation appropriée de l’opérateur rotation (pour un champ scalaire, par exemple, $D(\boldsymbol{\theta})=1$).
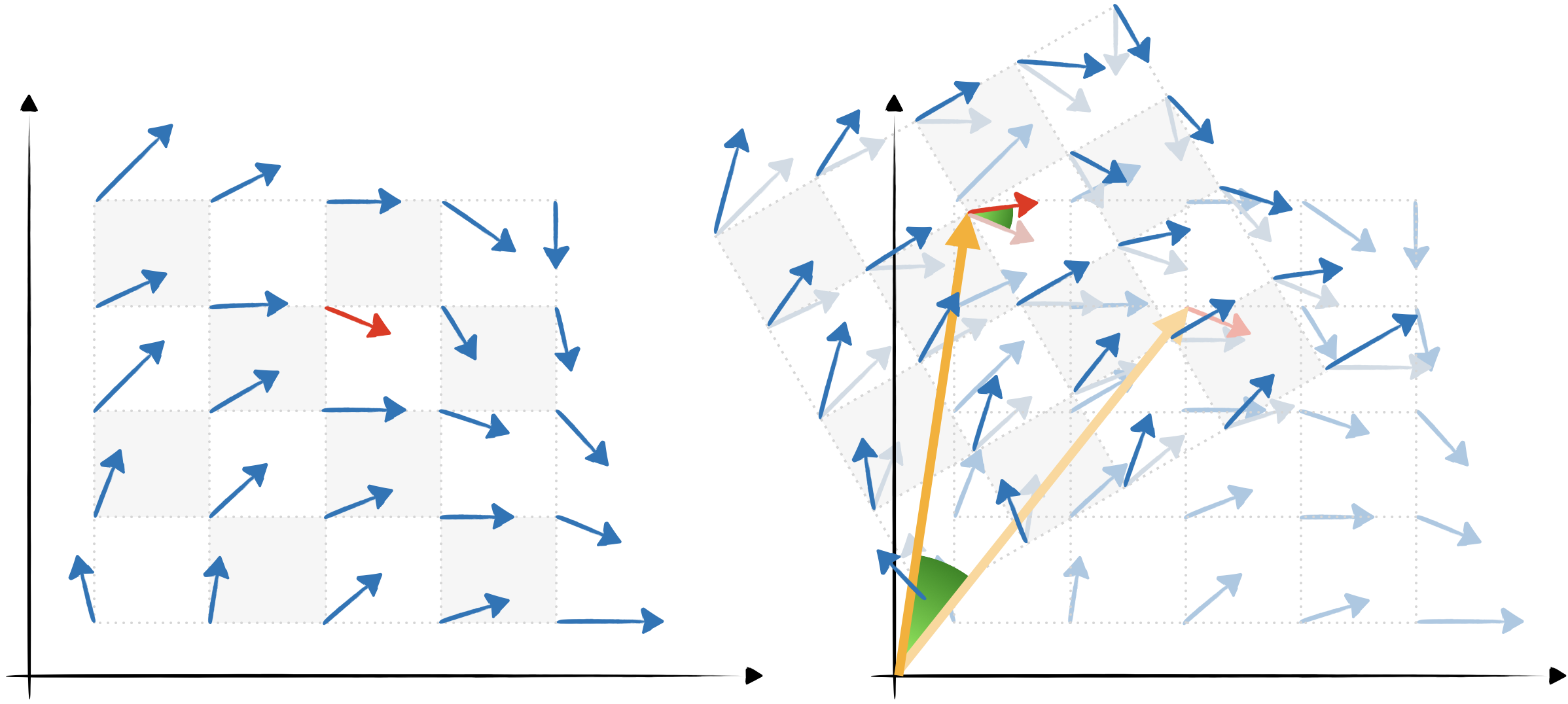
$$ \hat{U}^{\dagger}(\boldsymbol{\theta}) \hat{\boldsymbol{\Phi}}(x) \hat{U}(\boldsymbol{\theta})=D(\boldsymbol{\theta}) \hat{\boldsymbol{\Phi}}\left(\mathbf{R}^{-1}(\boldsymbol{\theta}) x\right) $$
Remarque : dans le dessin, $D(\boldsymbol{\theta}) $ s’occupe de tourner la flèche rouge à sa nouvelle place.
Transformations de Lorentz
Après les translations et les rotations cherchons à exprimer les boosts de Lorentz.
Une transformation de Lorentz selon l’axe $x$ est donnée par $x^{\prime \mu}=\boldsymbol{\Lambda}\left(\beta^1\right)_{\;\nu}^\mu x^\nu$ où :
$$ \boldsymbol{\Lambda}\left(\beta^1\right)=\left(\begin{array}{cccc} \gamma^1 & \beta^1 \gamma^1 & 0 & 0 \\ \beta^1 \gamma^1 & \gamma^1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) $$
Cette transformation connecte deux référentiels inertiels en mouvement relatif avec une vitesse $v=c\beta^1$ selon $x$. En introduisant la rapidité $\phi^i$ définie par $\tanh \phi^i=\beta^i$, la matrice devient :
$$ \boldsymbol{\Lambda}\left(\phi^1\right)=\left(\begin{array}{cccc} \cosh \phi^1 & \sinh \phi^1 & 0 & 0 \\ \sinh \phi^1 & \cosh \phi^1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) $$
Introduisons un opérateur pour cette transformation dans l’espace de Hilbert :
$$ \hat{U}(\boldsymbol{\phi})|\boldsymbol{p}\rangle=|\boldsymbol{\Lambda}(\boldsymbol{\phi}) \boldsymbol{p}\rangle $$
Et sur le modèle des rotations, donnons une forme générale matricielle pour les représentations de la transformation de Lorentz :
$$ D(\phi)=\mathrm{e}^{\mathrm{i} \boldsymbol{K} \cdot \boldsymbol{\phi}} $$
Les générateurs de la transformation sont donnés par :
$$ K^i=\left.\frac{1}{\mathrm{i}} \frac{\partial D\left(\phi^i\right)}{\partial \phi^i}\right|_{\phi^i=0} $$
Un champ quantique se transforme sous l’action d’un boost comme :
$$ \hat{U}^{\dagger}(\boldsymbol{\phi}) \hat{\boldsymbol{\Phi}}(x) \hat{U}(\boldsymbol{\phi})=D(\boldsymbol{\phi}) \hat{\boldsymbol{\Phi}}\left(\boldsymbol{\Lambda}^{-1}(\boldsymbol{\phi}) x\right) $$
Enfin, en jouant avec un jeu de générateurs, on obtient la surprenante relation de commutation suivante :
$$ \left[K^1, K^2\right]=K^1 K^2-K^2 K^1=-\mathrm{i} J^3 $$
La différence entre un boost selon les $x$ suivi d’un boost selon les $y$ et un boost selon les $y$ suivi d’un boost selon les $x$ est une rotation autour des $z$ !
Mathématiquement, cela implique que l’algèbre de Lie des transformations de Lorentz n’est pas fermée et que ses générateurs ne forment pas un groupe.
En généralisant, les relations de commutations s’écrivent :
$$ \left[J^i, K^j\right]=\mathrm{i} \varepsilon^{i j k} K^k $$
Pris ensemble, les boosts et les rotations forment une algèbre de Lie fermée et c’est ce groupe élargi qu’on appelle le groupe de Lorentz. Et de fait, une transformation générale de Lorentz s’écrit :
$$ D(\boldsymbol{\theta}, \boldsymbol{\phi})=\mathrm{e}^{-\mathrm{i}(\boldsymbol{J} \cdot \boldsymbol{\theta}-\boldsymbol{K} \cdot \boldsymbol{\phi})} $$
Les transformations $L$ du groupe de Lorentz sont l’ensemble des transformations linéaires de $\mathbb{R}^{1,3}$ qui préservent la forme bilinéaire de Lorentz (ou pseudo-norme de Minkowski) : $(L(x),L(y))=(x,y)$
Et en ajoutant les translations à la fête, on obtient le groupe de Poincaré.
Symétrie
Invariance et conservation
Une quantité est invariante lorsqu’elle garde la même valeur après une transformation. On dit alors qu’elle présente une certaine symétrie. Un cylindre par exemple est invariant par rotation autour de son axe et on dit alors qu’il possède une symétrie de rotation autour de cet axe.
Une quantité est conservée lorsqu’elle garde la même valeur avant et après un évènement. Dans une collision entre particules par exemple, la quadri-impulsion est conservée dans un référentiel donné.
Ce sont ces deux notions différentes que le théorème de Noether lie entre elles en stipulant qu’une invariance conduit à une loi de conservation.
Paramétrons par une quantité $\lambda$ les variations du champ $\phi(x^\mu)$ soumis à une transformation continue.
Pour une transformation infinitésimale, on va noter :
$$ D \phi=\left.\frac{\partial \phi}{\partial \lambda}\right|_{\lambda=0} $$
de telle façon que le changement infinitésimal $\delta\phi$ du champ induit par $\delta\lambda$ puisse se noter :
$$ \delta \phi=D \phi \delta \lambda $$
Pour une translation d’un quadrivecteur $a^\mu$, par exemple, on peut écrire :
$$ \phi\left(x^\mu\right) \rightarrow \phi\left(x^\mu+\lambda a^\mu\right) $$
Et en posant $y^\mu=x^\mu+\lambda a^\mu$, on obtient :
$$ \frac{\partial \phi}{\partial \lambda}=\frac{\partial \phi}{\partial y^\mu} \frac{\partial y^\mu}{\partial \lambda}=\frac{\partial \phi}{\partial y^\mu} a^\mu $$
Et en prenant la limite $\lambda\rightarrow 0$, on a finalement :
$$ D \phi=a^\mu \partial_\mu \phi $$
Théorème de Noether
Considérons une petite variation du champ $\phi(x)\rightarrow\phi(x)+\delta\phi(x)$ où $\delta\phi(x) = 0$ sur les bords de la région d’espace-temps considérée (ce sont les conditions aux limites de Dirichlet imposant un champ fixe sur les bords permettant d’avoir un principe variationnel bien défini).
La petite variation de la densité lagrangienne $\mathcal{L}$ s’écrit :
$$ \delta \mathcal{L}=\frac{\partial \mathcal{L}}{\partial \phi} \delta \phi+\frac{\partial \mathcal{L}}{\partial\left(\partial_\mu \phi\right)} \delta\left(\partial_\mu \phi\right) $$
Posons :
$$ \Pi^\mu(x)=\frac{\partial \mathcal{L}}{\partial\left(\partial_\mu \phi\right)} $$
$\Pi^\mu(x)$ est la densité d’impulsion.
C’est une généralisation quadrivectorielle du moment conjugué $\pi(x)=\delta \mathcal{L} / \delta \dot{\phi}$. Et d’ailleurs, le moment conjugué est la composante temporelle de la densité d’impulsion : $\Pi^0(x)=\pi(x)$.
La variation de la densité lagrangienne peut maintenant s’écrire :
$$ \delta \mathcal{L}=\frac{\partial \mathcal{L}}{\partial \phi} \delta \phi+\Pi^\mu \delta\left(\partial_\mu \phi\right) $$
En utilisant $\delta\left(\partial_\mu \phi\right)=\partial_\mu(\delta \phi)$ et $\partial_\mu\left(\Pi^\mu \delta \phi\right)=\Pi^\mu \partial_\mu(\delta \phi)+\left(\partial_\mu \Pi^\mu\right) \delta \phi$, on obtient :
$$ \delta \mathcal{L}=\left(\frac{\partial \mathcal{L}}{\partial \phi}-\partial_\mu \Pi^\mu\right) \delta \phi+\partial_\mu\left(\Pi^\mu \delta \phi\right) $$
Supposons que l’action n’est pas modifiée par la transformation :
$$ \begin{aligned} \delta S &= \int \mathrm{d}^4 x\, \delta \mathcal{L}\\ &=\int \mathrm{d}^4 x\left(\frac{\partial \mathcal{L}}{\partial \phi}-\partial_\mu \Pi^\mu\right) \delta \phi+\cancel{\int \mathrm{d}^4 x\, \partial_\mu\left(\Pi^\mu \delta \phi\right)}\\ &=0 \end{aligned} $$
Pourquoi $\int \mathrm{d}^4 x\, \partial_\mu\left(\Pi^\mu \delta \phi\right)=0$ ?
Le théorème de la divergence (Gauss-Ostrogradski) nous dit que la variation d’une quantité dans un volume vaut le flux de cette quantité à travers les parois du volume :
$$ \int_\mathcal{V} \mathrm{d}^4 x\, \partial_\mu\left(\Pi^\mu \delta \phi\right) = \int_\mathcal{\partial V} \mathrm{d}\mathcal{A} \ n_\mu \left(\Pi^\mu \delta \phi\right) $$
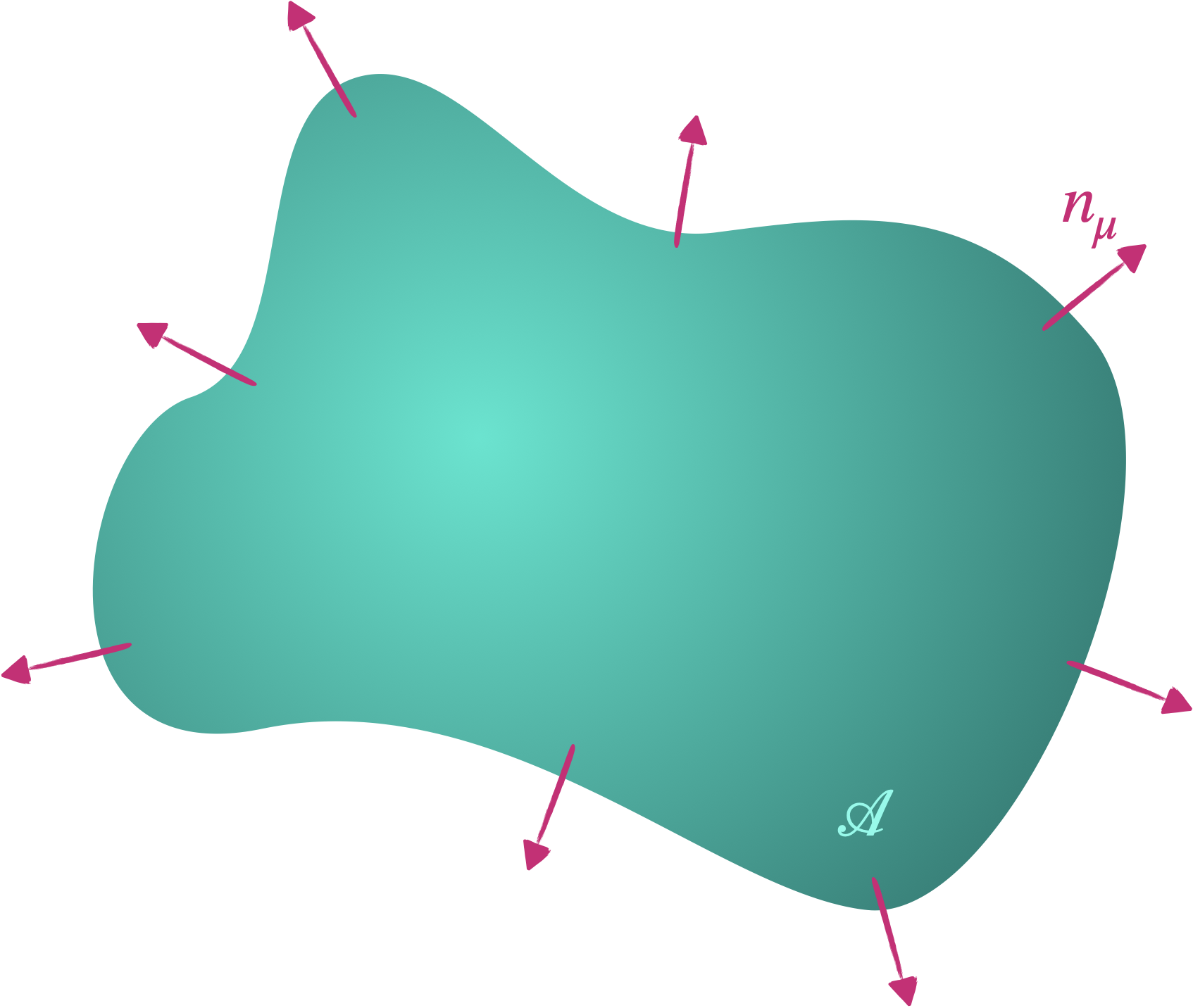
où $n_\mu$ est le vecteur normal à la surface $\mathcal{A}$ qui délimite le volume d’intégration.
Or, comme stipulée plus haut, les variations du champ $\delta\phi$ s’évanouissent sur la frontière.
Par conséquent, on obtient :
$$ \frac{\partial \mathcal{L}}{\partial \phi}=\partial_\mu \Pi^\mu $$
C’est l’équation d’Euler-Lagrange.
Partons maintenant du fait que le champ respecte l’équation du mouvement :
$$ \delta\mathcal{L}=\cancel{\left(\frac{\partial \mathcal{L}}{\partial \phi}-\partial_\mu \Pi^\mu\right) \delta \phi}+\partial_\mu\left(\Pi^\mu \delta \phi\right) $$
En utilisant $\delta \phi=D \phi \delta \lambda$, on obtient :
$$ \delta \mathcal{L}=\partial_\mu\left(\Pi^\mu D \phi\right) \delta \lambda $$
Comme la transformation est sensée être une symétrie du système, son action doit restée inchangée. Cela implique une densité lagrangienne inchangée à la quadri-divergence d’une fonction $W^\mu(x)$ près :
$$ \delta \mathcal{L}=\left(\partial_\mu W^\mu\right) \delta \lambda $$
En effet, l’intégration sur l’espace d’une divergence totale va donner une constante. L’action sera donc la même à une constante près, ce qui sera sans effet sur ses variations (de même qu’en mécanique des particules, le lagrangien est défini à une dérivée totale du temps près).
Finalement, une action stationnaire implique :
$$ \partial_\mu\left(\Pi^\mu D \phi-W^\mu\right)=0 $$
Ou encore $\partial_\mu J_{\mathrm{N}}^\mu=0$ où
$$ J_{\mathrm{N}}^\mu(x)=\Pi^\mu(x) D \phi(x)-W^\mu(x) $$
est le courant de Noether.
Le courant de Noether est donc conservé localement.
Théorème de Noether :
Si une transformation de symétrie continue $\phi\rightarrow\phi+D\phi$ ne change $\mathcal{L}$ que par l’addition d’une quadridivergence ($D\mathcal{L}=\partial_\mu W^\mu$) pour un $\phi$ arbitraire, alors cela implique l’existence d’un courant $J_{\mathrm{N}}^\mu(x)=\Pi^\mu(x) D \phi(x)-W^\mu(x)$.
Si $\phi$ obéit aux équations du mouvement, alors le courant est conservé : $\partial_\mu J_{\mathrm{N}}^\mu=0$.
Les champs conservés donnent naissance à des charges conservées $Q_{\mathrm{N}}=\int J_{\mathrm{N}}^\mu \,\mathrm{d} \mathcal{A}_\mu$ aussi appelées charges de Noether.
En effet, si on fixe le temps, la “surface” d’intégration devient le volume tridimensionnel et donc : $Q_{\mathrm{N}}=\int \mathrm{d}^3 x J_{\mathrm{N}}^0$ où $J^0_N$ est la composante temporelle (normale à la surface).
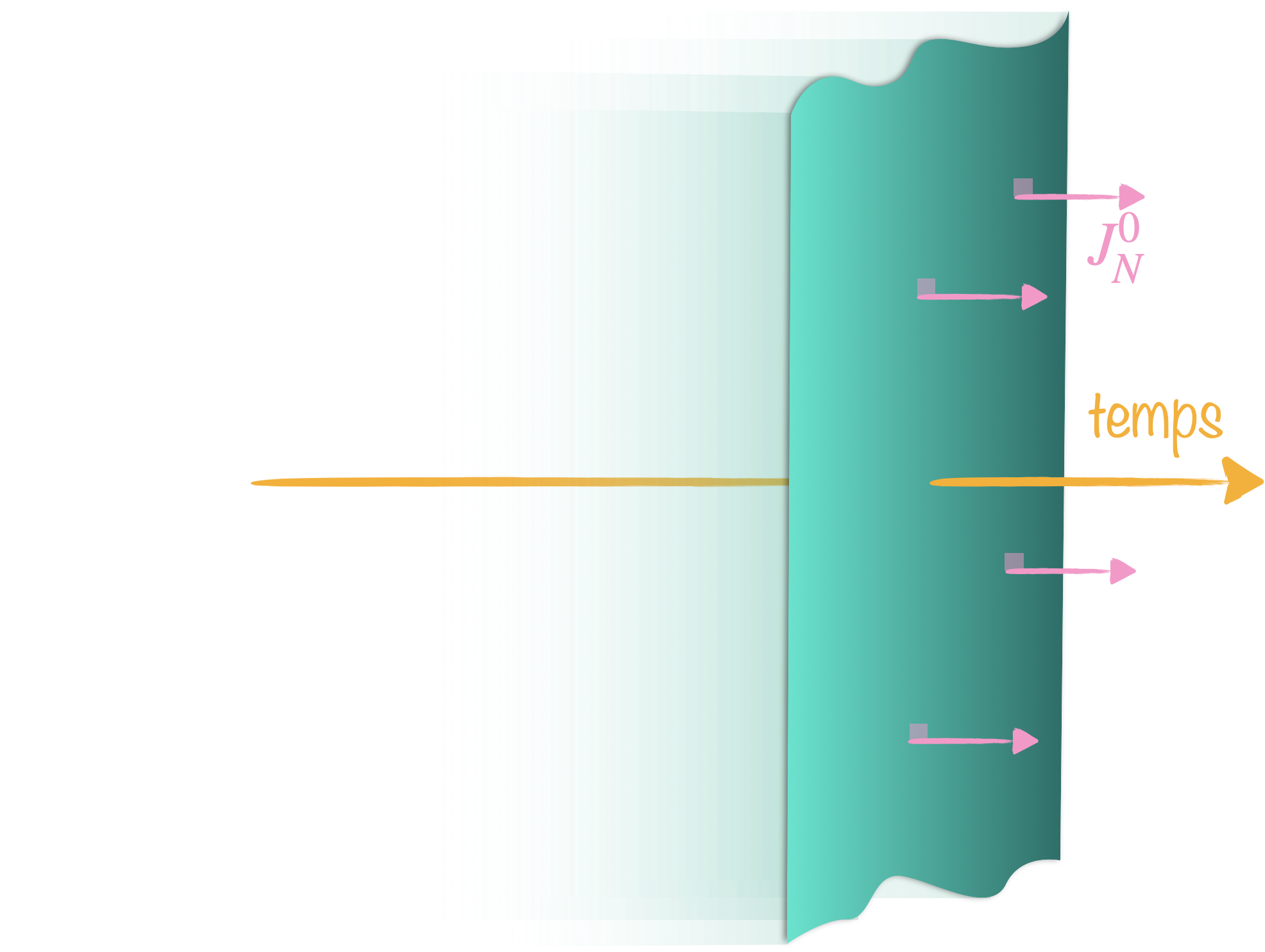
Et comme $\partial_\mu J^\mu_N=0$,
$$ \int \mathrm{d}^3 x\left(\partial_\mu J_{\mathrm{N}}^\mu\right)=\int \mathrm{d}^3 x\left(\partial_0 J_{\mathrm{N}}^0+\partial_k J_{\mathrm{N}}^k\right)=0 $$
En utilisant le théorème de la divergence, le second terme devient :
$$ \int \mathrm{d}^3 x \,\partial_k J_{\mathrm{N}}^k=\int \mathrm{d} \mathcal{A}_k J_{\mathrm{N}}^k $$
Et il disparaît si le volume est assez grand.
On a donc finalement :
$$ \int \mathrm{d}^3 x\, \partial_0 J_{\mathrm{N}}^0=\frac{\mathrm{d} Q_{\mathrm{N}} }{ \mathrm{d} t} = 0 $$
Ça correspond bien à une charge conservée.
Recette pour trouver des charges conservées à partir du théorème de Noether :
- déterminer $D \phi=\left.\frac{\partial \phi}{\partial \lambda}\right|_{\lambda \rightarrow 0}$
- déterminer $\Pi^\mu(x)=\frac{\partial \mathcal{L}}{\partial\left(\partial_\mu \phi\right)}$
- déterminer $\partial_\mu W^\mu=D \mathcal{L}$
- écrire $J_{\mathrm{N}}^\mu=D \phi \Pi^\mu-W^\mu$
- déterminer $Q_{\mathrm{N}}=\int \mathrm{d}^3 x J_{\mathrm{N}}^0$
Application : translations de l’espace-temps
Supposons une translation de l’espace-temps $x^{\prime \mu}=x^\mu+a^\mu$ qui nous donne $D \phi=a^\mu \partial_\mu \phi$. On a aussi $D \mathcal{L}=a^\mu \partial_\mu \mathcal{L}=\partial_\mu\left(a^\mu \mathcal{L}\right)$.
On reconnait alors que $D \mathcal{L}=\partial_\mu W^\mu$ avec $W^\mu=a^\mu \mathcal{L}$. Le courant conservé s’en déduit :
$$ \begin{aligned} J_{\mathrm{N}}^\mu & =\Pi^\mu D \phi-W^\mu \\ & =\Pi^\mu a^\nu \partial_\nu \phi-a^\mu \mathcal{L} \\ & =a^\nu\left[\Pi^\mu \partial_\nu \phi-\delta_\nu^\mu \mathcal{L}\right] \\ & =a_\nu T^{\mu \nu} \end{aligned} $$
où $T^{\mu \nu}=\Pi^\mu \partial^\nu \phi-g^{\mu \nu} \mathcal{L}$ est le tenseur énergie-impulsion.
La charge conservée correspondante peut s’écrire :
$$ P^\alpha=\int \mathrm{d}^3 x \,T^{0 \alpha} $$
La composante temporelle de cette charge est :
$$ P^0=\int \mathrm{d}^3 x \,T^{00}=\int \mathrm{d}^3 x[\pi(x) \dot{\phi}(x)-\mathcal{L}(x)]=\int \mathrm{d}^3 x\, \mathcal{H} $$
On reconnaît l’énergie du champ (on a utilisé $g^{00} = 1$).
Et les composantes spatiales nous donnent :
$$ P^k=\int \mathrm{d}^3 x\, T^{0 k}=\int \mathrm{d}^3 x\, \pi(x) \partial^k \phi(x) $$
On reconnaît là l’impulsion du champ (on a utilisé $g^{0k}=0$).
Un champ symétrique par rapport aux translations voit son énergie et son impulsion conservées.
Petit article de Quantamagazine sur le théorème de Noether.
Symétries internes
Pour des champs plus complexes que des champs scalaires réels, en plus des symétries de l’espace-temps, il faudra se préoccuper de la façon dont les symétries affecte les champ eux-mêmes. On verra par exemple un peu plus loin que la symétrie $U(1)$ d’un champ scalaire complexe entraîne la conservation du nombre de particules !