Théorie quantique des champs – Partie 1
Notes de lecture du livre Quantum field theory for the gifted amateur de Thomas Lancaster et Stephen Blundell.
Les oscillateurs harmoniques
Une vidéo vieille comme tout sur l’oscillateur harmonique quantique qui traite pas mal des points de ce chapitre :
Première quantification : les particules se comportent comme des ondes.
Seconde quantification : les ondes se comportent comme des particules.
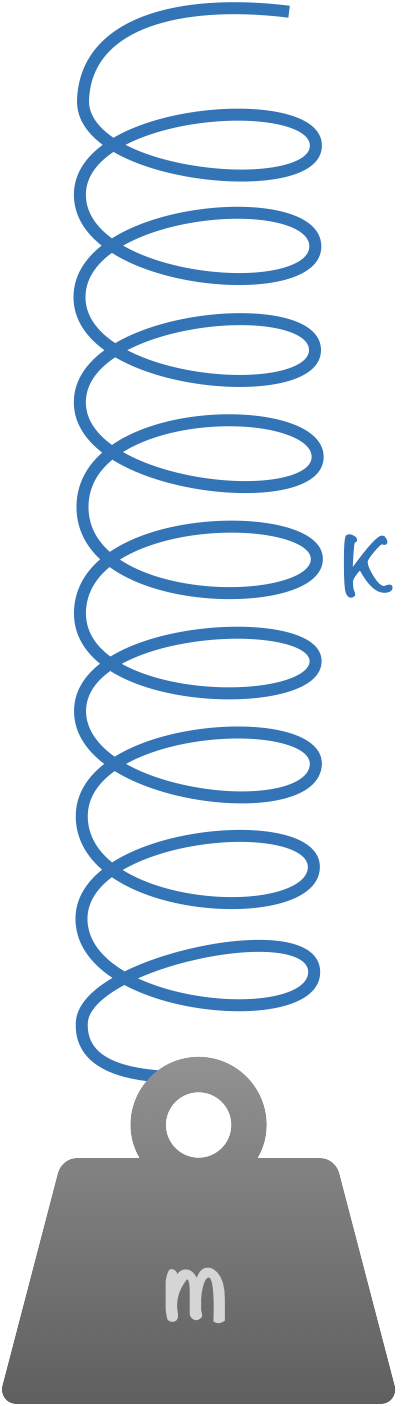
Partons d’une masse $m$ accrochée à un ressort de constante de raideur $K$. La quantité de mouvement de la masse est donnée par $p=m\dot{x}$. L’énergie totale $E$ vaut la somme de l’énergie cinétique $p^2/2m$ et de l’énergie potentielle $\frac{1}{2}Kx^2$.
En mécanique quantique, on remplace $p$ par l’opérateur impulsion $-i\hbar\partial /\partial x$ et on obtient alors l’équation de Schrödinger d’un oscillateur harmonique :
$$\left(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+\frac{1}{2}K x^2\right)\psi=E\psi$$
Les solutions sont données par :
$$\psi_n(\xi)=\frac{1}{\sqrt{2^n n!}}\left(\frac{m\omega}{\pi\hbar}\right)^{1/4}H_n(\xi)\rm{e}^{-\xi^2/2}$$
où les $H_n(\xi)$ sont des polynômes de Hermite et où $\xi=\sqrt{m\omega/\hbar x}$
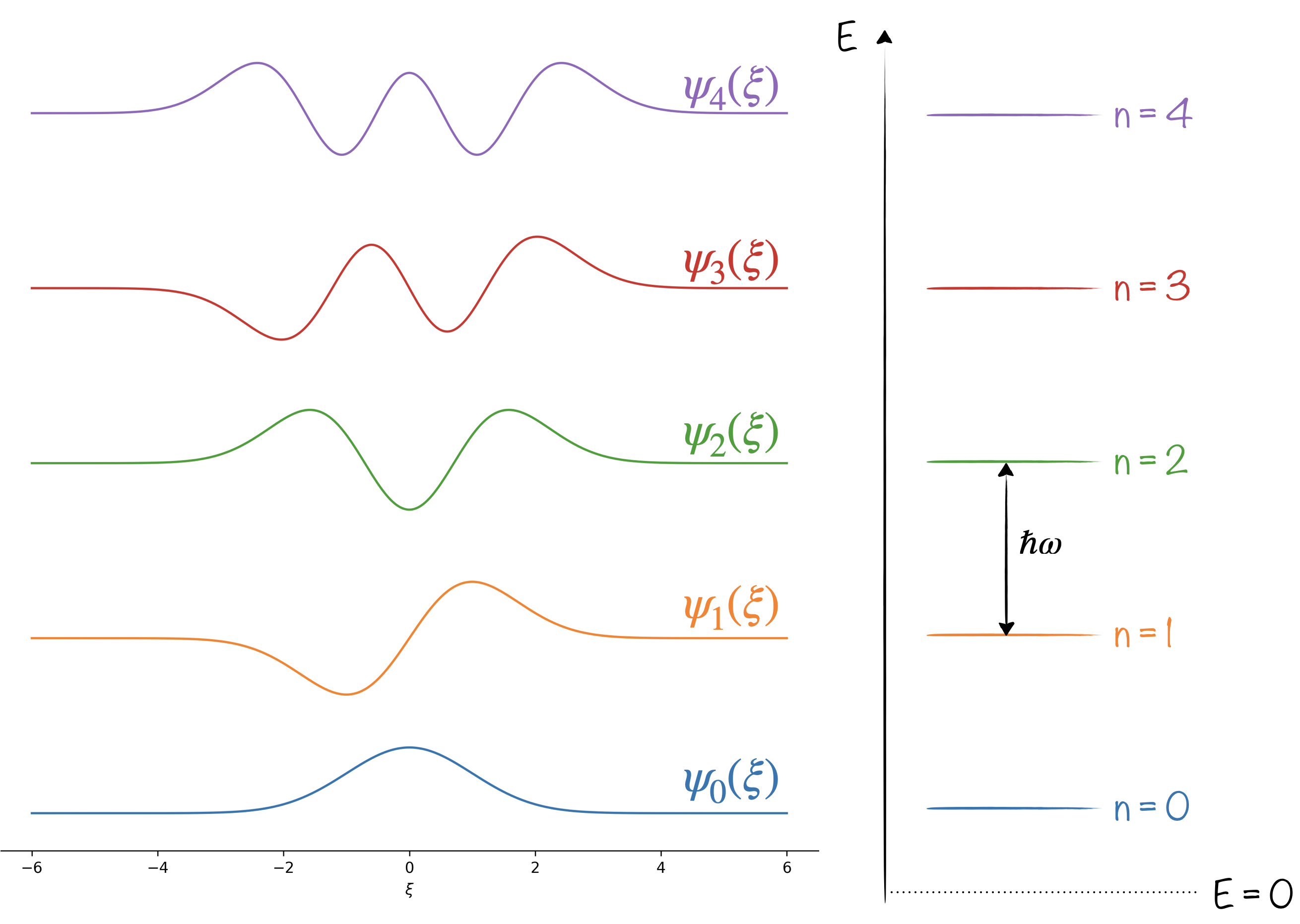
Si ces fonctions propres ressemblent pas mal à des ondes, les valeurs propres $E_n=\left(n+\frac{1}{2}\right)\hbar\omega$ (avec $\omega=\sqrt{K/m}$) se rangent, elles, plutôt du côté particules. On remarque que pour $n=0$, l’énergie n’est pas nulle mais vaut $\hbar\omega/2$. C’est l’énergie de point zéro.
Ajouter un quantum d’énergie $\hbar\omega$ permet de monter d’un barreau l’échelle des énergies, ce que l’on a bien envie de modéliser par l’absorption d’une particule. On peut formaliser ça élégamment (et sans se salir les mains avec les polynômes de Hermite).
On part de l’Hamiltonien de l’oscillateur harmonique :
$$\hat{H}=\frac{\hat{p}^2}{2m}+\frac{1}{2}m\omega^2\hat{x}^2$$
où on a réexprimé la constante de raideur : $K=m\omega^2$.
L’Hamiltonien semble vouloir être factorisé en $\frac{1}{2}m\omega^2\left(\hat{x}-\frac{\mathrm{i}}{m\omega}\hat{p}\right)\left(\hat{x}+\frac{\mathrm{i}}{m\omega}\hat{p}\right)$, mais un problème se dresse : $\hat{x}$ et $\hat{p}$ ne commutent pas ! En effet, $\left[\hat{x},\hat{p}\right]\equiv \hat{x}\hat{p}-\hat{p}\hat{x}=\mathrm{i}\hbar$.
Par conséquent :
Les deux opérateurs $\hat{x}-\frac{\mathrm{i}}{m\omega}\hat{p}$ et $\hat{x}+\frac{\mathrm{i}}{m\omega}\hat{p}$ semblent voués à jouer un rôle important dans cette histoire. Ils sont adjoints l’un de l’autre (puisque $\hat{x}$ et $\hat{p}$ sont hermitiens) ce qui leur interdit d’être eux-mêmes hermitiens et donc de correspondre à une quelconque observable.
Après un petit toilettage, introduisons les opérateurs d’échelle :
$$\hat{a}=\sqrt{\frac{m\omega}{2\hbar}}\left(\hat{x}+\frac{\mathrm{i}}{m\omega}\hat{p}\right)$$
$$\hat{a}^\dagger=\sqrt{\frac{m\omega}{2\hbar}}\left(\hat{x}-\frac{\mathrm{i}}{m\omega}\hat{p}\right)$$
$$[\hat{a},\hat{a}^\dagger]=1$$
On peut inverser les définitions de $\hat{a}$ et $\hat{a}^\dagger$ pour obtenir :
$$\hat{x}=\sqrt{\frac{\hbar}{2m\omega}}\left(\hat{a}+\hat{a}^\dagger\right)$$
$$\hat{p}=-\mathrm{i}\sqrt{\frac{\hbar m \omega}{2}}\left(\hat{a}-\hat{a}^\dagger\right)$$
Et l’Hamiltonien devient :
$$\hat{H}=\hbar\omega\left(\hat{a}^\dagger\hat{a}+\frac{1}{2}\right)$$
Appelons $|n\rangle$ un état propre de $\hat{a}^\dagger\hat{a}$ pour une valeur propre $n$. Alors $|n\rangle$ sera aussi vecteur propre de $\hat{H}$ mais pour une valeur propre $\hbar\omega(n+\frac{1}{2})$. Si $n$ vaut 0, 1, 2, …., on aura bien retrouvé les valeurs propres d’un oscillateur harmonique !
Montrons d’abord que $n≥0$ :
$$n=\langle n|\hat{a}^\dagger\hat{a}|n\rangle = |\hat{a}|n\rangle|^2≥0$$
Montrons ensuite que $n$ ne prend que des valeurs entières.
On commence par définir l’opérateur nombre de quantas de vibration $\hat{n} = \hat{a}^\dagger\hat{a}$. On a alors $\hat{n}|n\rangle = n|n\rangle$.
Nombre de quoi ? $n$ correspond au numéro du barreau d’échelle atteint et donc au nombre de quanta d’énergie $\hbar\omega$ qu’il a fallut ajoutés au système dans son état fondamental.
On peut réécrire l’Hamiltonien $\hat{H}=\hbar\omega\left(\hat{n}+\frac{1}{2}\right)$. Et donc $\hat{H}|n\rangle = \left(\hat{n}+\frac{1}{2}\right) \hbar\omega |n\rangle$. $|n\rangle$ est ainsi un raccourci simple pour les vilains $\psi_n(\xi)$.
De $[\hat{a},\hat{a}^\dagger]=1$, on déduit $\hat{a}\hat{a}^\dagger = 1 +\hat{a}^\dagger\hat{a}=1+\hat{n}$ et donc $\hat{n}\hat{a}^\dagger|n\rangle = \hat{a}^\dagger\hat{a}\hat{a}^\dagger|n\rangle=\hat{a}^\dagger(1+\hat{n})|n\rangle=(n+1)\hat{a}^\dagger|n\rangle$. Par conséquent, $\hat{a}^\dagger|n\rangle$ est un état propre de $\hat{H}$ pour une valeur propre un rang au-dessus de celle de $|n\rangle$. $\hat{a}^\dagger$ a donc pour effet d’ajouter un quantum d’énergie ! C’est l’opérateur de création.
En utilisant la relation de commutation $[\hat{n},\hat{a}]=\hat{n}\hat{a}-\hat{a}\hat{n}=\hat{a}^\dagger\hat{a}\hat{a}-{\color{#970E53}\hat{a}\hat{a}^\dagger}\hat{a}=\hat{a}^\dagger\hat{a}\hat{a}-{\color{#970E53}(1+\hat{a}^\dagger\hat{a})}\hat{a}=-\hat{a}$, on obtient $\hat{n}\hat{a}|n\rangle = (-\hat{a}+\hat{a}\hat{n})|n\rangle=(n-1)\hat{a}|n\rangle$.
$\hat{a}|n\rangle$ est un état propre de $\hat{H}$ pour une valeur propre un rang en-dessous de celle de $|n\rangle$. $\hat{a}$ fait donc descendre d’un étage. C’est l’opérateur d’annihilation.
En appliquant de manière répétée l’opérateur $\hat{a}$ à $|n\rangle$, on pourrait finir avec une énergie négative, ce qui semble physiquement blasphématoire. Il faut donc qu’il existe un état fondamental $|0\rangle$ tel que $\hat{n}|0\rangle = 0$.
Et en appliquant maintenant $\hat{a}^\dagger$ depuis $|0\rangle$, on se retrouve bien avec des valeurs de $n$ entières !
Après normalisation, on obtient :
$$\hat{a}|n\rangle = \sqrt{n}|n-1\rangle$$
$$\hat{a}^\dagger|n\rangle = \sqrt{n+1}|n+1\rangle$$
Preuve :
On a montré que $\hat{a}|n\rangle$ est proportionnel à $|n-1\rangle$ : $\hat{a}|n\rangle=k|n-1\rangle$.
Prenons la norme de cet état : $|a|n\rangle|^2 = \langle n|\hat{a}^\dagger\hat{a}|n\rangle=|k|^2\langle n-1|n-1\rangle=|k|^2$ (vu que les états propres de l’oscillateur harmonique sont normalisés).
Mais on peut remarquer aussi que $\langle n|\hat{a}^\dagger\hat{a}|n\rangle=\langle n|\hat{n}|n\rangle =n$.
On obtient par conséquent $k=\sqrt{n}$ (cela suppose $k$ réel mais comme les états sont définis à une phase près, on peut toujours choisir la phase afin que $k$ soit bien réel).
On a aussi montré que $\hat{a}^\dagger=c|n+1\rangle$ et $|a^\dagger|n\rangle|^2 = \langle n|\hat{a}\hat{a}^\dagger|n\rangle=|c|^2\langle n+1|n+1\rangle=|c|^2$.
Et comme $\hat{a}\hat{a}^\dagger=1+\hat{n}$, $\langle n|\hat{a}\hat{a}^\dagger|n\rangle=\langle n|1+\hat{n}|n\rangle=n+1$.
Et donc $c=\sqrt{n+1}$
On vérifie bien que $\hat{a}|0\rangle=0$. $|0\rangle$ est effectivement l’état fondamental de l’oscillateur harmonique, on ne peut pas aller plus bas.
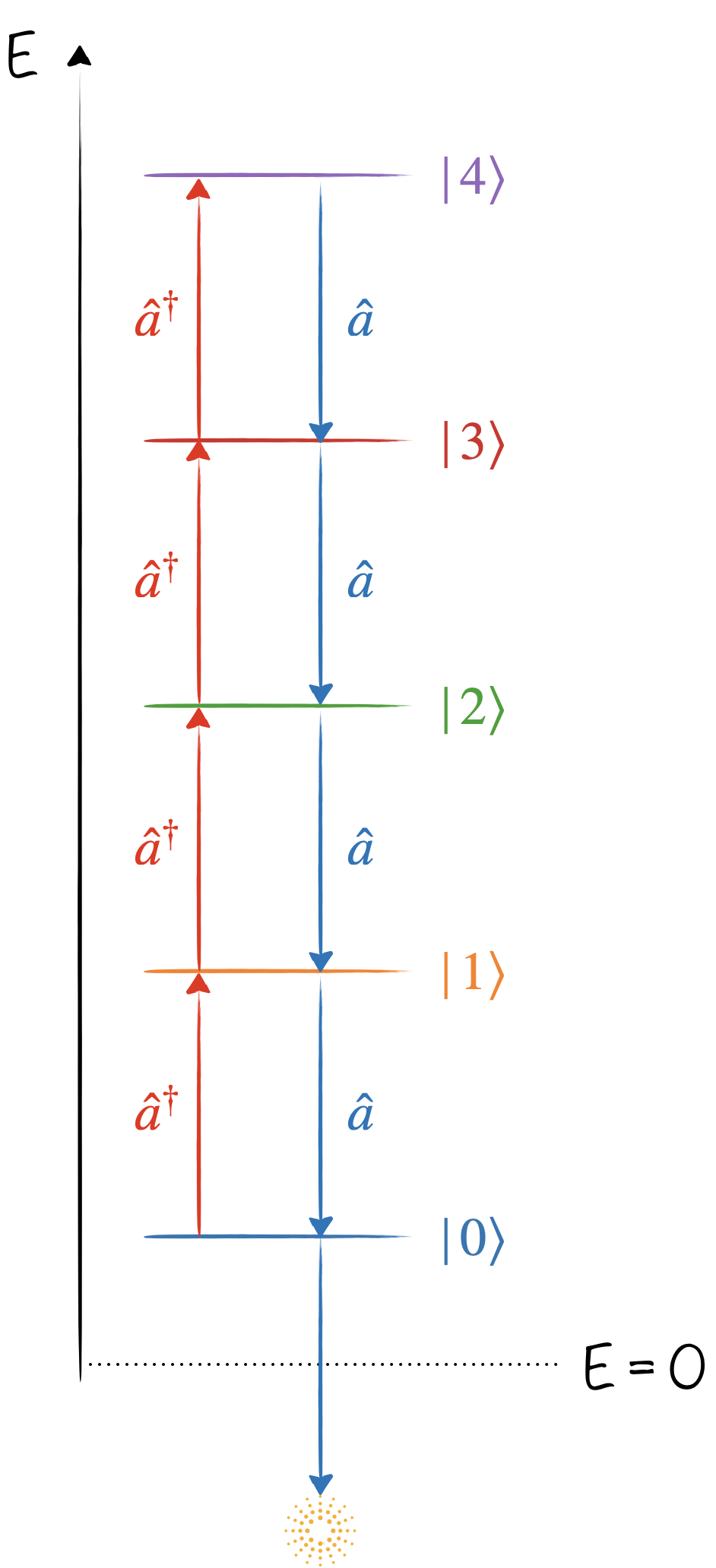
Et on retrouve aussi l’énergie de point zéro $E_0=\frac{1}{2}\hbar\omega$ :
$$\displaystyle\hat{H}|0\rangle=\hbar\omega\left(\hat{n}+\frac{1}{2}\right)|0\rangle=\frac{1}{2}\hbar\omega|0\rangle$$
Montons maintenant les barreaux de l’échelle en créant à chaque fois ce qui a tout l’air d’une particule d’énergie $\hbar\omega$ :
$\displaystyle\hat{a}^\dagger|0\rangle=|1\rangle$,
$\displaystyle\hat{a}^\dagger|1\rangle=\sqrt{2}|2\rangle \rightarrow |2\rangle=\frac{(\hat{a}^\dagger)^2}{\sqrt{2}}|0\rangle$,
$\displaystyle\hat{a}^\dagger|2\rangle=\sqrt{3}|3\rangle \rightarrow |3\rangle=\frac{(\hat{a}^\dagger)^3}{\sqrt{3\times 2}}|0\rangle$…
Et en généralisant, $\displaystyle |n\rangle=\frac{(\hat{a}^\dagger)^n}{\sqrt{n!}}|0\rangle$.
Le problème ondulatoire de départ a spontanément produit des particules !
Supposons maintenant qu’on ait affaire à un troupeau de $N$ oscillateurs harmoniques indépendants, sans couplage. L’Hamiltonien devient $\displaystyle \hat{H}=\sum_{k=1}^N\hat{H}_k$ qu’on peut réécrire :
$$\displaystyle \hat{H}=\sum_{k=1}^N\hbar\omega_k\left(\hat{a}^\dagger_k\hat{a}^{\phantom{\dagger}}_k+\frac{1}{2}\right)$$
Un état général du système est donné par $|n_1,n_2,\cdots,n_N\rangle$. C’est la représentation en nombre d’occupation. Et on a :
$$|{n_k}\rangle=\prod_k\frac{1}{\sqrt{n_k !}}(\hat{a}^\dagger_k)^{n_k}|0\rangle$$
Couplons maintenant tous ces petits ressorts.

L’Hamiltonien qui tient compte de l’interaction entre les oscillateurs s’écrit :
$$\hat{H}=\sum_j\frac{\hat{p}_j^2}{2m}+\frac{1}{2}K(\hat{x}_{j+1}-\hat{x}_j)^2$$
Les excitations de ce système se comportent exactement comme un jeu d’oscillateurs indépendants. Par quel miracle ? La transformée de Fourier permet de diagonaliser l’Hamiltonien. En effet, si les masses sont bien couplées dans l’espace réel, les excitations se découplent dans l’espace réciproque.
En supposant que les oscillateurs sont séparés d’une distance $a$, les transformées de Fourier de $x_j$ et $p_j$ s’écrivent :
En substituant dans l’Hamiltonien, on obtient :
$$\hat{H}=\sum_k\left[\frac{1}{2m}\hat{p}_k\hat{p}_{-k}+\frac{1}{2}m\omega_k^2\hat{x}_k\hat{x}_{-k}\right]$$
où on a laissé tomber les tildes et où $\omega_k^2=(4K/m)\sin^2(ka/2)$.
Astuce pour gérer des expressions du type :
$$ \frac{1}{N} \sum_j \sum_{k q} \tilde{p}_k \tilde{p}_q \mathrm{e}^{\mathrm{i}(k+q) j a} $$
L’idée est de commencer par la somme spatiale en utilisant l’identité $\sum_j \mathrm{e}^{\mathrm{i}\left(k-k^{\prime}\right) j a}=N \delta_{k k^{\prime}}$. Cela donne :
$$ \sum_{k q} \tilde{p}_k \tilde{p}_q \delta_{k,-q} $$
Puis on utilise le Kronecker sur la somme des moments. Cela fixe $q=-k$, nous laissant avec une somme sur un seul indice :
$$ \sum_k \tilde{p}_k \tilde{p}_{-k} $$
Chaque mode de Fourier $k$ se comporte donc comme un oscillateur harmonique indépendant.
On peut à nouveau introduire des opérateurs de création et d’annihilation :
$$ \hat{a}_k = \sqrt{\frac{m\omega_k}{2\hbar}}\left(\hat{x}_k+\frac{\mathrm{i}}{m\omega_k}\hat{p}_k\right)\qquad\displaystyle \hat{a}^\dagger_k = \sqrt{\frac{m\omega_k}{2\hbar}}\left(\hat{x}_{-k}-\frac{\mathrm{i}}{m\omega_k}\hat{p}_{-k}\right) $$
À partir d’eux, on peut isoler $\hat{x}_k$ et $\hat{p}_k$ :
$$ \hat{x}_k=\sqrt{\frac{\hbar}{2 m \omega_k}}\left(\hat{a}_k+\hat{a}_{-k}^{\dagger}\right) \qquad \hat{p}_k= -\mathrm{i} \sqrt{\frac{m \hbar \omega_k}{2}}\left(\hat{a}_k-\hat{a}_{-k}^{\dagger}\right) $$
En réinjectant dans l’Hamiltonien, on obtient finalement, après réindexation et utilisation de la relation de commutation $\left[\hat{a}_k, \hat{a}_{k^{\prime}}^{\dagger}\right]=\delta_{k, k^{\prime}}$ :
$$\hat{H}=\sum_{k=1}^N\hbar\omega_k\left(\hat{a}_k^\dagger\hat{a}^{\phantom{\dagger}}_k+\frac{1}{2}\right)$$
On appelle ces modes étiquetés par le vecteur d’onde $k$ des phonons. Et chacun de ces phonons peut porter des multiples entiers du quantum d’énergie $\hbar\omega_k$.
Les paquets d’énergie que peut accepter le phonon ressemblent à des particules. Pourquoi alors ne pas considérer les phonons eux-mêmes comme des particules ?
C’est le cœur de la seconde quantification : un problème ondulatoire peut s’exprimer comme une collection d’oscillateurs et produit donc des particules.
Représentation en nombre d’occupation
On va se débarrasser des fonctions d’ondes, en passant de la représentation $(x,p)$ à un nouveau type de représentation.
On place une particule dans une boite de taille $L$ (on prend dans la suite $\hbar=1$).
L’opérateur impulsion $\hat{p}$ pour un mouvement dans la direction $x$ est $\hat{p}=-\mathrm{i}\frac{\partial}{\partial x}$. Les solutions de l’équation de Schrödinger pour la particule dans la boite sont les états propres de l’opérateur impulsion, les ondes planes $\psi(x)=\frac{1}{\sqrt{L}}\mathrm{e}^{\mathrm{i}px}$. Utiliser des conditions aux limites périodiques ($\psi(x+L)=\psi(x)$) entraîne que $\mathrm{e}^{\mathrm{i}p(x+L)}={\mathrm{e}}^{\mathrm{i}px}$ et implique donc que $\mathrm{e}^{\mathrm{i}pL}=1$. Satisfaire la condition nécessite que $pL=2\pi m$ avec $m$ entier. Cela impose donc une quantification des états d’impulsion que peut prendre la particule dans la boite :
$$p_m = \frac{2\pi m}{L}$$
Si on a plusieurs particules sans interaction dans la boite, l’énergie totale est donnée par $\sum_m n_{p_m}E_{p_m}$ où $n_{p_m}$ est le nombre de particules dans l’état $|p_m\rangle$.
Plutôt que de noter un état à plusieurs particules identiques de cette façon $|p_1 p_2 p_1 p_3 p_5\rangle$ (ici pour 5 particules), on va juste lister le nombre de particules dans chacun des états, ce qui donne pour l’exemple précédent $|21101\rangle$. On dit qu’on passe alors à une représentation en nombre d’occupation qu’on a déjà rencontrée dans le chapitre précédent.
Agir avec l’Hamiltonien sur un état dans la représentation en nombre d’occupation permet d’obtenir l’énergie vue un peu plus haut :
Dans le cas d’une collection d’oscillateurs harmoniques, on a vu dans le chapitre précédent qu’on peut se débarrasser de quasiment tous les vecteurs d’état (excepté le vide $|0\rangle$) grâce à l’opérateur de création :
$$|n_1 n_2\ldots\rangle = \prod_k\frac{1}{(n_k !)^{\frac{1}{2}}}(\hat{a}_k^\dagger)^{n_k}|0\rangle$$
On crée ainsi un état général de plusieurs oscillateurs harmoniques en agissant sur l’état du vide. Mais on veut aller plus loin qu’une une création de quanta dans des oscillateurs… L’ambition est une création de particules dans des états d’impulsion donnés. On veut un opérateur de création $\hat{a}^\dagger_{p_m}$ pour faire naître une particule dans l’état d’impulsion $|p_m\rangle$. Peut-on juste changer $k$ en $p_m$ pour passer de la création d’un quantum dans l’oscillateur $k$ à une particule dans l’état d’impulsion $|p_m\rangle$ ? Presque… Juste une petite question de symétrie à régler.
Considérons par exemple un système à deux états d’impulsion $p_1$ et $p_2$ décrits dans la représentation en nombre d’occupation $|n_1n_2\rangle$. Chacun de ses états est formé en agissant sur l’état du vide $|0\rangle$. Définissons $\hat{a}_{p_1}^\dagger|0\rangle=|10\rangle$ et $\hat{a}_{p_2}^\dagger|0\rangle=|01\rangle$ et ajoutons une nouvelle particule dans l’état inoccupé : $\hat{a}_{p_2}^\dagger\hat{a}_{p_1}^\dagger|0\rangle\propto|11\rangle$, $\hat{a}_{p_1}^\dagger\hat{a}_{p_2}^\dagger|0\rangle\propto|11\rangle$ où la constante de proportionnalité reste à déterminer.
Suivant qu’on ajoute une particule dans l’état $p_1$ puis une autre dans l’état $p_2$ ou dans l’ordre inverse, on doit finir avec le même état $|11\rangle$, ce qui implique $\hat{a}_{p_1}^\dagger\hat{a}_{p_2}^\dagger = \lambda\hat{a}_{p_2}^\dagger\hat{a}_{p_1}^\dagger$ où $\lambda$ est une constante.
Deux possibilités évidentes pour $\lambda$ : $\lambda=\pm 1$. Elles correspondent à des fonctions d’onde qui sont soit symétriques, soit antisymétriques lors de l’échange des deux particules. Les particules sont appelées bosons dans le cas symétrique et fermions dans le cas antisymétrique. Ces deux cas correspondent à deux relations de commutation possibles entre les opérateurs de création et d’annihilation.
Cas 1 : $\lambda=1$, les bosons
On a dans ce cas $\hat{a}_{p_1}^\dagger\hat{a}_{p_2}^\dagger = \hat{a}_{p_2}^\dagger\hat{a}_{p_1}^\dagger$ et donc (en étiquetant les opérateurs de manière plus générale),
$$\left[\hat{a}_i^\dagger,\hat{a}_j^\dagger\right]=0$$
Les opérateurs de création pour différents états de particule commutent.
On a aussi $\left[\hat{a}_i,\hat{a}_j\right]=0$ et on définit $\left[\hat{a}_i,\hat{a}_j^\dagger\right]=\delta_{ij}$.
On obtient donc un formalisme identique à celui des oscillateurs harmoniques et on peut alors construire un état général à plusieurs particules sur le même modèle :
$$|n_1n_2\cdots\rangle=\prod_m\frac{1}{(n_{p_m}!)^{\frac{1}{2}}}(\hat{a}^\dagger_{p_m})^{n_{p_m}}|0\rangle$$
Les particules ainsi décrites sont des bosons.
Trois propriétés saillantes :
- On peut placer tout nombre de particules dans chaque état quantique (on peut les empiler dans un même état d’impulsion).
- Ces états sont symétriques lors de l’échange de deux particules.
- Enfin, l’ordre d’ajout des particules ne modifie pas l’état final obtenu : $\hat{a}^\dagger_{p_1}\hat{a}^\dagger_{p_2}|0\rangle=\hat{a}^\dagger_{p_2}\hat{a}^\dagger_{p_1}|0\rangle=|1_{p_1}1_{p_2}\rangle$.
Action des opérateurs sur un état général :
$$ \begin{aligned} &\hat{a}_i^\dagger |n_1\cdots n_i\cdots\rangle = \sqrt{n_i+1}|n_1\cdots n_i+1\cdots\rangle\\ &\hat{a}_i |n_1\cdots n_i\cdots\rangle = \sqrt{n_i}|n_1\cdots n_i-1\cdots\rangle \end{aligned} $$
Cas 2 : $\lambda=-1$, les fermions
On va noter les opérateurs des fermions $\hat{c}_i^\dagger$ pour les différentier de ceux des bosons.
On obtient $\left\{\hat{c}_i^\dagger,\hat{c}_j^\dagger\right\} \equiv \hat{c}_i^\dagger \hat{c}_j^\dagger + \hat{c}_j^\dagger\hat{c}_i^\dagger = 0$ où on a défini l’anticommutateur de deux opérateurs.
Les opérateurs des fermions anticommutent : $\hat{c}_i^\dagger\hat{c}_j^\dagger+\hat{c}_j^\dagger\hat{c}_i^\dagger=0$.
En prenant $i=j$, on obtient $\hat{c}_i^\dagger\hat{c}_i^\dagger+\hat{c}_i^\dagger\hat{c}_i^\dagger=0\Rightarrow \hat{c}_i^\dagger\hat{c}_i^\dagger=0$. Essayer de caser deux particules dans le même état d’impulsion aboutit à leur annihilation complète.
C’est le principe de Pauli ; chaque état quantique ne peut être occupé que par un et un seul fermion !
On a aussi $\left\{\hat{c}_i,\hat{c}_j\right\}=0$ et on définit $\left\{\hat{c}_i,\hat{c}_j^\dagger\right\}=\delta_{ij}$ pour pouvoir appliquer ici aussi l’analogie avec les oscillateurs harmoniques. Mais gare maintenant à l’ordre des opérateurs qui n’est plus indifférent !
Action des opérateurs sur un état général :
$$ \begin{aligned} &\hat{c}_i^\dagger |n_1\cdots n_i\cdots\rangle = (-1)^{\sum_i}\sqrt{1-n_i}|n_1\cdots n_i+1\cdots\rangle\\ &\hat{c}_i |n_1\cdots n_i\cdots\rangle = (-1)^{\sum_i}\sqrt{n_i}|n_1\cdots n_i-1\cdots\rangle \end{aligned} $$
Où $(-1)^{\sum_i}=(-1)^{n_1+n_2+\cdots+n_{i-1}}$. Cela donne un facteur $(-1)$ pour chaque particule placée à gauche de l’état étiqueté par $n_i$ dans le vecteur d’état.
Prenons un exemple pour s'aguerrir et vérifier la formule.
Pour échanger de place de particules, on va leur faire suivre le processus suivant $|110\rangle\rightarrow|101\rangle\rightarrow|011\rangle\rightarrow|110\rangle$.
Bouger une particule de place consiste à détruire la particule à un endroit et à la créer à un autre.
Déplacer une particule de l’état 2 vers l’état 3 s’écrit donc $\hat{a}^\dagger_{3}\hat{a}_2|110\rangle$. L’enchaînement total proposé peut être décrit par l’enchaînement $\hat{a}^\dagger_{1}\hat{a}_3\hat{a}^\dagger_{2}\hat{a}_1\hat{a}^\dagger_{3}\hat{a}_2|110\rangle$. Et le résultat est sensé être $\pm|110\rangle$ ($+$ pour des bosons et $-$ pour des fermions).
Vérifions que les relations de commutation donnent les bons résultats. S’il s’agit de bosons, on peut échanger de place deux opérateurs agissant sur des états différents ($[\hat{a}_i,\hat{a}_j]=0$).
$\hat{a}^\dagger_{1}\hat{a}_3\hat{a}^\dagger_{2}\hat{a}_1\hat{a}^\dagger_{3}\hat{a}_2|110\rangle=\hat{a}_3\hat{a}^\dagger_{3}\hat{a}^\dagger_{1}\hat{a}_1\hat{a}^\dagger_{2}\hat{a}_2|110\rangle$
Comme $\hat{a}^\dagger_i\hat{a}_i=\hat{n}_i$, l’opérateur nombre qui compte le nombre de particules dans l’état $i$, on obtient :
$\hat{a}_3\hat{a}^\dagger_{3}\hat{a}^\dagger_{1}\hat{a}_1\hat{a}^\dagger_{2}\hat{a}_2|110\rangle=\hat{a}_3\hat{a}^\dagger_{3}\hat{n}_1\hat{n}_2|110\rangle =(1)\times(1)\times \hat{a}_3\hat{a}^\dagger_{3}|110\rangle$
En utilisant $[\hat{a}_3,\hat{a}^\dagger_3]=1$, on obtient :
$\hat{a}_3\hat{a}^\dagger_{3}|110\rangle=(1+\hat{n}_3)|110\rangle = |110\rangle + 0 =|110\rangle$
Passons aux fermions. L’échange entre deux particules s’accompagne maintenant d’un changement de signe.
$\hat{c}^\dagger_{1}\hat{c}_3\hat{c}^\dagger_{2}\hat{c}_1\hat{c}^\dagger_{3}\hat{c}_2|110\rangle = -\hat{c}_3\hat{c}^\dagger_{3}\hat{c}^\dagger_{1}\hat{c}_1\hat{c}^\dagger_{2}\hat{c}_2|110\rangle$ car on compte un nombre impair d’échanges. Et $-\hat{c}_3\hat{c}^\dagger_{3}\hat{c}^\dagger_{1}\hat{c}_1\hat{c}^\dagger_{2}\hat{c}_2|110\rangle = -(1-\hat{n}_3)|110\rangle = -|110\rangle$. Youpi !
On était jusque-là confiné dans une boite, mais que se passe-t-il si on écarte ses murs infiniment ? On passe alors à la limite du continu. Le symbole de Kronecker $\delta_{ij}$ des commutateurs devient une fonction delta de Dirac $\delta^{(3)}(\boldsymbol{p})$ et les sommes discrètes deviennent des intégrales.
Le commutateur se transforme donc en :
$$\left[\hat{a}_\boldsymbol{p},\hat{a}^\dagger_\boldsymbol{q}\right]=\delta^{(3)}(\boldsymbol{p}-\boldsymbol{q})$$
et l’Hamiltonien :
$$\hat{H}=\int\mathrm{d}^3 p\, E_\boldsymbol{p}\hat{a}^\dagger_\boldsymbol{p}\hat{a}_\boldsymbol{p}$$
Pour montrer que cette nouvelle formulation est correcte, on va retrouver à partir d’elle les bonnes fonctions d’onde dans l’espace des positions.
Pour des états à une seule particule, on a :
$$\langle \boldsymbol{p}|\boldsymbol{p’}\rangle=\langle 0|\hat{a}_\boldsymbol{p}\hat{a}^\dagger_\boldsymbol{p’}|0\rangle$$
Et avec les relations de commutation, on obtient :
$$\langle \boldsymbol{p}|\boldsymbol{p’}\rangle=\langle 0|\left[\delta^{(3)}(\boldsymbol{p}-\boldsymbol{p’})\pm \hat{a}^\dagger_\boldsymbol{p’}\hat{a}_\boldsymbol{p} \right]|0\rangle=\delta^{(3)}(\boldsymbol{p}-\boldsymbol{p’})$$
Vérifions que c’est la relation attendue en passant en représentation position.
Par un changement de base, $|\boldsymbol{x}\rangle = \int\mathrm{d}q\,\phi^*_\boldsymbol{q}(\boldsymbol{x})|\boldsymbol{q}\rangle$
changement de base
L’état $|\boldsymbol{x}\rangle$ peut s’écrire dans une nouvelle base en utilisant la relation de fermeture $1=\int\mathrm{d}^3q\,|\boldsymbol{q}\rangle\langle\boldsymbol{q}|$ de telle sorte que $|\boldsymbol{x}\rangle = \int\mathrm{d}^3q\,|\boldsymbol{q}\rangle\langle\boldsymbol{q}|\boldsymbol{x}\rangle$. Et comme $\langle\boldsymbol{x}|\boldsymbol{q}\rangle=\phi_\boldsymbol{q}(\boldsymbol{x})$ et $\langle\boldsymbol{q}|\boldsymbol{x}\rangle=\phi^*_\boldsymbol{q}(\boldsymbol{x})$, on obtient bien $|\boldsymbol{x}\rangle = \int\mathrm{d}q\,\phi^*_\boldsymbol{q}(\boldsymbol{x})|\boldsymbol{q}\rangle$.
Cela donne $\langle \boldsymbol{x}|\boldsymbol{p}\rangle = \int\mathrm{d}^3q\,\phi_\boldsymbol{q}(\boldsymbol{x})\langle\boldsymbol{q}|\boldsymbol{p}\rangle=\phi_\boldsymbol{p}(\boldsymbol{x})$.
C’est bien ce qui était attendu, mais rien de bien folichon.
Passons maintenant au cas d’un état à deux particules : $\langle \boldsymbol{p’}\boldsymbol{q’}|\boldsymbol{q}\boldsymbol{p}\rangle=\langle 0|\hat{a}_\boldsymbol{p’}\hat{a}_\boldsymbol{q’}\hat{a}^\dagger_\boldsymbol{q}\hat{a}^\dagger_\boldsymbol{p}|0\rangle$.
Par utilisation des relations de commutation, on arrive à $\langle \boldsymbol{p’}\boldsymbol{q’}|\boldsymbol{q}\boldsymbol{p}\rangle=\delta^{(3)}(\boldsymbol{p’}-\boldsymbol{p})\delta^{(3)}(\boldsymbol{q’}-\boldsymbol{q})\pm\delta^{(3)}(\boldsymbol{p’}-\boldsymbol{q})\delta^{(3)}(\boldsymbol{q’}-\boldsymbol{p})$ avec le signe plus pour les bosons et moins pour les fermions.
Déterminons à nouveau la fonction d’onde dans l’espace des positions grâce au changement de base :
$$|\boldsymbol{x}\boldsymbol{y}\rangle = \frac{1}{\sqrt{2!}}\int \mathrm{d}^3p’\mathrm{d}^3 q’ \phi^*_\boldsymbol{p’}(\boldsymbol{x})\phi^*_\boldsymbol{q’}(\boldsymbol{y})|\boldsymbol{p’}\boldsymbol{q’}\rangle$$
où le facteur $\frac{1}{\sqrt{2!}}$ compense le double comptage $q’p’$/$p’q’$ dû au fait que la somme n’est pas restreinte. Cela donne :
$$ \frac{1}{\sqrt{2!}}\int \mathrm{d}^3p’\mathrm{d}^3 q’ \phi_\boldsymbol{p’}(\boldsymbol{x})\phi_\boldsymbol{q’}(\boldsymbol{y}) \langle \boldsymbol{p’}\boldsymbol{q’}|\boldsymbol{p}\boldsymbol{q}\rangle = \frac{1}{\sqrt{2!}}[\phi_\boldsymbol{p}(\boldsymbol{x})\phi_\boldsymbol{q}(\boldsymbol{y})\pm \phi_\boldsymbol{q}(\boldsymbol{x})\phi_\boldsymbol{p}(\boldsymbol{y})]$$
On retrouve l’expression d’un état à deux particules !
Cette nouvelle formulation de la mécanique quantique semble donc valide et dans la suite, elle va porter ses fruits.
Seconde quantification
On considère à nouveau ici des particules non relativistes dans une boîte. Cela simplifie pas mal mais cela permet déjà d’étudier le comportement d’électrons dans un solide.
Particule dans une boîte de volume $\mathcal{V}$
Un état $|\alpha\rangle$ se décrit en représentation position $\psi_\alpha(\boldsymbol{x})=\langle\boldsymbol{x}|\alpha\rangle$ et en représentation impulsion $\tilde{\psi}_\alpha(\boldsymbol{p})=\langle\boldsymbol{p}|\alpha\rangle$ et comme $\langle\boldsymbol{p}|\alpha\rangle:\int\mathrm{d}^3\langle\boldsymbol{p}|\boldsymbol{x}\rangle\langle\boldsymbol{x}|\alpha\rangle$, on déduit $\langle\boldsymbol{p}|\boldsymbol{x}\rangle=\frac{1}{\sqrt{\mathcal{V}}}\mathrm{e}^{-\mathrm{i}\boldsymbol{p}\cdot\boldsymbol{x}}$ (par identification avec la transformée de Fourier $\tilde{\psi}_\alpha(\boldsymbol{p})=\frac{1}{\sqrt{\mathcal{V}}}\int\mathrm{d}^3 x\,\mathrm{e}^{-\mathrm{i}\boldsymbol{p}\cdot\boldsymbol{x}}\psi_\alpha(\boldsymbol{x})$).
La transformée de Fourier inverse est discrète puisque les valeurs de $\boldsymbol{p}$ le sont : $\psi_\alpha(\boldsymbol{x})=\frac{1}{\sqrt{\mathcal{V}}}\sum_\boldsymbol{p}\mathrm{e}^{\mathrm{i}\boldsymbol{p}\cdot\boldsymbol{x}}\tilde{\psi}_\alpha(\boldsymbol{p})$.
Et on a aussi $\int\mathrm{d}^3 x\,\mathrm{e}^{-\mathrm{i}\boldsymbol{p}\cdot\boldsymbol{x}} = \mathcal{V}\delta_{\boldsymbol{p},0}$ et $\frac{1}{\mathcal{V}}\sum_\boldsymbol{p}\mathrm{e}^{\mathrm{i}\boldsymbol{p}\cdot\boldsymbol{x}}=\delta^{(3)}(\boldsymbol{x})$.
On sait d’ores et déjà créer une particule d’impulsion $\boldsymbol{p}$ à partir de l’état du vide en appliquant l’opérateur de création : $\hat{a}^\dagger_\boldsymbol{p}|0\rangle$. On obtient ainsi une particule complètement localisée dans l’espace des impulsions et donc s’étendant sur tout l’espace des coordonnées. Supposons maintenant que l’on veuille créer une particule localisée dans l’espace des coordonnées. Dans ce but, on construit des nouveaux opérateurs de création et d’annihilation appelés opérateur de champ par transformée de Fourier discrète des opérateurs $\hat{a}^\dagger_\boldsymbol{p}$ et $\hat{a}_\boldsymbol{p}$.
$$\hat{\psi}^\dagger(\boldsymbol{x}) = \frac{1}{\sqrt{\mathcal{V}}}\sum_\boldsymbol{p}\hat{a}^\dagger_\boldsymbol{p}\mathrm{e}^{-\mathrm{i}\boldsymbol{p}\cdot\boldsymbol{x}}$$
$$\hat{\psi}(\boldsymbol{x}) = \frac{1}{\sqrt{\mathcal{V}}}\sum_\boldsymbol{p}\hat{a}_\boldsymbol{p}\mathrm{e}^{\mathrm{i}\boldsymbol{p}\cdot\boldsymbol{x}}$$
Ces opérateurs de champ peuvent créer et annihiler une particule en une position $\boldsymbol{x}$.
Pour s’en convaincre, explorons l’état $|\Psi\rangle = \hat{\psi}^\dagger(\boldsymbol{x})|0\rangle$. On a d’une part $\sum_\boldsymbol{q}\hat{n}_\boldsymbol{q}|\Psi\rangle = |\Psi\rangle$, ce qui signifie que $|\Psi\rangle$ est un état propre de l’opérateur nombre d’occupation pour la valeur propre 1 et donc qu’une seule particule a été créée. D’autre part $\langle\boldsymbol{y}|\Psi\rangle=\delta^{(3)}(\boldsymbol{x}-\boldsymbol{y})$, ce qui prouve que la particule créée est bien localisée en $\boldsymbol{x}$.
$$ \begin{aligned} \langle\boldsymbol{y}|\Psi\rangle = \langle\boldsymbol{y}|\psi^\dagger(\boldsymbol{x})|0\rangle &= \frac{1}{\sqrt{\mathcal{V}}}\sum_\boldsymbol{p}\mathrm{e}^{-\mathrm{i}\boldsymbol{p}\cdot\boldsymbol{x}}\langle\boldsymbol{y}|\boldsymbol{p}\rangle\\ &=\frac{1}{\sqrt{\mathcal{V}}}\sum_\boldsymbol{p}\mathrm{e}^{-\mathrm{i}\boldsymbol{p}\cdot(\boldsymbol{x}-\boldsymbol{y})}\\ &=\delta^{(3)}(\boldsymbol{x}-\boldsymbol{y}) \end{aligned} $$
Les opérateurs de champ satisfont les relations de commutation suivantes :
-
pour des bosons : $\left[\hat{\psi}(\boldsymbol{x}),\hat{\psi}^\dagger(\boldsymbol{y})\right]=\delta^{(3)}(\boldsymbol{x}-\boldsymbol{y})$, $\left[\hat{\psi}^\dagger(\boldsymbol{x}),\hat{\psi}^\dagger(\boldsymbol{y})\right]=0$ et $\left[\hat{\psi}(\boldsymbol{x}),\hat{\psi}(\boldsymbol{y})\right]=0$
-
et pour des fermions : $\left\{\hat{\psi}(\boldsymbol{x}),\hat{\psi}^\dagger(\boldsymbol{y})\right\}=\delta^{(3)}(\boldsymbol{x}-\boldsymbol{y})$, $\left\{\hat{\psi}^\dagger(\boldsymbol{x}),\hat{\psi}^\dagger(\boldsymbol{y})\right\}=0$ et $\left\{\hat{\psi}(\boldsymbol{x}),\hat{\psi}(\boldsymbol{y})\right\}=0$
C’est le moment : on va maintenant apprendre à upgrader les opérateurs issus de la première quantification en opérateurs de seconde quantification !
Rappelons-nous d’abord qu’un opérateur $\hat{\mathcal{A}}$ associe à l’état quantique $|\psi\rangle$, élément de l’espace de Hilbert, un nouvel état quantique $\hat{\mathcal{A}}|\psi\rangle$.
On va supposer ici que $\hat{\mathcal{A}}$ n’agit que sur une seule particule à la fois (contrairement à un opérateur potentiel d’interaction par exemple). En utilisant doublement la relation de fermeture et en partant de l’égalité triviale $\hat{\mathcal{A}}=\hat{\mathcal{A}}$, on peut obtenir la décomposition de $\hat{\mathcal{A}}$ sur une base donnée de l’espace de Hilbert :
$$\hat{\mathcal{A}}=\sum_{\alpha,\beta}|\alpha\rangle\langle\alpha|\hat{\mathcal{A}}|\beta\rangle\langle\beta|=\sum_{\alpha,\beta}\mathcal{A}_{\alpha\beta}|\alpha\rangle\langle\beta|$$
où les $\mathcal{A}_{\alpha\beta}=\langle\alpha|\hat{\mathcal{A}}|\beta\rangle$ sont les éléments de matrice de la décomposition de l’opérateur, ils donnent l’amplitude de la transition d’un état $|\beta\rangle$ vers un état $|\alpha\rangle$.
L’idée va être de passer de cette transition entre états à un transfert de particules (mort de l’une suivie de la naissance d’une autre).
L’espace de Hilbert permet de décrire l’état d’une particule. L’espace de Fock rend possible, lui, la description d’états à $N$ particules (l’espace de Fock $\mathcal{F}$ inclut tous les états à $N$-particules pour toutes les valeurs de $N$ : $\mathcal{F}=\bigoplus_{N=0}^\infty \mathcal{F}_N=\mathcal{F}_0\oplus\mathcal{F}_1\oplus\cdots$ où $\mathcal{F}_0=\{|0\rangle\}$ est un ensemble ne contenant que l’état du vide et $\mathcal{F}_1$ est l’espace de Hilbert. Les sous-espaces $\mathcal{F}_{N≥2}$ doivent être symétrisés pour des bosons et antisymétrisés pour des fermions (donc $\mathcal{F}_2$ n’est pas seulement $\mathcal{F}_1\otimes\mathcal{F}_1$ mais seulement sa partie symétrique ou antisymétrique). Les opérateurs de création permettent de passer d’un élément de $\mathcal{F}_N$ à un élément de $\mathcal{F}_{N+1}$ et les opérateurs d’annihilation font l’inverse.
La version seconde quantification $\hat{A}$ de l’opérateur $\hat{\mathcal{A}}$ qui correspond à l’upgrade d’un opérateur à une particule agissant sur l’espace de Hilbert vers un opérateur multi-particules agissant sur l’espace de Fock est simplement donnée par :
$$\hat{A} = \sum_{\alpha\beta}\mathcal{A}_{\alpha\beta}\hat{a}^\dagger_\alpha\hat{a}_\beta$$
Les éléments de matrice $\mathcal{A}_{\alpha\beta}$ sont les mêmes qu’au-dessus et ils continuent à représenter l’ensemble des transitions possibles d’une particule seule. Mais $\hat{A}$ opère bien maintenant sur un état à plusieurs particules. On commence par utiliser $\hat{a}_\beta$ pour retirer une particule dans l’état $|\beta\rangle$, on multiplie par l’élément de matrice $\mathcal{A}_{\alpha\beta}$ donnant l’amplitude de la transition vers le nouvel état, et enfin on utilise $\hat{a}^\dagger_\alpha$ pour placer la particules dans l’état final $|\alpha\rangle$.
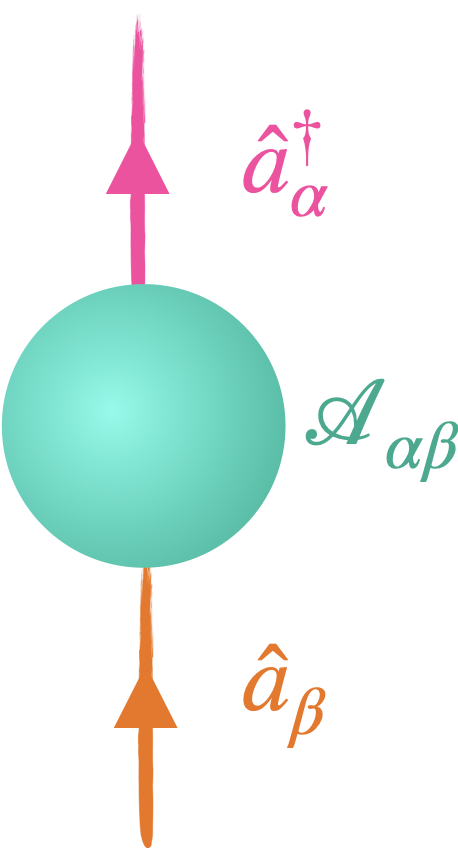
Dans les exemples suivants, on va construire pas à pas un Hamiltonien simple d’une particule unique soumise à un potentiel en version seconde quantification. L’idée est de se familiariser avec le formalisme et constater qu’il nous redonne bien les résultats qu’on attend.
La relation de fermeture $\hat{1}=\sum_\alpha|\alpha\rangle\langle\alpha|$ est l’exemple le plus simple de $\hat{\mathcal{A}} = \sum_{\alpha\beta}\mathcal{A}_{\alpha\beta}\hat{a}^\dagger_\alpha\hat{a}_\beta$ avec $\mathcal{A}_{\alpha\beta}=\delta_{\alpha\beta}$.
Sa promotion à l’étage de la seconde quantification est simplement $\hat{n}=\sum_\alpha\hat{a}^\dagger_\alpha\hat{a}_\alpha$, l’opérateur nombre qui compte un pour chaque particule dans l’état sur lequel il agit.
L’opérateur impulsion usuel peut s’écrire $\hat{\mathcal{A}}=\hat{\boldsymbol{p}}=\sum_\boldsymbol{p}\boldsymbol{p}|\boldsymbol{p}\rangle\langle\boldsymbol{p}|$ qui est promu automatiquement en $\hat{\boldsymbol{p}}=\sum_\boldsymbol{p}\boldsymbol{p}\,\hat{a}^\dagger_\boldsymbol{p}\hat{a}_\boldsymbol{p}=\sum_\boldsymbol{p}\boldsymbol{p}\,\hat{n}_\boldsymbol{p}$.
De même, une fonction de l’opérateur impulsion $\hat{\mathcal{A}}=f(\boldsymbol{p})$ devient $\hat{A}=\sum_\boldsymbol{p}f(\boldsymbol{p})\hat{a}^\dagger_\boldsymbol{p}\hat{a}_\boldsymbol{p}=\sum_\boldsymbol{p}f(\boldsymbol{p})\hat{n}_\boldsymbol{p}$.
Un exemple particulier d’une telle fonction : l’Hamiltonien d’une particule libre $\frac{\boldsymbol{p}^2}{2m}$.
L’Hamiltonien d’une particule libre devient ainsi en seconde quantification :
$\displaystyle\hat{H}=\sum_\boldsymbol{p}\frac{\boldsymbol{p}^2}{2m}\hat{n} _\boldsymbol{p}$
$\hat{H}$ est diagonal dans la base des états nombre d’occupation puisqu’ils sont des états propres de $\hat{n}_\boldsymbol{p}$. Et de fait, pour diagonaliser tout hamiltonien (ce qui revient à trouver les énergies des états propres), on n’a qu’à l’exprimer en termes de nombres d’opérateurs. Donc ici, on dit finalement que l’énergie totale du système est donnée par la somme des énergies $\frac{\boldsymbol{p}^2}{2m}$ de toutes les particules. Ça paraît sensé.
Et si l’opérateur est une fonction de $\hat{\boldsymbol{x}}$ plutôt que $\hat{\boldsymbol{p}}$ ?
La formule de promotion reste valable si les états $|\alpha\rangle$ et $|\beta\rangle$ sont des états de position. Il suffit de remplacer les opérateurs de création et d’annihilation par les opérateurs de champ, et la somme sur les impulsions par une intégrale sur l’espace.
On peut ainsi écrire l’opérateur $\hat{V}$ en version seconde-quantification :
$\displaystyle \hat{V}=\int\mathrm{d}^3 x\,\hat{\phi}^\dagger(\boldsymbol{x})V(\boldsymbol{x})\hat{\phi}(\boldsymbol{x})$
Et si on préfère repasser dans l’espace des impulsions :
$\displaystyle \hat{V}=\frac{1}{\mathcal{V}}\int\mathrm{d}^3 x\,\sum_{\boldsymbol{p}_1,\boldsymbol{p}_2} \hat{a}^\dagger_{\boldsymbol{p}_1}\mathrm{e}^{-\mathrm{i}\boldsymbol{p}_1\cdot\boldsymbol{x} }V(\hat{\boldsymbol{x}})\hat{a}_{\boldsymbol{p}_2}\mathrm{e}^{\mathrm{i}\boldsymbol{p}_2\cdot\boldsymbol{x} }$
En introduisant la transformée de Fourier de $V(\boldsymbol{x})$, $\tilde{V}_{\boldsymbol{p}}=\frac{1}{\mathcal{V}}\int\mathrm{d}^3 x\,V(\boldsymbol{x})\mathrm{e}^{-\mathrm{i}\boldsymbol{p}\cdot\boldsymbol{x} }$, la formule s’éclaircit :
$\displaystyle \hat{V}=\sum_{\boldsymbol{p}_1,\boldsymbol{p}_2}\tilde{V}_{\boldsymbol{p}_1-\boldsymbol{p}_2}\hat{a}^\dagger_{\boldsymbol{p}_1}\hat{a}_{\boldsymbol{p}_2}$
Schématisation du processus : une particule arrive avec l’impulsion $\boldsymbol{p}_2$, interagit avec un champ de potentiel (représenté par $\tilde{V}_{\boldsymbol{p}_1-\boldsymbol{p}_2}$) puis repart avec l’impulsion $\boldsymbol{p}_1$.
Rq : l’opérateur $\hat{V}$ n’est pas diagonal puisque les opérateurs $\hat{a}$ créent et annihilent des particules avec des impulsions différentes.
Étudions l’influence du potentiel sur les états et valeurs propres de l’Hamiltonien suivant :
$\displaystyle\hat{H} = E_0 \sum_{\boldsymbol{p}} \hat{d}_{\boldsymbol{p}}^\dagger \hat{d}_{\boldsymbol{p}} - \frac{V}{2} \sum_{\boldsymbol{p}_1 \boldsymbol{p}_2} \hat{d}_{\boldsymbol{p}_1}^\dagger \hat{d}_{\boldsymbol{p}_2}$
On limite le système à 3 niveaux d’énergie, ce qui permet d’exprimer les états dans une base $|n_{\boldsymbol{p}_1}n_{\boldsymbol{p}_2}n_{\boldsymbol{p}_3}\rangle$.
Commençons par débrancher le potentiel ($V=0$). Une particule placée dans ce système ne peut être que dans un des trois états suivants : $|100\rangle$, $|010\rangle$ ou $|001\rangle$.
Rebranchons le potentiel et voyons comment il agit sur chacun des trois états :
$\displaystyle\frac{V}{2} \sum_{\boldsymbol{p}_1 \boldsymbol{p}_2} \hat{d}_{\boldsymbol{p}_1}^\dagger \hat{d}_{\boldsymbol{p}_2} |100\rangle = \frac{V}{2} \sum_{\boldsymbol{p}_1 \boldsymbol{p}_2} \hat{d}_{\boldsymbol{p}_1}^\dagger \hat{d}_{\boldsymbol{p}_2} |010\rangle = \frac{V}{2} \sum_{\boldsymbol{p}_1 \boldsymbol{p}_2} \hat{d}_{\boldsymbol{p}_1}^\dagger \hat{d}_{\boldsymbol{p}_2} |001\rangle = \frac{V}{2} \left( |100\rangle + |010\rangle + |001\rangle \right)$
Une forme matricielle permet de synthétiser l’information :
$\displaystyle H = \left[E_0 \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} - \frac{V}{2} \begin{pmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{pmatrix}\right]$
Les valeurs propres de cette équation sont $\varepsilon=E_0,E_0,E_0-\frac{3V}{2}$. L’état fondamental du système $|\Omega\rangle$ a donc l’énergie $E_0-\frac{3V}{2}$ et l’état propre correspondant s’écrit $|\Omega\rangle = \frac{1}{\sqrt{3}} \left( |100\rangle + |010\rangle + |001\rangle \right)$.
L’état fondamental est donc une superposition 1:1:1 des trois états d’impulsion desquels on est parti.
Quel est l’équivalent de la densité de probabilité d’une fonction d’onde dans le langage de la seconde quantification ? La densité de particules en un point $\boldsymbol{x}$ !
L’opérateur densité $\hat{\rho}(\boldsymbol{x})$ est donné par : $$ \begin{aligned} \hat{\rho}(\boldsymbol{x}) &= \hat{\psi}^\dagger(\boldsymbol{x})\hat{\psi}(\boldsymbol{x})\\ &=\frac{1}{\mathcal{V}} \sum_{\boldsymbol{p}_1 \boldsymbol{p}_2} \mathrm{e}^{-\mathrm{i} (\boldsymbol{p}_1 - \boldsymbol{p}_2) \cdot \boldsymbol{x}} \hat{a}^\dagger_{\boldsymbol{p}_1} \hat{a}_{\boldsymbol{p}_2} \end{aligned} $$
On vérifie que le terme de densité de particule est adapté puisqu’en intégrant sur tout l’espace, on retrouve le nombre de particules : $\int \mathrm{d}^3x\hat{\rho}(\boldsymbol{x})= \sum_{\boldsymbol{p}_1 \boldsymbol{p}_2} \delta_{\boldsymbol{p}_2,\boldsymbol{p}_1} \hat{a}^\dagger_{\boldsymbol{p}_1} \hat{a}_{\boldsymbol{p}_2} = \sum_\boldsymbol{p} \hat{n}_\boldsymbol{p}$
Cet opérateur permet de réécrire l’opérateur énergie potentielle d’une particule unique soumise à un potentiel extérieur comme :
$\displaystyle \hat{V} = \int \mathrm{d}^3 x \, V(\boldsymbol{x}) \hat{\rho}(\boldsymbol{x})$.
Le cadre non-relativiste dans lequel on se place jusqu’ici est limité mais il permet déjà de jouer avec des modèles de matière condensée. Finissons donc le chapitre en appliquant notre nouveau formalisme à des électrons se déplaçant sur un réseau d’atomes.
Modèle des liaisons fortes pour l’énergie cinétique
Travaillons dans une base où $\hat{c}^\dagger_i$ crée un électron sur un site du réseau étiqueté $i$. Comme l’énergie cinétique d’une particule est d’autant plus grande que celle-ci est spatialement confinée (dans le cas d’un puits infini de largeur $L$, l’énergie cinétique vaut $E_n = \frac{1}{2m}\left( \frac{n\pi}{L}\right)^2$), on va considérer qu’un saut d’un site $j$ vers un site $i$ permet d’économiser l’énergie cinétique $t_{ij}$ (ce terme dépend d’une façon ou d’une autre du recouvrement entre les orbitales atomiques du réseau). L’Hamiltonien somme tous les sauts possibles :
$$\hat{H} = \sum_{ij}(-t_{ij})\hat{c}^\dagger_i\hat{c}_j$$
Chaque terme de la somme correspond à un processus où une particule est annihilée au site $j$ puis recréée au site $i$, modélisant un saut et sauvant ainsi l’énergie $t_{ij}$.

On va d’abord considérer le cas le plus simple où $t_{ij}=t$ pour des voisins immédiats et $t_{ij}=0$ sinon. L’Hamiltonien devient :
$$\hat{H} = -t\sum_{i\tau}\hat{c}^\dagger_i\hat{c}_{i+\tau}$$
où la somme sur $\tau$ se fait sur les plus proches voisins.
La combinaison bilinéaire $\hat{c}^\dagger_i\hat{c}_j$ rend l’Hamiltonien non diagonal. Pour le diagonaliser, on passe à nouveau en impulsion via les transformées de Fourier :
$$ \hat{H} = \sum_{\boldsymbol{k}} E_{\boldsymbol{k}}\hat{c}^\dagger_{\boldsymbol{k}} \hat{c}_{\boldsymbol{k}} $$
où la relation de dispersion est donnée par $E_{\boldsymbol{k}}=- \sum_{\tau} t \mathrm{e}^{\mathrm{i} \boldsymbol{k} \cdot \boldsymbol{r}_{\tau}}$.
Pour un réseau carré où $\tau$ parcourt les vecteurs $(a,0)$, $(-a,0)$, $(0,a)$ et $(0,-a)$, on obtient $E_{\boldsymbol{k}} = -2t \left( \cos(k_x a) + \cos(k_y a) \right)$

On a tracé ci-dessus les contours du profil énergétique dans l’espace réciproque (l’énergie est constante sur une ligne). Pour $t>0$, l’énergie est minimale au centre $(k_x,k_y)=(0,0)$, ce qui correspond à un électron délocalisé, occupant tout le réseau et donc sans mouvement.
Potentiel à deux particules
Ajoutons un deuxième électron capable d’interagir avec le premier.
Pour la promotion seconde quantification de $\mathcal{A}_{\alpha\beta\gamma\delta}=\langle\alpha,\beta|\hat{A}|\gamma,\delta\rangle$ on peut tenter intuitivement :
$$Â = \sum_{\alpha\beta\gamma\delta} A_{\alpha\beta\gamma\delta} \hat{a}^\dagger_\alpha \hat{a}^\dagger_\beta \hat{a}_\gamma \hat{a}_\delta$$
L’opérateurs à deux particules typique est le potentiel $\hat{V}$. Et il sera le plus souvent fonction des coordonnées spatiales. Son expression impliquant les opérateurs de champ est alors :
$$\hat{V} = \frac{1}{2} \int \mathrm{d}^3 x\, \mathrm{d}^3 y \, \hat{\psi}^\dagger(\boldsymbol{x}) \hat{\psi}^\dagger(\boldsymbol{y}) V(\boldsymbol{x}, \boldsymbol{y}) \hat{\psi}(\boldsymbol{y}) \hat{\psi}(\boldsymbol{x})$$
Le $\frac{1}{2}$ compense le double comptage des interactions. L’ordre des opérateurs n’est pas anodin ! Celui utilisé est appelé ordre normal et sa vertu principale est d’assurer que l’opérateur $\hat{V}$ ait une valeur moyenne prédite (espérance quantique) nulle pour l’état de vide ($\langle 0|\hat{V}|0\rangle=0$).
On restreint le potentiel à la forme $V(\boldsymbol{x}-\boldsymbol{y})$ ne dépendant que de la séparation relative des particules (cela va garantir la conservation de l’impulsion dans l’interaction) et on décompose en modes d’impulsion les opérateurs champ :
$$ \hat{V} = \frac{1}{2\mathcal{V}^2} \int \mathrm{d}^3x \,\mathrm{d}^3 y \!\!\sum_{\boldsymbol{p}_1 \boldsymbol{p}_2 \boldsymbol{p}_3 \boldsymbol{p}_4} \mathrm{e}^{\mathrm{i}(-\boldsymbol{p}_1 \cdot \boldsymbol{x} - \boldsymbol{p}_2 \cdot \boldsymbol{y} + \boldsymbol{p}_3 \cdot \boldsymbol{y} + \boldsymbol{p}_4 \cdot \boldsymbol{x})} \hat{a}^\dagger_{\boldsymbol{p}_1} \hat{a}^\dagger_{\boldsymbol{p}_2} V(\boldsymbol{x} - \boldsymbol{y}) \hat{a}_{\boldsymbol{p}_3} \hat{a}_{\boldsymbol{p}_4} $$
Changement de variables et jeu sur les indices aboutissent à :
$$\hat{V} = \frac{1}{2} \sum_{\boldsymbol{p}_1 \boldsymbol{p}_2 \boldsymbol{q}} \tilde{V}_{\boldsymbol{q}} \,\hat{a}^\dagger_{\boldsymbol{p}_1 + \boldsymbol{q}} \hat{a}^\dagger_{\boldsymbol{p}_2 - \boldsymbol{q}} \hat{a}_{\boldsymbol{p}_2} \hat{a}_{\boldsymbol{p}_1}$$
où $\tilde{V}_\boldsymbol{q}$ est la transformée de Fourier du potentiel.
La formule peut s’interpréter comme une diffusion dans l’espace des impulsions qui se représente conventionnellement par un dessin appelé diagramme de Feynman.
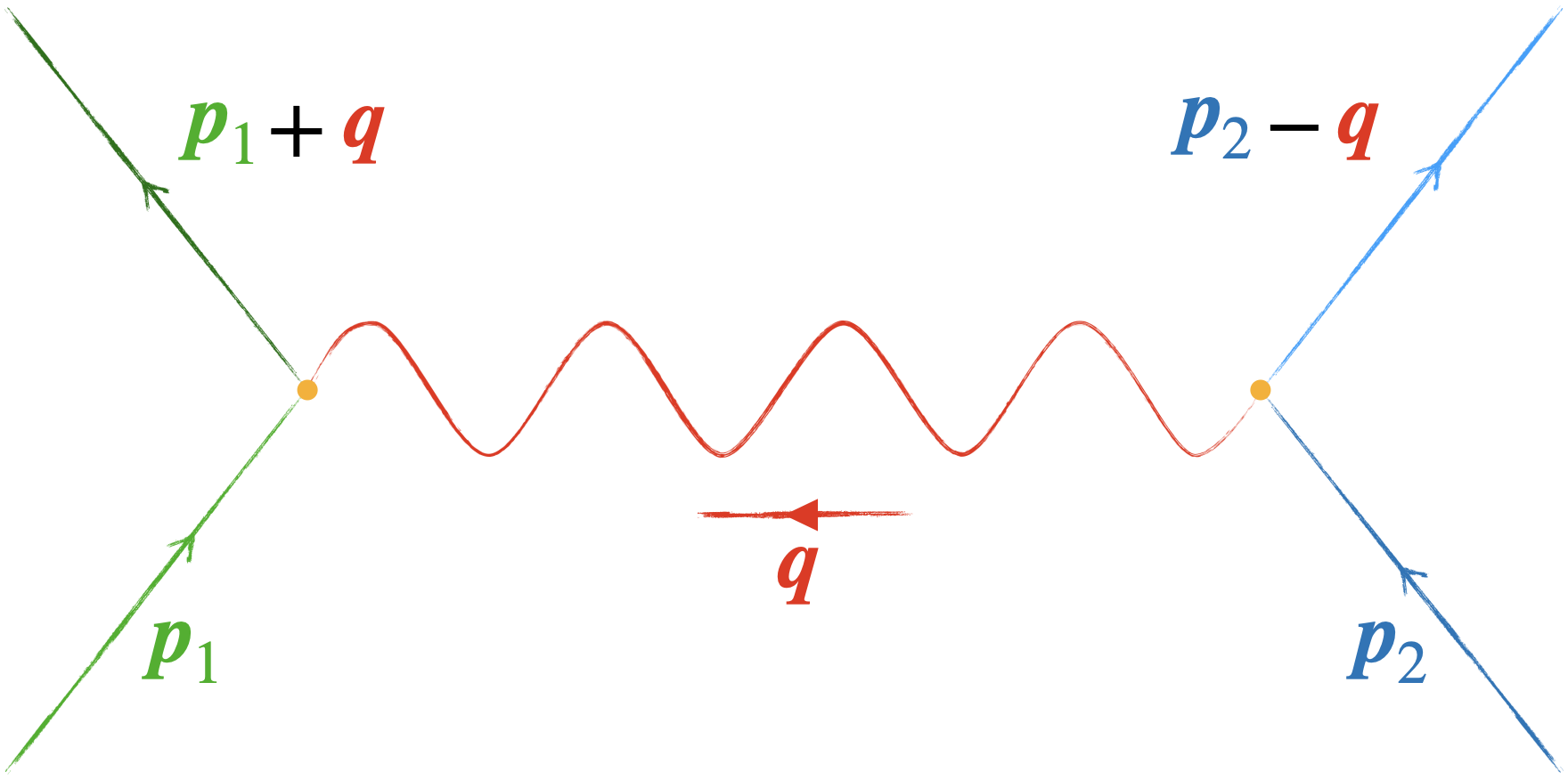
Une particule arrive avec une impulsion $\boldsymbol{p}_2$, émet une particule porteuse de force d’impulsion $\boldsymbol{q}$, réduisant ainsi son impulsion finale à $\boldsymbol{p}_2-\boldsymbol{q}$. La particule porteuse de force est absorbée par une autre particule dont l’impulsion passe alors de $\boldsymbol{p}_1$ à $\boldsymbol{p}_1+\boldsymbol{q}$. On constate que l’impulsion est conservée aux points de croisement du diagramme.
Pour réussir à évaluer l’énergie facilement, l’idée est de transformer toutes les combinaisons d’opérateurs en opérateurs nombre. Mais on se heurte à la non diagonalité du potentiel (les problèmes impliquant une énergie potentielle ne peuvent généralement pas être résolus de manière exacte). Malgré cela, le potentiel à deux particules peut nous mener à des richesses physiques insoupçonnées (magnétisme, superfluidité, supraconductivité,…).
Modèle de Hubbard
Le modèle de Hubbard est central en matière condensée. Il permet de capturer les implications physiques de la compétition entre énergie cinétique (qui favorise la délocalisation des électrons) et énergie potentielle (qui favorise leur localisation).
L’Hamiltonien du modèle de Hubbard est construit à partir de nos deux ingrédients précédents : l’Hamiltonien du modèle de liaisons fortes pour modéliser l’énergie cinétique et le potentiel à deux particules pour modéliser les interactions electron-electron :
$$\hat{H} = \sum_{ij} \left(-t_{ij} \hat{c}^\dagger_i \hat{c}_j\right) + \frac{1}{2} \sum_{ijkl} \hat{c}^\dagger_i \hat{c}^\dagger_j V_{ijkl} \hat{c}_k \hat{c}_l$$
Et comme les électrons possèdent un spin $\sigma$ qui peut pointer soit vers le haut ($|\uparrow\rangle$), soit vers le bas ($|\downarrow\rangle$), l’Hamiltonien devient :
$$\hat{H} = \sum_{ij\sigma} (-t_{ij}) \hat{c}^\dagger_{i\sigma} \hat{c}_{j\sigma} + \frac{1}{2} \sum_{ijkl\sigma\sigma’} \hat{c}^\dagger_{i\sigma} \hat{c}^\dagger_{j\sigma’} V_{ijkl} \hat{c}_{k\sigma’} \hat{c}_{l\sigma}$$
On suppose ici que les spins ne peuvent pas basculer. Comme l’interaction entre électrons vient de l’interaction de Coulomb, elle est indépendante de l’orientation du spin. Mais pour simplifier, on supposera que l’interaction coulombienne n’est notable que lorsque les électrons sont sur le même site. Les électrons interagissent donc via une énergie potentielle constante $U=V_{iiii}$. Mais comme le principe de Pauli impose que deux électrons sur le même site aient des spins opposés, l’Hamiltonien devient :
$$\hat{H} = \sum_{ij\sigma} (-t_{ij}) \hat{c}^\dagger_{i\sigma} \hat{c}_{j\sigma} + U \sum_i \hat{n}_{i\uparrow} \hat{n}_{i\downarrow}$$
Bien que simple d’allure, obtenir les états propres est souvent une tâche complexe et ceux-ci sont généralement fortement corrélés.
Simplifions à l’extrême avec un réseau de seulement deux sites, et un seul électron avec un spin haut $|\uparrow\rangle$. L’électron peut être soit sur le premier site, ce que l’on note $|\uparrow,0\rangle$ (spin haut sur le site 1, rien sur le site 2), soit sur le second $|0,\uparrow\rangle$ (rien sur le site 1, spin haut sur le site 2).
Un état général est une combinaison de ces deux états $|\psi\rangle = a|\uparrow,0\rangle+b|0,\uparrow\rangle$ et l’Hamiltonien de Hubbard peut s’écrire dans cette base :
$ \displaystyle \hat{H} = \begin{pmatrix} 0 & -t \\ -t & 0 \end{pmatrix} $
En diagonalisant, on obtient un état fondamental $|\psi\rangle=\frac{1}{\sqrt{2}}(|\uparrow,0\rangle+|0,\uparrow\rangle )$ pour une énergie $E=-t$, et un état excité $|\psi\rangle=\frac{1}{\sqrt{2}}(|\uparrow,0\rangle-|0,\uparrow\rangle )$ pour une énergie $E=t$.
Ajoutons un électron dans le système. S’il a le même spin, la solution est simplement $|\uparrow,\uparrow\rangle$ et l’énergie associée est $E=0$ (pas d’interaction possible puisque les deux électrons ne peuvent pas occuper le même site et ils ne peuvent pas sauter d’un site à l’autre, ils sont bloqués).
Montrons-le par le calcul :
Pour la partie potentiel, on obtient bien 0 puisque $U (\hat{n}_{1\uparrow} \hat{n}_{1\downarrow}+\hat{n}_{2\uparrow} \hat{n}_{2\downarrow})|\uparrow,\uparrow\rangle=U(1\times 0+1\times 0)|\uparrow,\uparrow\rangle = 0$ (puisque l'opérateur qui compte les spins bas trouve toujours zéro).Et pour la partie cinétique, on ne garde que les termes de spin haut de l'Hamiltonien : $-t (\hat{c}^\dagger_{1\uparrow} \hat{c}_{2\uparrow}+\hat{c}^\dagger_{2\uparrow} \hat{c}_{1\uparrow})$. Et on réécrit $|\uparrow,\uparrow\rangle$ comme $\hat{c}^\dagger_{1\uparrow}\hat{c}^\dagger_{2\uparrow}|0\rangle$.
$-t (\hat{c}^\dagger_{1\uparrow} \hat{c}_{2\uparrow}+\hat{c}^\dagger_{2\uparrow} \hat{c}_{1\uparrow})\hat{c}^\dagger_{1\uparrow}\hat{c}^\dagger_{2\uparrow}|0\rangle=-t \hat{c}^\dagger_{1\uparrow} \hat{c}_{2\uparrow}\hat{c}^\dagger_{1\uparrow}\hat{c}^\dagger_{2\uparrow}|0\rangle-t\hat{c}^\dagger_{2\uparrow} \hat{c}_{1\uparrow}\hat{c}^\dagger_{1\uparrow}\hat{c}^\dagger_{2\uparrow}|0\rangle=t \hat{c}^\dagger_{1\uparrow} \hat{c}_{2\uparrow}\hat{c}^\dagger_{2\uparrow}\hat{c}^\dagger_{1\uparrow}|0\rangle-t\hat{c}^\dagger_{2\uparrow} \hat{c}_{1\uparrow}\hat{c}^\dagger_{1\uparrow}\hat{c}^\dagger_{2\uparrow}|0\rangle=t \hat{c}^\dagger_{1\uparrow}(1-\hat{n}_{2\uparrow})\hat{c}^\dagger_{1\uparrow}|0\rangle-t\hat{c}^\dagger_{2\uparrow}(1-\hat{n}_{1\uparrow})\hat{c}^\dagger_{2\uparrow}|0\rangle = t \cancel{\hat{c}^\dagger_{1\uparrow} \hat{c}^\dagger_{1\uparrow} }|0\rangle - t\hat{c}^\dagger_{1\uparrow}\cancel{\hat{n}_{2\uparrow}|\uparrow,0\rangle}- t\cancel{\hat{c}^\dagger_{2\uparrow}\hat{c}^\dagger_{2\uparrow}}|0\rangle+t\hat{c}^\dagger_{2\uparrow}\cancel{\hat{n}_{1\uparrow}|0,\uparrow\rangle}=0$
S’ils sont de spins opposés, une base possible est $\{|\uparrow\downarrow,0\rangle,|\uparrow,\downarrow\rangle,|\downarrow,\uparrow\rangle,|0,\uparrow\downarrow\rangle\}$. Et dans cette base, l’Hamiltonien de Hubbard s’écrit :
$ \displaystyle \hat{H} = \begin{pmatrix} U & -t & t & 0 \\ -t & 0 & 0 & -t \\ t & 0 & 0 & t \\ 0 & -t & t & U \end{pmatrix} $
Détaillons juste l'action de l'Hamiltonien sur $|\uparrow\downarrow,0\rangle$ pour s'en convaincre :
Terme potentiel : $U \hat{n}_{1\uparrow}\hat{n}_{1\downarrow}|\uparrow\downarrow,0\rangle = U\times 1\times 1=U$ et $U \hat{n}_{2\uparrow}\hat{n}_{2\downarrow}|\uparrow\downarrow,0\rangle = U\times 0\times 0=0$ (puisque l’opérateur $\hat{n}$ ne fait que compter le nombres de particules dans un site donné).
Terme cinétique : comme $i$ et $j$ doivent être différents, on a 4 termes dans la somme $(-t) \hat{c}^\dagger_{1\uparrow} \hat{c}_{2\uparrow}+(-t) \hat{c}^\dagger_{2\uparrow} \hat{c}_{1\uparrow}+(-t) \hat{c}^\dagger_{1\downarrow} \hat{c}_{2\downarrow}+(-t) \hat{c}^\dagger_{2\downarrow} \hat{c}_{1\downarrow}$.
Seuls les deux termes contenant un opérateur d’annihilation sur le site 1 ne donneront pas un résultat nul. Il nous reste $-t(\hat{c}^\dagger_{2\uparrow} \hat{c}_{1\uparrow} +\hat{c}^\dagger_{2\downarrow} \hat{c}_{1\downarrow})$.
Appliquons cette somme d’opérateurs à $|\uparrow\downarrow,0\rangle$ qu’on peut aussi écrire $\hat{c}^\dagger_{1\uparrow}\hat{c}^\dagger_{1\downarrow}|0\rangle$.
Le permier terme nous donne $-t\hat{c}^\dagger_{2\uparrow} \hat{c}_{1\uparrow} \hat{c}^\dagger_{1\uparrow}\hat{c}^\dagger_{1\downarrow}|0\rangle=-t\hat{c}^\dagger_{2\uparrow} (1-\hat{n}_{1\uparrow})\hat{c}^\dagger_{1\downarrow}|0\rangle=-t\hat{c}^\dagger_{2\uparrow}\hat{c}^\dagger_{1\downarrow}|0\rangle+t\hat{c}^\dagger_{2\uparrow} \cancel{\hat{n}_{1\uparrow}|\downarrow,0\rangle}=-t\hat{c}^\dagger_{2\uparrow}|\downarrow,0\rangle=t|\downarrow,\uparrow\rangle$. Le dernier changement de signe venant du fait qu’il y ait déjà un fermion à gauche de celui créé dans l’état 2 ($(-1)^{n_1+n_2+\cdots+n_{i-1}}=(-1)^1=-1$).
Et le deuxième terme donne $-t\hat{c}^\dagger_{2\downarrow} \hat{c}_{1\downarrow}\hat{c}^\dagger_{1\uparrow}\hat{c}^\dagger_{1\downarrow}|0\rangle=t\hat{c}^\dagger_{2\downarrow} \hat{c}_{1\downarrow}\hat{c}^\dagger_{1\downarrow}\hat{c}^\dagger_{1\uparrow}|0\rangle=t\hat{c}^\dagger_{2\downarrow} (1-\hat{n}_{1\downarrow})\hat{c}^\dagger_{1\uparrow}|0\rangle=t\hat{c}^\dagger_{2\downarrow}\hat{c}^\dagger_{1\uparrow}|0\rangle-t\hat{c}^\dagger_{2\downarrow}\cancel{\hat{n}_{1\downarrow}|\uparrow,0\rangle}=-t|\uparrow,\downarrow\rangle$.
La matrice peut se diagonaliser et l’état fondamental s’écrit $|\psi\rangle = N(|\uparrow\downarrow,0\rangle+W|\uparrow,\downarrow\rangle-W|\downarrow,\uparrow\rangle+|0,\uparrow\downarrow\rangle)$ où $N$ est une constante de normalisation et $W=\frac{U}{4t}+\frac{1}{4t}\sqrt{U^2+16t^2}$ pour une énergie $E=\frac{U}{2}-\frac{1}{2}\sqrt{U^2+16t^2}$. C’est déjà un résultat étonament complexe pour un système si simple (deux électrons sur deux sites)…
On a découvert jusqu’ici comment des systèmes variés peuvent se réduire à un simple jeu d’oscillateurs harmoniques, chacun décrivant un certain mode normal du système. Et chacun de ces modes normaux peut-être vu comme un état d’impulsion pour des particules identiques sans interaction. Le nombre de particules correspond alors au nombre d’excitations quantifiées du mode. Et on a défini des opérateurs qui peuvent créer et annihiler ces particules.
Les modèles considérés se restreignaient à des réseaux discrets adaptés à la physique de la matière condensée. Dans le prochain chapitre, on va généraliser au continu.