Théorie quantique des champs – Partie 0
Notes de lecture du livre Quantum field theory for the gifted amateur de Thomas Lancaster et Stephen Blundell.
Lagrangien et principe de moindre action
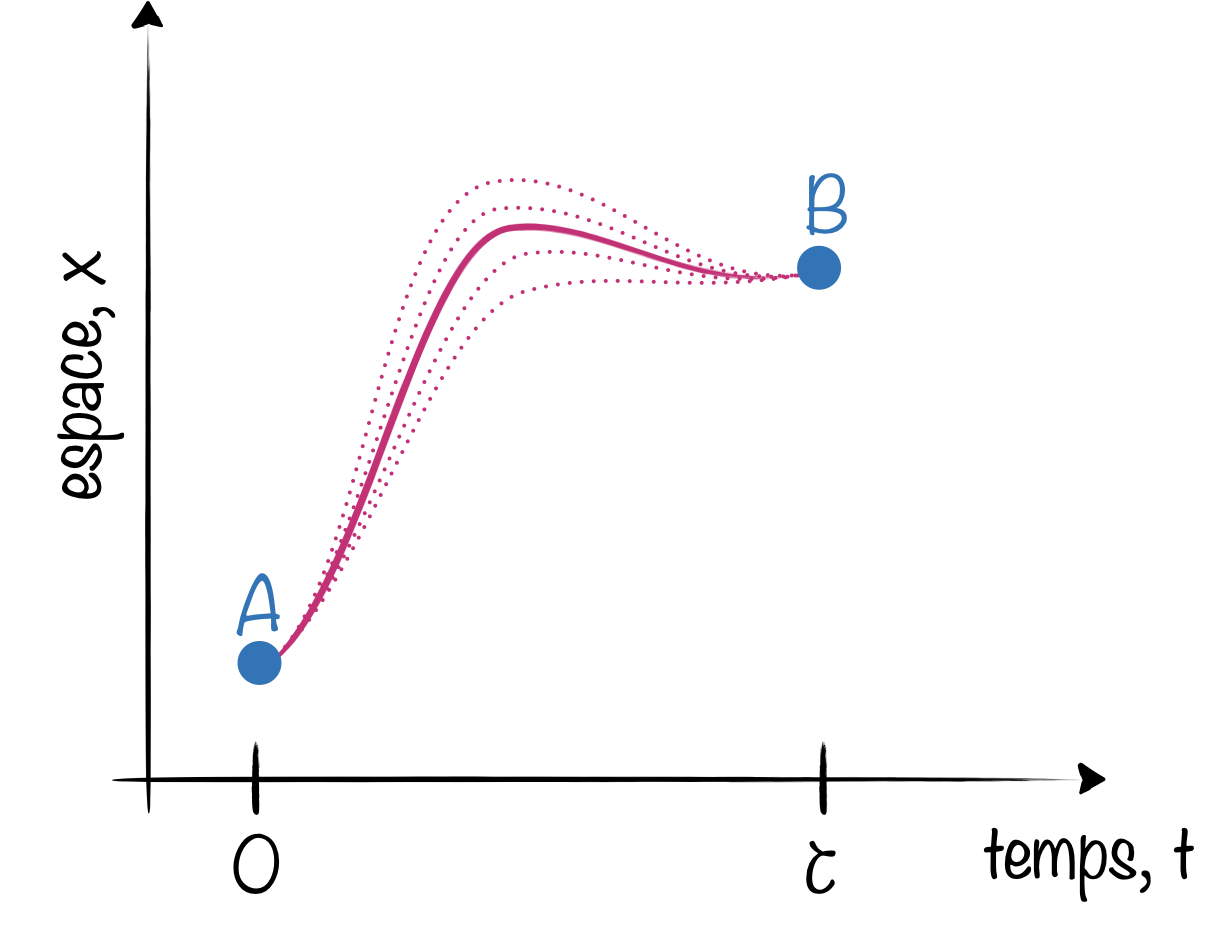
La détermination de la trajectoire $x(t)$ d’une particule entre A et B par intégration de la 2e loi de Newton, $F=m\ddot{x}$, ne cadre pas avec les enseignements de la mécanique quantique. Car si on peut bien mesurer la particule en A à $t=0$ et en B à $t=\tau$, un voile impénétrable nous empèche de savoir précisément ce qui s’est passé entre les deux. Une équation différentielle ne semble donc pas un point de départ prometteur pour calculer $x(t)$…
Concentrons-nous sur les variations de l’énergie cinétique $T$ et l’énergie potentielle $V$ le long de la trajectoire. L’énergie totale $E=T+V$ doit être une constante du mouvement de la particule mais l’équilibre entre les deux types d’énergie peut varier.
Notons $\displaystyle\bar{T}=\frac{1}{\tau}\int_0^\tau\frac{1}{2}m[\dot{x}(t)]^2 dt$ l’énergie cinétique moyenne sur la trajectoire et $\displaystyle\bar{V}=\frac{1}{\tau}\int_0^\tau V[x(t)] dt$, l’énergie potentielle moyenne. On a bien sûr $E=\bar{E}=\bar{T}+\bar{V}$.
Mathématiquement, $\bar{T}$ et $\bar{V}$ sont des fonctionnelles. Là où des fonctions se nourrissent de nombres pour produire des nombres, les fonctionnelles produisent des nombres à partir de fonctions ($\bar{T}$ produit un nombre à partir de $\dot{x}(t)$ et $\bar{V}$ à partir de $x(t)$).
La dérivée fonctionnelle de $F[f(x)]$ nous dit comment le nombre produit par la fonctionnelle varie lorsqu’on change légèrement la fonction $f(x)$ qu’elle machouille :
Dérivées fonctionnelles utilisées dans la suite :
- $F[f]=\int_a^b g[f(x)]\mathrm{d}x$ avec $g'=\mathrm{d}g/\mathrm{d}f$
$$ \begin{aligned} \frac{\delta F[f]}{\delta f(x_0)}&=\lim_{\epsilon \to 0}\frac{1}{\epsilon}\left[\int g[f(x)+\epsilon \delta(x-x_0)]dx-\int g[f(x)]\mathrm{d}x\right]\\\\ &=\lim_{\epsilon \to 0}\frac{1}{\epsilon}\left[\int (g[f(x)]+\epsilon\delta(x-x_0)g'[f(x)])\mathrm{d}x - \int g[f(x)]\mathrm{d}x\right]\\\\ &=\int \delta(x-x_0) g'[f(x)] \mathrm{d}x\\\\ &= g'[f(x_0)] \end{aligned} $$
On détermine ainsi que $\displaystyle \frac{\delta \bar{V}[x]}{\delta x(t)}=\frac{1}{\tau}V’[x(t)]$.
-
$F[f]=\int g(f’)\mathrm{d}y$ avec $f’=\mathrm{d}f/\mathrm{d}y$
$$\frac{\delta F[f]}{\delta f(x)}=\lim_{\epsilon \to 0}\frac{1}{\epsilon}\left[\int dy \,g\!\left( \frac{\partial}{\partial y}[f(y)+\epsilon \delta(y-x)]\right) - \int dy \,g\!\left(\frac{\partial f}{\partial y}\right)\right]$$Par un développement de Taylor au premier ordre, on obtient :
$$g\left(\frac{\partial}{\partial y}[f(y)+\epsilon\delta(y-x)]\right)=g(f'+\epsilon\delta'(y-x))\approx g(f')+\epsilon\delta'(y-x)\frac{\mathrm{d}g(f')}{\mathrm{d} f'}$$On aboutit à :
$$\frac{\delta F[f]}{\delta f(x)}=\int \mathrm{d}y \delta'(y-x)\frac{\mathrm{d}g(f')}{\mathrm{d} f'}$$On utilise alors une intégration par partie :$$\int \mathrm{d}y\, \delta'(y-x)\frac{\mathrm{d}g(f')}{\mathrm{d} f'}=\left[\delta(y-x)\frac{\mathrm{d}g(f')}{\mathrm{d} f'}\right]-\int \mathrm{d}y \,\delta(y-x)\frac{\mathrm{d}}{\mathrm{d} y}\left(\frac{\mathrm{d}g(f')}{\mathrm{d}f'}\right)$$Si $x$ se balade sur l'intervalle d'intégration, le terme entre crochets est de mesure nulle et on obtient finalement :$$\frac{\delta F[f]}{\delta f(x)}=-\frac{\mathrm{d}}{\mathrm{d} x}\left(\frac{\mathrm{d}g(f’)}{\mathrm{d}f’}\right)$$
On détermine ainsi que $\displaystyle \frac{\delta \bar{T}[x]}{\delta x(t)}=-\frac{m\ddot{x}}{\tau}$.
D’autre part, si on a $F[\phi]=\int\left(\frac{\partial\phi}{\partial y}\right)^2\mathrm{d}y$, on obtient $\displaystyle \frac{\delta F[\phi]}{\delta\phi(x)}=-2\frac{\partial^2\phi}{\partial x^2}$.
Résultat qui se généralise à 3 dimensions pour donner un truc plutôt utile :
Si $\displaystyle I=\int(\nabla\phi)^2\mathrm{d}^3 x$, alors $\displaystyle\frac{\delta I}{\delta\phi}=-2\nabla^2\phi$.
On peut maintenant vérifier comment $\bar{T}$ et $\bar{V}$ varient lorsque la trajectoire $x(t)$ est un peu modifiée :
Or d’après la 2e loi de Newton, la trajectoire classique correspond à $m\ddot{x}=-dV/dx$ et d’après ce qui précède, cela entraîne que $\displaystyle \frac{\delta \bar{V}[x]}{\delta x(t)}=\frac{\delta \bar{T}[x]}{\delta x(t)}$.
On en conclut que pour une légère déviation autour de la trajectoire classique, l’énergie potentielle moyenne et l’énergie cinétique moyenne vont varier ensemble (généralement augmenter) et de la même valeur !
Cela peut se réécrire $\displaystyle \frac{\delta }{\delta x(t)}(\bar{T}[x]- \bar{V}[x])=0$.
La différence entre les deux énergies moyennes est stationnaire près de la trajectoire classique.
On décide alors de donner un nom à cette différence entre énergie cinétique et potentielle : le lagrangien $L$.
L’intégrale du lagrangien sur le temps définit l’action $S$.
Ces deux nouvelles grandeurs vont nous permettre de réécrire de manière synthétique ce qu’on a découvert jusque-là.
$\displaystyle S=\int_0^\tau(T-V)\mathrm{d}t = \tau(\bar{T}[x]-\bar{V}[x])$, et donc
C’est le principe de moindre action de Hamilton.
Équations d’Euler-Lagrange :
Le lagrangien $L$ peut s’écrire comme une fonction à la fois de la position et de la vitesse $L(x(t),\dot{x}(t))$. Le principe de moindre action donne alors :
Démonstration :
On introduit aussi la densité lagrangienne $\mathcal{L}$ :
$$ S=\int \mathscr{d}t\,\mathscr{d}x\,\mathcal{L} $$
Plaçons-nous désormais dans un cadre relativiste : le lagrangien dépend maintenant d’une fonction $\phi(x)$ où $x$ est un point de l’espace-temps dont la dérivée est le 4-vecteur $\partial_\mu\phi$.
L’action devient :
$$S=\int \mathrm{d}^4 x\mathcal{L}(\phi,\partial_\mu\phi)$$
Le principe de moindre action fournit maintenant une version quadrivectorielle des équations d’Euler-Lagrange :
Le principe de moindre action tire sa justification de la mécanique quantique où les particules ne sont plus des particules mais des ondes. La particule allant d’un point A à un point B en empruntant toutes les trajectoires possibles (jusqu’aux plus saugrenues) devient donc une onde affublée d’un facteur de phase $\mathrm{e}^{\mathrm{i}S/\hbar}$ où $S$ est l’action. Une action stationnaire correspond alors à une phase stationnaire.
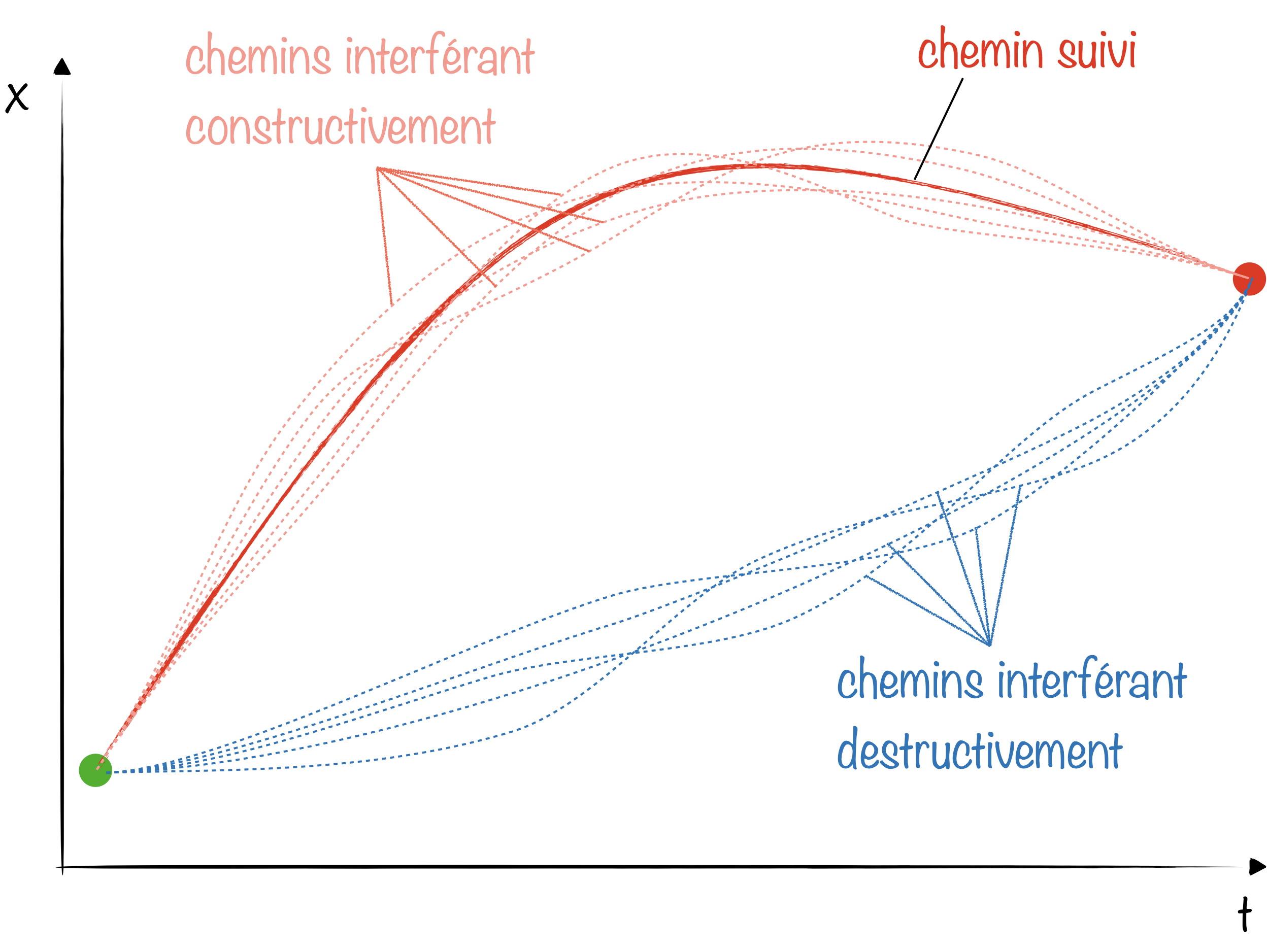
Lorsqu’on se retrouve à sommer sur toutes les trajectoires possibles, les différents termes vont interférer. L’interférence sera destructive dans l’immense majorité des cas, là où la phase fluctuera fortement d’une trajectoire à l’autre. Au contraire, la trajectoire minimisant l’action va émerger car toutes les trajectoires voisines auront des phases proches et interféreront constructivement.